This problem set is devoted to a variety of vector situations and coordinates for evaluation.
Problem 1
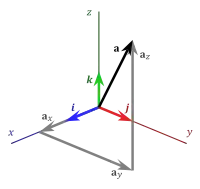
For standard basis, or unit, vectors (i, j, k) and vector components of a (ax, ay, az), what are the right ascension, declination, and value of a:
If the x-axis is the longitude of the Greenwich meridian, and ax equals ay, then RA equals?
If ax equals ay equals az, then the declination is?
The value of a is given by?
Problem 2

For standard basis, or unit, vectors (i, j, k) and vector components of a (ax, ay, az), what are the right ascension, declination, and value of a:
for ax equals ay equals az
If the x-axis is the longitude of the Greenwich meridian, and the object is at ax and 2ay, then RA equals?
ax and 2ay and 3az, then the declination is?
The value of a is given by?
Problem 3

For standard basis, or unit, vectors (i, j, k) and vector components of a (ax, ay, az), what are the right ascension, declination, and value of a:
for ax equals ay equals az
If the x-axis is the longitude of the Greenwich meridian, and the object is at 3ax and 4ay, then RA equals?
3ax and 4ay and 5az, then the declination is?
The value of a is given by?
Problem 4

For standard basis, or unit, vectors (i, j, k) and vector components of a (ax, ay, az), what are the right ascension, declination, and value of a:
for ax equals 2ay equals 3az
If the x-axis is the longitude of the Greenwich meridian, and the object is at 3ax and 4ay, then RA equals?
3ax and 4ay and 5az, then the declination is?
The value of a is given by?
Problem 5
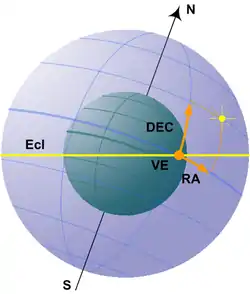
An object has RA 10h 10m 10s Dec -20° 20' 20" and r = 23 lyrs.
What are ax, ay, and az?
What are ℓ and b?
What are the ecliptic longitude and latitude?
What are J1855 and B1855?
What are J2100 and B2100?
Problem 6

An object has coordinates: 125.678 -85.678 and r = 110 pc.
What are RA and Dec?
What are ax, ay, and az?
What are ℓ and b?
What are the ecliptic longitude and latitude?
What are J1800 and B1800?
What are J2075 and B2075?
Problem 7

For standard basis, or unit, vectors (i, j, k) and vector components of a (ax, ay, az), for ax equals 2ay equals 3az:
If the x-axis is the longitude of the Greenwich meridian, and the object is at a = 3ax and b = 4ay, then what is
Problem 8

Standard basis, or unit, vectors are (i, j, k) for vector components of a (ax, ay, az).
Let ax equal 3ay equal 4az.
What are
If a = [5a_x, 6a_y, 7a_z] and b = [8a_x, 9a_y, 10a_z], then
Hypotheses
- The square root of negative one is not needed in vector space.
See also
External links
- Bing Advanced search
- Google Books
- Google scholar Advanced Scholar Search
- International Astronomical Union
- JSTOR
- Lycos search
- NASA/IPAC Extragalactic Database - NED
- NASA's National Space Science Data Center
- Office of Scientific & Technical Information
- Questia - The Online Library of Books and Journals
- SAGE journals online
- The SAO/NASA Astrophysics Data System
- Scirus for scientific information only advanced search
- SDSS Quick Look tool: SkyServer
- SIMBAD Astronomical Database
- SIMBAD Web interface, Harvard alternate
- Spacecraft Query at NASA
- SpringerLink
- Taylor & Francis Online
- Universal coordinate converter
- Wiley Online Library Advanced Search
- Yahoo Advanced Web Search
{{Charge ontology}}{{Flight resouces}}{{Principles of radiation astronomy}}
{{Repellor vehicle}}{{Technology resources}}