Notation: let the symbol represent change in.
Notation: let the symbol represent an infinitesimal change in.
Notation: let the symbol represent an infinitesimal change in one of more than one.
Def. significant "change in or effect on a situation or state"[1] or a "result of a subtraction; sometimes the absolute value of this result"[1] is called a difference.
Def. a result of an "operation of deducing one function from another according to some fixed law"[2] is called a derivative.
Let
be a function where values of may be any real number and values resulting in are also any real number.
- is a small finite change in which when put into the function produces a .
These small changes can be manipulated with the operations of arithmetic: addition (), subtraction (), multiplication (), and division ().
Dividing by and taking the limit as → 0, produces the slope of a line tangent to f(x) at the point x.
For example,
as and go towards zero,
This ratio is called the derivative.
Let
then
where z is held constant and
where x is held contstant.
Notation: let the symbol be the gradient, i.e., derivatives for multivariable functions.
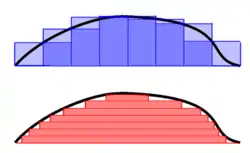
For
the area under the curve shown in the diagram at right is the light purple rectangle plus the dark purple rectangle in the top figure
Any particular individual rectangle for a sum of rectangular areas is
The approximate area under the curve is the sum of all the individual (i) areas from i = 0 to as many as the area needed (n):
Notation: let the symbol represent the integral.
This can be within a finite interval [a,b]
when i = 0 the integral is evaluated at and i = n the integral is evaluated at . Or, an indefinite integral (without notation on the integral symbol) as n goes to infinity and i = 0 is the integral evaluated at x = 0.
Def. a branch of mathematics that deals with the finding and properties of infinitesimal differences or changes is called a calculus.
Calculus focuses on limits, functions, derivatives, integrals, and infinite series.
"Although calculus (in the sense of analysis) is usually synonymous with infinitesimal calculus, not all historical formulations have relied on infinitesimals (infinitely small numbers that are nevertheless not zero)."[3]
References
- 1 2 difference. San Francisco, California: Wikimedia Foundation, Inc. 28 May 2015. Retrieved 2015-06-25.
- ↑ Poccil (13 January 2015). derivation. San Francisco, California: Wikimedia Foundation, Inc. Retrieved 2015-06-25.
- ↑ infinitesimal calculus. San Francisco, California: Wikimedia Foundation, Inc. September 19, 2012. Retrieved 2013-01-31.
External links
{{Reasoning resources}}