Correlation
In statistics and probability theory, correlation is how similar two sets of data are.[1] This relationship means that if one set of data changes, the other will change as well (at least more commonly than if it were up to pure chance).
Correlation does not always mean that one causes the other. In fact, it is very possible that there is a third factor involved. Correlation can have one of two directions: Positive or negative. If it is positive, then the two sets go up together. If it is negative, then one goes up while the other goes down. Lots of different measurements of correlation are used for different situations. For example, on a scatter graph, people draw a line of best fit to show the direction of the correlation.
Correlation can be measured through correlation coefficients. The most common correlation coefficients are Pearson correlation coefficient and Spearman's rank correlation.
Correlation is useful in real life. An example of correlation is the height of a parent and their children.
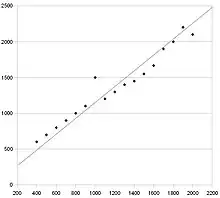
Explaining correlation
Strong and weak are words used to describe the strength of correlation. If there is strong correlation, then the points are all close together. If there is weak correlation, then the points are all spread apart. There are ways of making numbers show how strong the correlation is. These measurements are called correlation coefficients. The best known is the Pearson product-moment correlation coefficient, sometimes denoted by or its Greek equivalent .[2][3] You put in data into a formula, and it gives you a number between -1 and 1.[4] If the number is 1 or −1, then there is strong correlation. If the answer is 0, then there is no correlation. Another kind of correlation coefficient is Spearman's rank correlation coefficient.
Correlation vs causation
Correlation does not always mean that one thing causes the other (causation or causal relationship), because there might be something else that is at play.
For example, on hot days people buy ice cream, and people also go to the beach where some are attacked by sharks. There is a correlation between ice cream sales and shark attacks (they both go up as the temperature goes up in this case). But that ice cream sales go up does not mean ice cream sales cause (causation) more shark attacks or vice versa.[5] However, there is also a correlation between temperature and shark attacks, which are two things that actually do have a causal relationship; higher temperatures cause shark attacks, because they cause more people to go swimming.
This means that while checking for correlation can be (and often is) used to test if there could be causation (if there is causation, there will probably also be a correlation, at least if you look at enough data), it is not enough to prove that there definitely is causation. As in the ice cream example, it is also possible that the correlation is due to an additional factor – in statistics, this is called a confounding variable.
Because correlation alone does not prove causation, scientists, economists, etc. will test their ideas by creating isolated environments where only one factor is changed (if possible).
For example, when testing a new drug, doctors will try to find two groups of people that are very similar to each other in every possible way (e.g. age, sex, health conditions etc.), but only test the actual drug on one of the two groups. Afterwards they can check if they can find significant differences between the groups. Significance in statistics means that a difference or relationship is stronger than what might just be caused by pure chance. If they find such significant differences, they can be relatively sure that this is due to the drug, because they have made sure beforehand that there are no other factors that could cause such a difference between the groups.
However, politicians, salesmen, news outlets and others often erroneously suggest that a particular correlation implies causation. This may be due to ignorance or dishonesty. Thus, a news report may attract attention by saying that people who consume a particular product more often have a particular health problem, implying a causation that could be actually due to something else.
Another thing to keep in mind is that even if there is causation, just looking at the correlation alone does not tell us which direction it is in. For example if we look at how often people visit hospitals and how often people are sick, we will see a correlation that is, in this case, due to a causation. Yet, it would of course be wrong to conclude from this that going to the hospital causes people to be sick: The causation here is of course in the other direction, being sick is what causes people to go to the hospital. This is why it is always important to check if your interpretation of causality based on a correlation is plausible or not.
Related pages
References
- "Correlation and Causation - easily explained! | Data Basecamp". 2021-11-27. Retrieved 2022-07-01.
- "List of Probability and Statistics Symbols". Math Vault. 2020-04-26. Retrieved 2020-08-22.
- Even though it is called 'Pearson', it was first made by Francis Galton.
- Weisstein, Eric W. "Statistical Correlation". mathworld.wolfram.com. Retrieved 2020-08-22.
- "Ice cream and shark attacks". Big Think. 2019-02-21. Archived from the original on 2020-09-28. Retrieved 2020-08-22.
Further readings
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences. (3rd ed.) Hillsdale, NJ: Lawrence Erlbaum Associates.
- Oestreicher, J. & D. R. (February 26, 2015). Plague of Equals: A science thriller of international disease, politics and drug discovery. California: Omega Cat Press. p. 408. ISBN 978-0963175540.
Other websites
- Correlation Information – At StatisticalEngineering.com
- Statsoft Electronic Textbook Archived 2009-02-27 at the Wayback Machine
- Pearson's Correlation Coefficient – How to work it out it quickly
- Learning by Simulations – The spread of the correlation coefficient
- CorrMatr.c Archived 2007-12-04 at the Wayback Machine simple program for working out a correlation matrix
- Understanding Correlation Archived 2007-12-17 at the Wayback Machine – More beginner's information by a Hawaii professor