Bayesian inference
Bayesian inference (/ˈbeɪziən/ BAY-zee-ən or /ˈbeɪʒən/ BAY-zhən)[1] is a type of statistical inference. In Bayesian inference, evidence or information is available, Bayes' theorem is used to change (or update) the probability of a hypothesis. Bayesian inference uses a prior distribution to estimate posterior probabilities. Bayesian inference is an important to statistics, mathematical statistics, decision theory, and sequential analysis. Bayesian inference is used in science, engineering, philosophy, medicine, sport, and law.
| Part of a series on |
| Bayesian statistics |
|---|
| Posterior = Likelihood × Prior ÷ Evidence |
| Background |
|
| Model building |
|
| Posterior approximation |
|
| Estimators |
|
| Evidence approximation |
|
| Model evaluation |
|
Bayes' rule
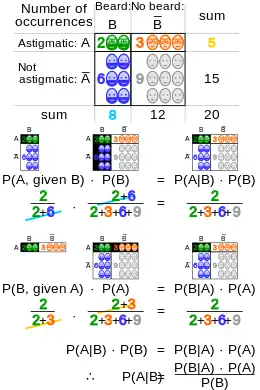
A geometric visualisation of Bayes' theorem. In the table, the values 2, 3, 6 and 9 give the relative weights of each corresponding condition and case. The figures denote the cells of the table involved in each metric, the probability being the fraction of each figure that is shaded. This shows that P(A|B) P(B) = P(B|A) P(A) i.e. P(A|B) = P(B|A) P(A)/P(B) . Similar reasoning can be used to show that P(¬A|B) = P(B|¬A) P(¬A)/P(B) etc.
| Satisfies hypothesis H | Violates hypothesis ¬H | Total | ||
|---|---|---|---|---|
| Has evidence E |
P(H|E)·P(E) = P(E|H)·P(H) | P(¬H|E)·P(E) = P(E|¬H)·P(¬H) | P(E) | |
| No evidence ¬E |
P(H|¬E)·P(¬E) = P(¬E|H)·P(H) | P(¬H|¬E)·P(¬E) = P(¬E|¬H)·P(¬H) | P(¬E) = 1−P(E) | |
| Total | P(H) | P(¬H) = 1−P(H) | 1 | |
Bayesian inference figures out the posterior probability from prior probability and the "likelihood function". The likelihood function comes from a statistical model of the data.
where
- is a hypothesis that is changed by data (or evidence). There are usually many hypotheses. The point of the test is to see which hypothesis is more likely.
- is the prior probability. It estimates the probability of a hypothesis before there is any evidence.
- is the evidence, or data. It is any new data that is found.
- is the posterior probability. This is what we want to know.
- is the likelihood function.
- is the marginal likelihood. It is the same for all possible hypotheses that are being tested. has to be greater than 0. If is 0, then you divide by zero.
Related pages
Further reading
- Vallverdu, Jordi (2016). Bayesians Versus Frequentists A Philosophical Debate on Statistical Reasoning. New York: Springer. ISBN 978-3-662-48638-2.
- Clayton, Aubrey (August 2021). Bernoulli's Fallacy: Statistical Illogic and the Crisis of Modern Science. Columbia University Press. ISBN 978-0-231-55335-3.
- Stone, JV (2013), "Bayes' Rule: A Tutorial Introduction to Bayesian Analysis", Download first chapter here, Sebtel Press, England.
- Dennis V. Lindley (2013). Understanding Uncertainty, Revised Edition (2nd ed.). John Wiley. ISBN 978-1-118-65012-7.
- Colin Howson & Peter Urbach (2005). Scientific Reasoning: The Bayesian Approach (3rd ed.). Open Court Publishing Company. ISBN 978-0-8126-9578-6.
- Berry, Donald A. (1996). Statistics: A Bayesian Perspective. Duxbury. ISBN 978-0-534-23476-8.
- Morris H. DeGroot & Mark J. Schervish (2002). Probability and Statistics (third ed.). Addison-Wesley. ISBN 978-0-201-52488-8.
- Bolstad, William M. (2007) Introduction to Bayesian Statistics: Second Edition, John Wiley ISBN 0-471-27020-2
- Winkler, Robert L (2003). Introduction to Bayesian Inference and Decision (2nd ed.). Probabilistic. ISBN 978-0-9647938-4-2. Updated classic textbook. Bayesian theory clearly presented.
- Lee, Peter M. Bayesian Statistics: An Introduction. Fourth Edition (2012), John Wiley ISBN 978-1-1183-3257-3
- Carlin, Bradley P. & Louis, Thomas A. (2008). Bayesian Methods for Data Analysis, Third Edition. Boca Raton, FL: Chapman and Hall/CRC. ISBN 978-1-58488-697-6.
- Gelman, Andrew; Carlin, John B.; Stern, Hal S.; Dunson, David B.; Vehtari, Aki; Rubin, Donald B. (2013). Bayesian Data Analysis, Third Edition. Chapman and Hall/CRC. ISBN 978-1-4398-4095-5.
- Berger, James O (1985). Statistical Decision Theory and Bayesian Analysis. Springer Series in Statistics (Second ed.). Springer-Verlag. Bibcode:1985sdtb.book.....B. ISBN 978-0-387-96098-2.
- Bernardo, José M.; Smith, Adrian F. M. (1994). Bayesian Theory. Wiley.
- DeGroot, Morris H., Optimal Statistical Decisions. Wiley Classics Library. 2004. (Originally published (1970) by McGraw-Hill.) ISBN 0-471-68029-X.
- Schervish, Mark J. (1995). Theory of statistics. Springer-Verlag. ISBN 978-0-387-94546-0.
- Jaynes, E. T. (1998). Probability Theory: The Logic of Science.
- O'Hagan, A. and Forster, J. (2003). Kendall's Advanced Theory of Statistics, Volume 2B: Bayesian Inference. Arnold, New York. ISBN 0-340-52922-9.
- Robert, Christian P (2007). The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation (paperback ed.). Springer. ISBN 978-0-387-71598-8.
- Pearl, Judea. (1988). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference, San Mateo, CA: Morgan Kaufmann.
- Pierre Bessière et al. (2013). "Bayesian Programming". CRC Press. ISBN 9781439880326
- Francisco J. Samaniego (2010). "A Comparison of the Bayesian and Frequentist Approaches to Estimation". Springer. New York, ISBN 978-1-4419-5940-9
References
Other websites
- Bayesian Statistics from Scholarpedia.
- Introduction to Bayesian probability from Queen Mary University of London
- Mathematical Notes on Bayesian Statistics and Markov Chain Monte Carlo
- Bayesian reading list Archived 2011-06-25 at the Wayback Machine, categorized and annotated by Tom Griffiths
- A. Hajek and S. Hartmann: Bayesian Epistemology, in: J. Dancy et al. (eds.), A Companion to Epistemology. Oxford: Blackwell 2010, 93–106.
- S. Hartmann and J. Sprenger: Bayesian Epistemology, in: S. Bernecker and D. Pritchard (eds.), Routledge Companion to Epistemology. London: Routledge 2010, 609–620.
- Stanford Encyclopedia of Philosophy: "Inductive Logic"
- Bayesian Confirmation Theory (PDF)
- Data, Uncertainty and Inference — Informal introduction with many examples, ebook (PDF) freely available at causaScientia
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.