| Great retrosnub icosidodecahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 92, E = 150 V = 60 (χ = 2) |
| Faces by sides | (20+60){3}+12{5/2} |
| Coxeter diagram | |
| Wythoff symbol | | 2 3/2 5/3 |
| Symmetry group | I, [5,3]+, 532 |
| Index references | U74, C90, W117 |
| Dual polyhedron | Great pentagrammic hexecontahedron |
| Vertex figure | 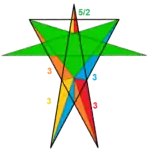 (34.5/2)/2 |
| Bowers acronym | Girsid |

In geometry, the great retrosnub icosidodecahedron or great inverted retrosnub icosidodecahedron is a nonconvex uniform polyhedron, indexed as U74. It has 92 faces (80 triangles and 12 pentagrams), 150 edges, and 60 vertices.[1] It is given a Schläfli symbol sr{3⁄2,5⁄3}.
Cartesian coordinates
Cartesian coordinates for the vertices of a great retrosnub icosidodecahedron are all the even permutations of
with an even number of plus signs, where
where is the golden ratio and ξ is the smaller positive real root of
Taking the odd permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph of the other one. Taking the odd permutations with an even number of plus signs or vice versa results in the same two figures rotated by 90 degrees.
The circumradius for unit edge length is
where x is the appropriate root of The four positive real roots of the sextic in R2,
are the circumradii of the snub dodecahedron (U29), great snub icosidodecahedron (U57), great inverted snub icosidodecahedron (U69), and great retrosnub icosidodecahedron (U74).
See also
References
- ↑ Maeder, Roman. "74: great retrosnub icosidodecahedron". MathConsult.
External links