Example 1: Circular Cylinder

Choose warping function

${\displaystyle \psi (x_{1},x_{2})=0}$

Equilibrium (${\displaystyle \nabla ^{2}{\psi }=0}$) is trivially satisfied.

The traction free BC is

${\displaystyle (0-x_{2}){\frac {dx_{2}}{ds}}-(0+x_{1}){\frac {dx_{1}}{ds}}=0~~~~\forall (x_{1},x_{2})\in \partial {\text{S}}}$

Integrating,

${\displaystyle x_{2}^{2}+x_{1}^{2}=c^{2}~~~~\forall (x_{1},x_{2})\in \partial {\text{S}}}$

where ${\displaystyle c}$ is a constant.

Hence, a circle satisfies traction-free BCs.

There is no warping of cross sections for circular cylinders

The torsion constant is

${\displaystyle {\tilde {J}}=\int _{S}(x_{1}^{2}+x_{2}^{2})dA=\int _{S}r^{2}dA=J}$

The twist per unit length is

${\displaystyle \alpha ={\frac {T}{\mu J}}}$

The non-zero stresses are

${\displaystyle \sigma _{13}=-\mu \alpha x_{2}~;~~\sigma _{23}=\mu \alpha x_{1}}$

The projected shear traction is

${\displaystyle \tau =\mu \alpha {\sqrt {(x_{1}^{2}+x_{2}^{2})}}=\mu \alpha r}$

Compare results from Mechanics of Materials solution

${\displaystyle \phi ={\frac {TL}{GJ}}~~\Rightarrow ~~\alpha ={\frac {T}{GJ}}}$

and

${\displaystyle \tau ={\frac {Tr}{J}}~~\Rightarrow ~~\tau =G\alpha r}$

Example 2: Elliptical Cylinder

Choose warping function

${\displaystyle \psi (x_{1},x_{2})=kx_{1}x_{2}\,}$

where ${\displaystyle k}$ is a constant.

Equilibrium (${\displaystyle \nabla ^{2}{\psi }=0}$) is satisfied.

The traction free BC is

${\displaystyle (kx_{2}-x_{2}){\frac {dx_{2}}{ds}}-(kx_{1}+x_{1}){\frac {dx_{1}}{ds}}=0~~~~\forall (x_{1},x_{2})\in \partial {\text{S}}}$

Integrating,

${\displaystyle x_{1}^{2}+{\frac {1-k}{1+k}}x_{2}^{2}=a^{2}~~~~\forall (x_{1},x_{2})\in \partial {\text{S}}}$

where ${\displaystyle a}$ is a constant.

This is the equation for an ellipse with major and minor axes ${\displaystyle a}$ and ${\displaystyle b}$, where

${\displaystyle b^{2}=\left({\frac {1+k}{1-k}}\right)a^{2}}$

The warping function is

${\displaystyle \psi =-\left({\frac {a^{2}-b^{2}}{a^{2}+b^{2}}}\right)x_{1}x_{2}}$

The torsion constant is

${\displaystyle {\tilde {J}}={\frac {2b^{2}}{a^{2}+b^{2}}}I_{2}+{\frac {2a^{2}}{a^{2}+b^{2}}}I_{1}={\frac {\pi a^{3}b^{3}}{a^{2}+b^{2}}}}$

where

${\displaystyle I_{1}=\int _{S}x_{1}^{2}dA={\frac {\pi ab^{3}}{4}}~~;~~I_{2}=\int _{S}x_{2}^{2}dA={\frac {\pi a^{3}b}{4}}}$

If you compare ${\displaystyle {\tilde {J}}}$ and ${\displaystyle J}$ for the ellipse, you will find that ${\displaystyle {\tilde {J}}<J}$. This implies that the torsional rigidity is less than that predicted with the assumption that plane sections remain plane.

The twist per unit length is

${\displaystyle \alpha ={\frac {(a^{2}+b^{2})T}{\mu \pi a^{3}b^{3}}}}$

The non-zero stresses are

${\displaystyle \sigma _{13}=-{\frac {2\mu \alpha a^{2}x_{2}}{a^{2}+b^{2}}}~~;~~\sigma _{23}=-{\frac {2\mu \alpha b^{2}x_{1}}{a^{2}+b^{2}}}}$

The projected shear traction is

${\displaystyle \tau ={\frac {2\mu \alpha }{a^{2}+b^{2}}}{\sqrt {b^{4}x_{1}^{2}+a^{4}x_{2}^{2}}}~~\Rightarrow ~~\tau _{\text{max}}={\frac {2\mu \alpha a^{2}b}{a^{2}+b^{2}}}~~(b<a)}$

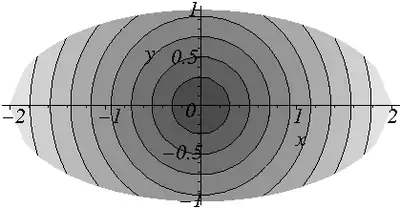Shear stresses in the cross section of an elliptical cylinder under torsion

For any torsion problem where ${\displaystyle \partial }$S is convex, the maximum projected shear traction occurs at the point on ${\displaystyle \partial }$S that is nearest the centroid of S

The displacement ${\displaystyle u_{3}}$ is

${\displaystyle u_{3}=-{\frac {(a^{2}-b^{2})Tx_{1}x_{2}}{\mu \pi a^{3}b^{3}}}}$

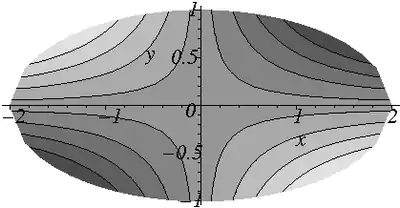Displacements (${\displaystyle u_{3}}$) in the cross section of an elliptical cylinder under torsion

Example 3: Rectangular Cylinder

In this case, the form of ${\displaystyle \psi }$ is not obvious and has to be derived from the traction-free BCs

${\displaystyle (\psi _{,1}-x_{2}){\hat {n}}_{1}+(\psi _{,2}+x_{1}){\hat {n}}_{2}=0~~~~\forall (x_{1},x_{2})\in \partial {\text{S}}}$

Suppose that ${\displaystyle 2a}$ and ${\displaystyle 2b}$ are the two sides of the rectangle, and ${\displaystyle a>b}$. Also ${\displaystyle a}$ is the side parallel to ${\displaystyle x_{1}}$ and ${\displaystyle b}$ is the side parallel to ${\displaystyle x_{2}}$. Then, the traction-free BCs are

${\displaystyle \psi _{,1}=x_{2}~~{\text{on}}~~x_{1}=\pm a~~,{\text{and}}~~\psi _{,2}=-x_{1}~~{\text{on}}~~x_{2}=\pm b}$

A suitable ${\displaystyle \psi }$ must satisfy these BCs and ${\displaystyle \nabla ^{2}{\psi }=0}$.

We can simplify the problem by a change of variable

${\displaystyle {\bar {\psi }}=x_{1}x_{2}-\psi }$

Then the equilibrium condition becomes

${\displaystyle \nabla ^{2}{\bar {\psi }}=0}$

The traction-free BCs become

${\displaystyle {\bar {\psi }}_{,1}=0~~{\text{on}}~~x_{1}=\pm a~~,{\text{and}}~~{\bar {\psi }}_{,2}=2x_{1}~~{\text{on}}~~x_{2}=\pm b}$

Let us assume that

${\displaystyle {\bar {\psi }}(x_{1},x_{2})=f(x_{1})g(x_{2})}$

Then,

${\displaystyle \nabla ^{2}{\bar {\psi }}={\bar {\psi }}_{,11}+{\bar {\psi }}_{,22}=f^{''}(x_{1})g(x_{2})+g^{''}(x_{2})f(x_{1})=0}$

or,

${\displaystyle {\frac {f^{''}(x_{1})}{f(x_{1})}}=-{\frac {g^{''}(x_{2})}{g(x_{2})}}=\eta }$

Case 1: ${\displaystyle \eta >0}$ or ${\displaystyle \eta =0}$

In both these cases, we get trivial values of ${\displaystyle C_{1}=C_{2}=0}$.

Membrane Analogy

The equations

${\displaystyle \nabla ^{2}{\phi }=-2\mu \alpha ~~\forall ~(x_{1},x_{2})\in {\text{S}}~~;~~~\phi =0~~\forall ~(x_{1},x_{2})\in \partial {\text{S}}}$

are similar to the equations that govern the displacement of a membrane that is stretched between the boundaries of the cross-sectional curve and loaded by an uniform normal pressure.

This analogy can be useful in estimating the location of the maximum shear stress and the torsional rigidity of a bar.

• The stress function is proportional to the displacement of the membrane from the plane of the cross-section.
• The stiffest cross-sections are those that allow the maximum volume to be developed between the deformed membrane and the plane of the cross-section for a given pressure.
• The shear stress is proportional to the slope of the membrane.

Example: Equilateral Triangle

Torsion of a cylinder with a triangular cross section

The equations of the three sides are

${\displaystyle {\begin{aligned}{\text{side}}~\partial S^{(1)}~:~~&f_{1}(x_{1},x_{2})=x_{1}-{\sqrt {3}}x_{2}+2a=0\\{\text{side}}~\partial S^{(2)}~:~~&f_{2}(x_{1},x_{2})=x_{1}+{\sqrt {3}}x_{2}+2a=0\\{\text{side}}~\partial S^{(3)}~:~~&f_{3}(x_{1},x_{2})=x_{1}-a=0\end{aligned}}}$

Let the Prandtl stress function be

${\displaystyle \phi =Cf_{1}f_{2}f_{3}}$

Clearly, ${\displaystyle \phi =0}$ at the boundary of the cross-section (which is what we need for solid cross sections).

Since, the traction-free boundary conditions are satisfied by ${\displaystyle \phi }$, all we have to do is satisfy the compatibility condition to get the value of ${\displaystyle C}$. If we can get a closed for solution for ${\displaystyle C}$, then the stresses derived from ${\displaystyle \phi }$ will satisfy equilibrium.

Expanding ${\displaystyle \phi }$ out,

${\displaystyle \phi =C(x_{1}-{\sqrt {3}}x_{2}+2a)(x_{1}+{\sqrt {3}}x_{2}+2a)(x_{1}-a)}$

Plugging into the compatibility condition

${\displaystyle \nabla ^{2}{\phi }=12Ca=-2\mu \alpha }$

Therefore,

${\displaystyle C=-{\frac {\mu \alpha }{6a}}}$

and the Prandtl stress function can be written as

${\displaystyle \phi =-{\frac {\mu \alpha }{6a}}(x_{1}^{3}+3ax_{1}^{2}+3ax_{2}^{2}-3x_{1}x_{2}^{2}-4a^{3})}$

The torque is given by

${\displaystyle T=2\int _{S}\phi dA=2\int _{-2a}^{a}\int _{-(x_{1}+2a)/{\sqrt {3}}}^{(x_{1}+2a)/{\sqrt {3}}}\phi dx_{2}dx_{1}={\frac {27}{5{\sqrt {3}}}}\mu \alpha a^{4}}$

Therefore, the torsion constant is

${\displaystyle {\tilde {J}}={\frac {27a^{4}}{5{\sqrt {3}}}}}$

The non-zero components of stress are

${\displaystyle {\begin{aligned}\sigma _{13}=\phi _{,2}&={\frac {\mu \alpha }{a}}(x_{1}-a)x_{2}\\\sigma _{23}=-\phi _{,1}&={\frac {\mu \alpha }{2a}}(x_{1}^{2}+2ax_{1}-x_{2}^{2})\end{aligned}}}$

The projected shear stress

${\displaystyle \tau ={\sqrt {\sigma _{13}^{2}+\sigma _{23}^{2}}}}$

is plotted below

Stresses in a cylinder with a triangular cross section under torsion

The maximum value occurs at the middle of the sides. For example, at ${\displaystyle (a,0)}$,

${\displaystyle \tau _{\text{max}}={\frac {3\mu \alpha a}{2}}}$

The out-of-plane displacements can be obtained by solving for the warping function ${\displaystyle \psi }$. For the equilateral triangle, after some algebra, we get

${\displaystyle u_{3}={\frac {\alpha x_{2}}{6a}}(3x_{1}^{2}-x_{2}^{2})}$

The displacement field is plotted below

Displacements ${\displaystyle u_{3}}$ in a cylinder with a triangular cross section.

Thin-walled Open Sections

Examples are I-beams, channel sections and turbine blades.

We assume that the length ${\displaystyle b}$ is much larger than the thickness ${\displaystyle t}$, and that ${\displaystyle t}$ does not vary rapidly with change along the length axis ${\displaystyle \xi }$.

Using the membrane analogy, we can neglect the curvature of the membrane in the ${\displaystyle \xi }$ direction, and the Poisson equation reduces to

${\displaystyle {\frac {d^{\phi }}{d\eta ^{2}}}=-2\mu \alpha }$

which has the solution

${\displaystyle \phi =\mu \alpha \left({\frac {t^{2}}{4}}-\eta ^{2}\right)}$

where ${\displaystyle \eta }$ is the coordinate along the thickness direction.

The stress field is

${\displaystyle \sigma _{3\xi }={\frac {\partial }{\partial }}{\phi }{\eta }=-e\mu \beta \eta ~~;~~~\sigma _{3\eta }=0}$

Thus, the maximum shear stress is

${\displaystyle \tau _{\text{max}}=\mu \beta t_{\text{max}}}$

Thin-walled Closed Sections

The Prandtl stress function ${\displaystyle \phi }$ can be approximated as a linear function between ${\displaystyle \phi _{1}}$ and ${\displaystyle 0}$ on the two adjacent boundaries.

The local shear stress is, therefore,

${\displaystyle \sigma _{3s}={\frac {\phi _{1}}{t}}}$

where ${\displaystyle s}$ is the parameterizing coordinate of the boundary curve of the cross-section and ${\displaystyle t}$ is the local wall thickness.

The value of ${\displaystyle \phi _{1}}$ can determined using

${\displaystyle \phi _{1}={\frac {2\mu \alpha A}{\oint _{S}{\frac {dS}{t}}}}}$

where ${\displaystyle A}$ is the area enclosed by the mean line between the inner and outer boundary.

The torque is approximately

${\displaystyle T=2A\phi _{1}}$