For more help with phasors visit Phasor algebra

Time average of the product of two signals

Here we multiply two signals with the same angular frequency but with different phases:

${\displaystyle I(t)=I_{0}\cos(\omega t+\phi _{i})={\tfrac {1}{2}}I_{0}\exp {i(\omega t+\phi _{i})}+cc}$

${\displaystyle V(t)=V_{0}\cos(\omega t+\phi _{v})={\tfrac {1}{2}}V_{0}\exp {i(\omega t+\phi _{v})}+cc}$,

where ${\displaystyle cc}$ denotes complex conjugate. For example,

${\displaystyle e^{i\theta }+cc=e^{i\theta }+e^{-i\theta }=2\cos \theta .}$

Define ${\displaystyle P=IV}$, and make the algebra easier to follow by defining two phases:

${\displaystyle \Phi _{I}=\omega t+\phi _{i},}$   and,   ${\displaystyle \Phi _{V}=\omega t+\phi _{v}}$.

Note that ${\displaystyle PV}$ is the product of two binomials, which yield four terms:

${\displaystyle IV={\tfrac {1}{4}}I_{0}V_{0}\left(e^{i\Phi _{I}}+e^{-i\Phi _{I}}\right)\left(e^{i\Phi _{V}}+e^{-i\Phi _{V}}\right)}$

When the two binomials are multiplied we obtain four terms. We group them according to whether they involve the sum or difference between the two phases, ${\displaystyle \Phi _{I}}$ and ${\displaystyle \Phi _{V}}$, because whether it is a sum or difference affects the time-dependence as follows:

${\displaystyle \Phi _{I}+\Phi _{V}=2\omega t+\phi _{i}+\phi _{v}}$

${\displaystyle \Phi _{I}-\Phi _{V}=\phi _{i}-\phi _{v}}$

These terms can be grouped into real and imaginary parts, expressed in terms of the sine and cosine functions:

${\displaystyle IV={\tfrac {1}{4}}I_{0}V_{0}{\Bigl [}\underbrace {e^{i(\Phi _{I}-\Phi _{V})}+e^{i(\Phi _{V}-\Phi _{I})}} _{2\cos(\Phi _{I}-\Phi _{V})}{\Bigr ]}+{\Bigl [}(\underbrace {e^{i(\Phi _{I}+\Phi _{V})}+e^{-i(\Phi _{V}+\Phi _{V})}} _{2\cos(\Phi _{I}+\Phi _{V})}{\Bigr ]}}$

Graphs of current i, voltage v, and power p for an ac circuit with a phase shift between current and voltage.

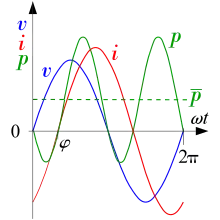
With ac circuits it is customary to average over one period, ${\displaystyle T}$, defined by the expression ${\displaystyle \omega T=2\pi }$.^[1] Using the overbar notation to denote this time average, we have:

${\displaystyle {\overline {IV}}={\tfrac {1}{2}}I_{0}V_{0}\cos(\phi _{i}-\phi _{v})=I_{\text{rms}}V_{\text{rms}}\cos(\phi _{i}-\phi _{v})}$

Footnotes

1. ↑ We may also average over an integral number of periods. Or, with minimal error, we may simply average over any interval of time much greater than T.