Mathematical Definition: Weighted moving average
In technical analysis of financial data, a weighted moving average (WMA) has the specific meaning of weights that decrease in arithmetical progression.[1] In an n-day WMA the latest day has weight n, the second latest n − 1, etc., down to one. These weights create a discrete probability distribution with:
- and
The weighted moving average can be calculated for with the discrete probability mass function at time , where is the initial day, when data collection of the financial data begins and the price/cost of a product at day . the price/cost of a product at day for an arbitrary day x.
The denominator is a triangle number equal to which creates a discrete probability distribution by:
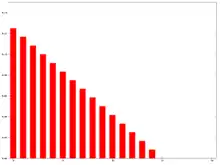
The graph at the right shows how the weights decrease, from highest weight at day t for the most recent datum points, down to zero at day t-n.
In the more general case with weights the denominator will always be the sum of the individual weights, i.e.:
- and as weight for for the most recent datum points at day t and as weight for the day , which is n-th day before the most recent day .
The discrete probability distribution is defined by:
The weighted moving average with arbitrary weights is calculated by:
This general approach can be compared to the weights in the exponential moving average in the following section.
- ↑ "Weighted Moving Averages: The Basics". Investopedia.