Electromagnetic wave radiation

Electromagnetic wave radiation refers to propagation of electromagnetic wave in space at speed of light carries an energy level of a Quanta called Photon

v=\omega ={\sqrt {\frac {1}{\mu \epsilon }}}=C=\lambda f

E=pv=pC=p\lambda f=hf=h{\frac {\omega }{2\pi }}=\hbar \omega

h=p\lambda

p={\frac {h}{\lambda }}=h{\frac {k}{2\pi }}=\hbar k

\lambda ={\frac {h}{p}}

\omega ={\frac {E}{\hbar }}

k={\frac {p}{\hbar }}

\hbar ={\frac {h}{2\pi }}={\frac {E}{\omega }}={\frac {p}{k}}

Characteristics

Quantization

Electromagnetic wave radiation are quantized as a packet of photon's energy

h=p\lambda

Wave-Particle Duality

Quanta ; h ; sometime behaves like a wave of wavelength λ and somtime behave like a particle of a momentum p

Wave like .

\lambda ={\frac {h}{p}}

Particle like .

p={\frac {h}{\lambda }}

Electromagnetic wave radiation states

Electromagnetic wave radiations exist in the form of quantum's energy called photon . Electromagnetic photons are found in 2 states Radiant photon at threshold frequency and Non radiant photon at frequency above threshold frequency .

Radiant photon .

E=hf_{o}.f_{o}={\frac {C}{\lambda _{o}}}

Non-radiant photon .

E=hf.f>f_{o},f>{\frac {C}{\lambda }}

Electromagnetic photon cannot exit in 2 states at the same time . The chance of finding Electromagnetic photons in any state is one half can be expressed mathematically as

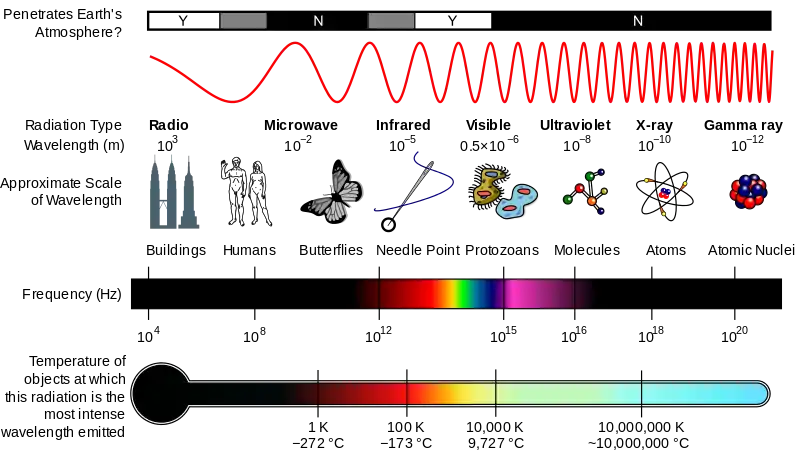
\Delta p\Delta \lambda ={\frac {1}{2}}{\frac {h}{2\pi }}={\frac {h}{4\pi }}={\frac {\hbar }{2}}

Electromagnetic radiation spectrum

The wavefront of electromagnetic waves emitted from a point source (such as a lightbulb) is a sphere. The position of an electromagnetic wave within the electromagnetic spectrum could be characterized by either its frequency of oscillation or its wavelength

Frequency spectrum	$f=f_{o}$	$f>f_{o}$
Speed	$v=C=\lambda _{o}f_{o}$	$v=C=\lambda f$
Work	$E=pv=pC=p\lambda _{o}f_{o}=hf_{o}$	$E=pv=pC=p\lambda f=hf$
Quanta	$h=p\lambda _{o}$	$h=p\lambda$
Momentum	$p={\frac {h}{\lambda _{o}}}$	$p={\frac {h}{\lambda }}$
Wavelength	$\lambda _{o}={\frac {C}{f_{o}}}={\frac {h}{p}}$	$\lambda ={\frac {C}{f}}={\frac {h}{p}}$

The Electromagnetic spectrum includes, in order of increasing frequency and decreasing wavelength

radio waves,
microwaves,
infrared radiation,
visible light,
ultraviolet radiation,
X-rays
gamma rays

Electromagnetic wave radiation and Matter

Heat Transfer

Electromagnetic wave radiation and matter interact creates heat transfer process of 3 phases Heat conduction, Heat convection and Heat radiation

Heat transfer	Heat conduction	Heat convection	Heat radiation
Heat effects	Change matter's temperature $\Delta T=T_{1}-T_{0}$ Matter absorbs heat energy $E=mC\Delta T$	matter absorbs heat energy to its maximum $E=hf_{o}$ at threshold frequency $f_{o}={\frac {C}{\lambda _{o}}}$	matter uses energy above maximum energy to free electron from atom $hf=hf_{o}+{\frac {1}{2}}mv^{2}$ $v={\sqrt {{\frac {2}{m}}(hf-hf_{o})}}={\sqrt {{\frac {2}{m}}(nhf_{o})}}$ With f > fo and hf=(n+1)hfo

Electromagnetic wave radiation types

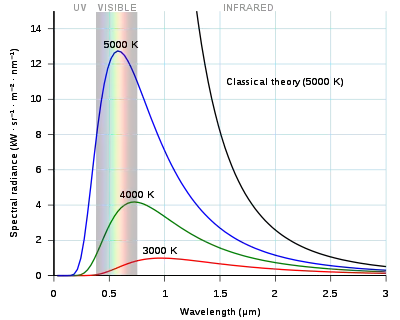
Black Body Radiation

Plank knew that black body absorbs heat better than any other matter . He went go perform an experience on black matter . His experienment has shown that

Planck's law of black-body radiation

Planck's law states that

B_{\nu }(T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{kT}}-1}},

where

B_ν(T) is the spectral radiance (the power per unit solid angle and per unit of area normal to the propagation) density of frequency ν radiation per unit frequency at thermal equilibrium at temperature T.

h is the Planck constant;

c is the speed of light in a vacuum;

k is the Boltzmann constant;

ν is the frequency of the electromagnetic radiation;

T is the absolute temperature of the body.

For a black body surface the spectral radiance density (defined per unit of area normal to the propagation) is independent of the angle $\theta$ of emission with respect to the normal. However, this means that, following Lambert's cosine law, $B_{\nu }(T)\cos \theta$ is the radiance density per unit area of emitting surface as the surface area involved in generating the radiance is increased by a factor $1/\cos \theta$ with respect to an area normal to the propagation direction. At oblique angles, the solid angle spans involved do get smaller, resulting in lower aggregate intensities.

Wien's displacement law

Wien's displacement law shows how the spectrum of black-body radiation at any temperature is related to the spectrum at any other temperature. If we know the shape of the spectrum at one temperature, we can calculate the shape at any other temperature. Spectral intensity can be expressed as a function of wavelength or of frequency.

A consequence of Wien's displacement law is that the wavelength at which the intensity per unit wavelength of the radiation produced by a black body is at a maximum, $\lambda _{\max }$ , is a function only of the temperature:

\lambda _{\max }={\frac {b}{T}},

where the constant b, known as Wien's displacement constant, is equal to 2.8977729(17)×10−3
K m.^[1]

Planck's law was also stated above as a function of frequency. The intensity maximum for this is given by

\nu _{\max }=T\times 58.8\ \mathrm {GHz} /\mathrm {K}

.

Stefan–Boltzmann law

By integrating $B_{\nu }(T)$ over the frequency the integrated radiance $L$ is

L={\frac {2\pi ^{5}}{15}}{\frac {k^{4}T^{4}}{c^{2}h^{3}}}{\frac {1}{\pi }}=:\sigma T^{4}{\frac {1}{\pi }}

by using $\int _{0}^{\infty }dx\,{\frac {x^{3}}{e^{x}-1}}={\frac {\pi ^{4}}{15}}$ with $x\equiv {\frac {h\nu }{kT}}$ and with $\sigma \equiv {\frac {2\pi ^{5}}{15}}{\frac {k^{4}}{c^{2}h^{3}}}=5.670373\times 10^{-8}{\frac {W}{m^{2}K^{4}}}$ being the Stefan–Boltzmann constant. The radiance $L$ is then

\sigma T^{4}{\frac {\cos \theta }{\pi }}

per unit of emitting surface.

On a side note, at a distance d, the intensity $dI$ per area $dA$ of radiating surface is the useful expression

dI=\sigma T^{4}{\frac {\cos \theta }{\pi d^{2}}}dA

when the receiving surface is perpendicular to the radiation.

By subsequently integrating over the solid angle $\Omega$ (where $\theta <\pi /2$ ) the Stefan–Boltzmann law is calculated, stating that the power j* emitted per unit area of the surface of a black body is directly proportional to the fourth power of its absolute temperature:

j^{\star }=\sigma T^{4},

by using

\int \cos \theta \,d\Omega =\int _{0}^{2\pi }\int _{0}^{\pi /2}\cos \theta \sin \theta \,d\theta \,d\phi =\pi .

Sun's Light Decomposition

When visible light interacts with prism, visible light will decompose itself into color lights of six color Red, Orange, Yellow, Violet, Blue and Green

Color	Angle of diffraction	Wavelength
Red
Orange
Yellow
Violet
Blue
Green

Reference

↑ http://physics.nist.gov/cgi-bin/cuu/Value?bwien

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] ttp://physics.nist.gov/cgi-bin/cuu/Value?bwien