NINTH. The compound intervals called ninths exceed the octave either by a tone or a semitone; if the former the ninth is called 'major' (a), if the latter it is called 'minor' (b). The interval of an 'augmented ninth' which exceeds the octave by three semitones (c) also occasionally occurs, as will be presently noted, but it has not by any means the prominence and importance of the major and minor forms. (Ex. 1.)
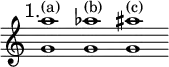
Ninths differ from all other compound intervals in the higher degree of invariability with which they are distinct both in character and treatment from their corresponding simple intervals the major, minor, and augmented seconds. They may be broadly divided into two classes—those which require preparation somewhat peremptorily, and further prompt resolution after percussion; and those which satisfy the understanding ear so far that preparation appears superfluous, and haste to change the harmony after percussion unnecessary. The former belong to the class of artificial combinations arrived at by processes which imply counterpoint, and the latter to that of essential or fundamental chords which can exist intelligibly in the sense of harmony alone.
The first class is generally divided by theorists into two sub-classes, called respectively 'suspensions' and 'prepared discords.' The intimate relationship of these chords has already been indicated in the article Harmony; the above classification will therefore only be accepted here provisionally, for convenience in explanation. Suspended ninths which are resolved while the chord which accompanies them stands still, can occur on every note of the scale, though that on the leading note is extremely harsh; they are commonly accompanied by third and fifth, as in Ex. 2, and not unfrequently by a major seventh, suspended with the ninth, and resolving with it; sometimes also by a suspended fourth as well, which resolves on the third simultaneously with the resolution of the ninth and seventh. Suspended major ninths resolve either upwards or downwards; in the former case alone they resemble suspended seconds, which obviously must rise in resolution; and in this form also the artificial chromatic heightening of the major ninth to an augmented ninth takes place, as in the following, from the Vorspiel to Wagner's Tristan und Isolde. (Ex. 3.)
2. Beethoven.
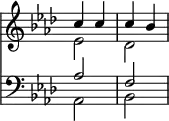
3. Wagner.
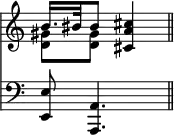
This device is similar to the chromatic alteration of the augmented fifth; and, in fact, eight bars further on than the above quotation, the augmented ninth and the augmented fifth actually occur together in the same chord, in a way which is highly suggestive of their common origin.
The second sub-class mentioned above differs from those which are distinguished as suspensions chiefly in the process of resolution; in which, instead of the rest of the chord (that is, its root and concordant notes) being stationary while the suspended notes are resolved, and moving afterwards, the process is condensed, so that when the discord has been arrived at by preparation, which is practically the same as the process of suspension, the root of the chord and its dependent notes change simultaneously with the resolution. So that though the resolution is upon the same note as it would have been if the chord had remained unchanged, its relation to the root note of the new chord is different. The root commonly rises a fourth, but it is also possible for it to fall a third.
The above class of ninths may be accompanied by thirds and sevenths which are either major or minor, but in the last and most important class the accompanying third must be major and the seventh minor. These ninths, both major and minor, are commonly held to be fundamental harmonies, on the ground of their representing the compound tone of the root or generator. The major ninth is represented by the eighth harmonic, which is only removed two octaves and a note from the root,—and is easily and clearly obtained, as for instance in horns and trumpets. The minor ninth is similarly taken by some theorists to be represented by the sixteenth harmonic, which however is four octaves removed from the generator, and is so closely hemmed in by other harmonics at the distance of a semitone apart, that it seems doubtful if it could be clearly distinguished or easily obtained as the major ninth is. It may however possibly be taken as a modification or softening of the major ninth, and is certainly used with equal freedom. Examples from so trustworthy a source as Haydn, are given in the article Harmony (p. 683): Schumann's Overture to Genoveva actually commences with a full chord of the minor ninth; and Mendelssohn's Andante con Variazioni in E♭, with second inversion of the major ninth.
The ninths belonging to this class are not only free in the manner of their assumption, but singularly so in the manner of their resolution; they are both commonly resolved after the manner of suspensions, either upwards or downwards, while the rest of the chord stands still; or after the manner of the so-called 'prepared' discords; while the chord changes, as from Dominant to Tonic harmony. They also resolve by leaps, as in the case of the Dominant ninths; in which the part having the ninth frequently leaps downwards to the third or fifth of the chord, and then passes with change of harmony to a proximate concordant note in the Tonic chord. Occasionally the ninth appears to be resolved rather by a change of the mass of harmony than by the progression of the parts; and further it is found persisting through such changes of harmony, and being resolved without moving, as in the following from Mr. Macfarren's 'Joseph':—
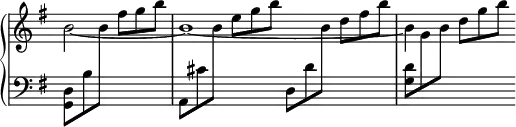
The Dominant major ninth is only used in the major mode, the minor ninth in both; and it will be clear at the mere statement that the minor ninth from the Dominant is not a note which occurs in the diatonic series of the major scale, and therefore the chord is chromatic in that relation. But not only this ninth, but several others which are more distinctly chromatic, are commonly affiliated in the range of a key without its being considered that the tonality is thereby obscured. The most conspicuous of these are the ninths of the Tonic and Supertonic, which represent the compound tone of those respective notes, and also stand in the favourable position of Dominant chords in the closely related keys of the Subdominant and Dominant to the original key. In these the minor seventh and minor ninth of the Tonic, and the major third and minor ninth of the Supertonic are chromatic in relation to the major scale. The major ninth of the Supertonic will not chime conveniently with the minor mode because of its contradicting the vital minor third of the scale; in all the other ninths which can be used in either scale, there will be at least one note which is chromatic.
From the minor ninth are derived that conspicuous class of discords called diminished sevenths, which are its inversions with the root-note omitted. They are said theoretically, that is in just intonation, to be very harsh; but modern musicians seem to be exceedingly well content, with the chord, and even go to the length of using the interval of a diminished seventh melodically; which shows at least that the mind can readily grasp it. This facility may of course be partly owing to the frequency with which the chord occurs in modern music. Theorists have complained that it is used to excess, and in some senses this may be true; but if so it is not unlikely that it is a good deal their fault, for they rarely miss the opportunity to show off much superfluous ingenuity in pointing out to their disciples the chameleonlike qualities of the chord and its various uses, which it would be much better for worthy disciples to find out for themselves. It may comfort those who feel disposed to use the chord a good deal at times for really musical purposes, to point out a singular example in a prelude in G minor for organ, by Bach (Dörffel No. 822), too long for quotation, in which there is a descending series of twelve diminished sevenths alternating with transitional resolutions, and followed by four more diminished sevenths descending in a row; making in all a notable total of sixteen diminished sevenths in thirteen bars.
Further particulars concerning the characteristics of this chord will be found under the heads of Diminished Interval and Change.
The complete chord of the Dominant ninth is sometimes called the 'Added ninth' because the third which produces the interval is added to the complete chord of the Dominant seventh.[ C.H.H.P. ]