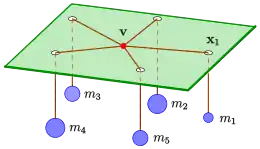
The Varignon frame, named after Pierre Varignon, is a mechanical device which can be used to determine an optimal location of a warehouse for the destribution of goods to a set of shops. Optimal means that the sum of the weighted distances of the shops to the warehouse should be minimal. The frame consists of a board with n holes corresponding to the n shops at the locations , n strings are tied together in a knot at one end, the loose ends are passed, one each, through the holes and are attached to weights below the board (see diagram). If the influence of friction and other odds of the real world are neglected, the knot will take a position of equilibrium . It can be shown (see below), that point is the optimal location which minimizes the weighted sum of distances
- (1): .
The optimization problem is called Weber problem.[1]
Mechanical Problem - Optimization Problem
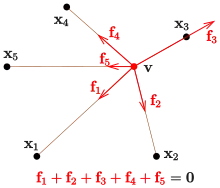
If the holes have locations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): {\displaystyle \mathbf x_1, \dots, \mathbf x_n} and the masses of the weights are then the force acting at the i-th string has the magnitude (: constant of gravity) and direction (unitvector). Summing up all forces and cancelling the common term one gets the equation
- (2):.
(At the point of equilibrium the sum of all forces is zero !)
This is a non-linear system for the coordinates of point which can be solved iteratively by the Weiszfeld-algorithm (see below)[2]
The connection between equation (1) and equation (2) is:
- (3):
Hence Function has at point a local extremum and the Varignon frame provides the optimal location experimentally.
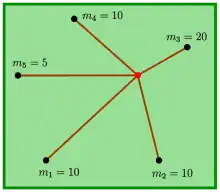
Example
For the following example the points are
and the weights
- .
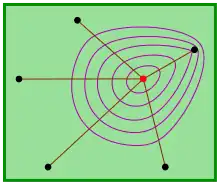
The coordinates of the optimal solution (red) are and the optimal weighted sum of lengths is . The second picture shows level curves which consist of points of equal but not optimal sums. Level curves can be used for assigning areas, where the weighted sums do not exceed a fixed level. Geometrically they are implicit curves with equations
- (see equation (1)).
Special cases n=1 und n=2
- In case of one gets .
- In case of and one gets .
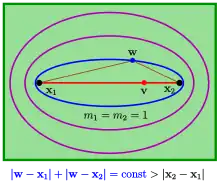
- In case of and point can be any point of the line section (see diagram). In this case the level curves (points with the same not-optimal sum) are confocal ellipses with the points as common foci.
Weiszfeld-algorithm and a fixpoint problem
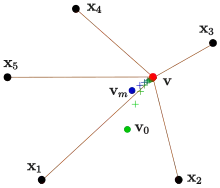
Replacing in formula (2) vector in the nominator by and in the denominator by and solving the equation for one gets:[3]
- (4):
which describes an iteration. A suitable starting point is the center of mass with mass in point :
- .
This algorithm is called Weiszfeld-algorithm.[4]
Formula (4) can be seen as the iteration formula for determining the fixed point of function
- (5)
with fixpoint equation
(see fixed point)
Remark on numerical problems:
The iteration algorithm described here may have numerical problems if point is close to one of the points .
See also
External links
References
- ↑ Z. Drezner, H.W. Hamacher: Facility Location, Springer, 2004, ISBN 3-540-21345-7, p. 7
- ↑ Horst W. Hamacher: Mathematische Lösungsverfahren für planare Standortprobleme, Vieweg+Teubner-Verlag, 2019, ISBN 978-3-663-01968-8, p. 31
- ↑ Karl-Werner Hansmann :Industrielles Management, De Gruyter Verlag, 2014, ISBN 9783486840827, S. 115
- ↑ see Facility location, p. 9
- Uwe Götze: Risikomanagement, Physica-Verlag HD, 2013, ISBN 978-3-642-57587-7, S. 268
- Andrew Wood, Susan Roberts : Economic Geography, Taylor & Francis, 2012, ISBN 9781136899478, p. 22
- H. A. Eiselt, Carl-Louis Sandblom :Operations Research, Springer Berlin Heidelberg, 2010, ISBN 9783642103261, p. 239
- Robert E. Kuenne: General Equilibrium Economics, Palgrave Macmillan UK, 1992, ISBN 9781349127528, p. 226