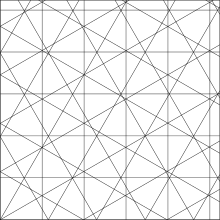
Steinhaus longimeter
The Steinhaus longimeter, patented by the professor Hugo Steinhaus, is an instrument used to measure the lengths of curves on maps.
Description
It is a transparent sheet of three grids, turned against each other by 30 degrees, each consisting of parallel lines spaced at equal distances 3.82 mm. The measurement is done by counting crossings of the curve with grid lines. The number of crossings is the approximate length of the curve in millimetres.
The design of the Steinhaus longimeter can be seen as an application of the Crofton formula, according to which the length of a curve equals the expected number of times it is crossed by a random line.[1]
See also
- Opisometer, a mechanical device for measuring curve length by rolling a small wheel along the curve
- Dot planimeter, a similar transparency-based device for estimating area, based on Pick's theorem
References
- ↑ Maling, D. H. (2016), Measurements from Maps: Principles and Methods of Cartometry, Butterworth-Heinemann, p. 48, ISBN 9780080984124
Bibliography
- Hugo Steinhaus: Zur Praxis der Rectification und zum Längenbegriff, Berichte der Sächsischen Akademie der Wissenschaften 82, 120–130, 1930.
- Hugo Steinhaus: Przeglad Geogr. 21, 1947.
- Hugo Steinhaus: Comptes Rendus Soc. des Sciences et des Lettres de Wrocław, Sér. B, 1949.
- Hugo Steinhaus: Length, shape and area, Colloquium Mathematicum 3(1), 1–13, 1954.
- Hugo Steinhaus: Mathematical Snapshots, 3rd ed. New York: Dover, pp. 105–110, 1999.
External links
- Weisstein, Eric W. "Longimeter." From MathWorld — A Wolfram Web Resource.
- Information about patent (DRGM 1241513)
- Download a PDF recreation of the Longimeter
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.