In the mathematical discipline of graph theory, Shannon multigraphs, named after Claude Shannon by Vizing (1965), are a special type of triangle graphs, which are used in the field of edge coloring in particular.
- A Shannon multigraph is multigraph with 3 vertices for which either of the following conditions holds:
- a) all 3 vertices are connected by the same number of edges.
- b) as in a) and one additional edge is added.
More precisely one speaks of Shannon multigraph Sh(n), if the three vertices are connected by , and edges respectively. This multigraph has maximum degree n. Its multiplicity (the maximum number of edges in a set of edges that all have the same endpoints) is .
Examples
- Shannon multigraphs
 Sh(2)
Sh(2)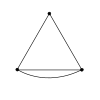 Sh(3)
Sh(3)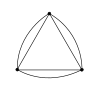 Sh(4)
Sh(4)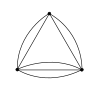 Sh(5)
Sh(5)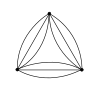 Sh(6)
Sh(6)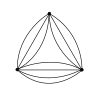 Sh(7)
Sh(7)
Edge coloring

According to a theorem of Shannon (1949), every multigraph with maximum degree has an edge coloring that uses at most colors. When is even, the example of the Shannon multigraph with multiplicity shows that this bound is tight: the vertex degree is exactly , but each of the edges is adjacent to every other edge, so it requires colors in any proper edge coloring.
A version of Vizing's theorem (Vizing 1964) states that every multigraph with maximum degree and multiplicity may be colored using at most colors. Again, this bound is tight for the Shannon multigraphs.
References
- Fiorini, S.; Wilson, Robin James (1977), Edge-colourings of graphs, Research Notes in Mathematics, vol. 16, London: Pitman, p. 34, ISBN 0-273-01129-4, MR 0543798
- Shannon, Claude E. (1949), "A theorem on coloring the lines of a network", J. Math. Physics, 28: 148–151, doi:10.1002/sapm1949281148, hdl:10338.dmlcz/101098, MR 0030203.
- Volkmann, Lutz (1996), Fundamente der Graphentheorie (in German), Wien: Springer, p. 289, ISBN 3-211-82774-9.
- Vizing, V. G. (1964), "On an estimate of the chromatic class of a p-graph", Diskret. Analiz., 3: 25–30, MR 0180505.
- Vizing, V. G. (1965), "The chromatic class of a multigraph", Kibernetika, 1965 (3): 29–39, MR 0189915.
External links
- Lutz Volkmann: Graphen an allen Ecken und Kanten. Lecture notes 2006, p. 242 (German)