Risk aversion is a preference for a sure outcome over a gamble with higher or equal expected value. Conversely, rejection of a sure thing in favor of a gamble of lower or equal expected value is known as risk-seeking behavior.
The psychophysics of chance induce overweighting of sure things and of improbable events, relative to events of moderate probability. Underweighting of moderate and high probabilities relative to sure things contributes to risk aversion in the realm of gains by reducing the attractiveness of positive gambles. The same effect also contributes to risk seeking in losses by attenuating the aversiveness of negative gambles. Low probabilities, however, are overweighted, which reverses the pattern described above: low probabilities enhance the value of long-shots and amplify aversion to a small chance of a severe loss. Consequently, people are often risk seeking in dealing with improbable gains and risk averse in dealing with unlikely losses.[1]
Related theories
Most theoretical analyses of risky choices depict each option as a gamble that can yield various outcomes with different probabilities.[2] Widely accepted risk-aversion theories, including Expected Utility Theory (EUT) and Prospect Theory (PT), arrive at risk aversion only indirectly, as a side effect of how outcomes are valued or how probabilities are judged.[3] In these analyses, a value function indexes the attractiveness of varying outcomes, a weighting function quantifies the impact of probabilities, and value and weight are combined to establish a utility for each course of action.[2] This last step, combining the weight and value in a meaningful way to make a decision, remains sub-optimal in EUT and PT, as people's psychological assessments of risk do not match objective assessments.
Expected utility theory
Expected Utility Theory (EUT) poses a utility calculation linearly combining weights and values of the probabilities associated with various outcomes. By presuming that decision-makers themselves incorporate an accurate weighting of probabilities into calculating expected values for their decision-making, EUT assumes that people's subjective probability-weighting matches objective probability differences, when they are, in reality, exceedingly disparate.[2]
Consider the choice between a prospect that offers an 85% chance to win $1000 (with a 15% chance to win nothing) and the alternative of receiving $800 for sure. A large majority of people prefer the sure thing over the gamble, although the gamble has higher (mathematical) expected value (also known as expectation). The expected value of a monetary gamble is a weighted average, in which each possible outcome is weighted by its probability of occurrence. The expected value of the gamble in this example is .85 X $1000 + .15 X $0 = $850, which exceeds the expected value of $800 associated with the sure thing. [1]
Research suggests that people do not evaluate prospects by the expected value of their monetary outcomes, but rather by the expected value of the subjective value of these outcomes (see also Expected utility).[4] In most real-life situations, the probabilities associated with each outcome are not specified by the situation, but have to be subjectively estimated by the decision-maker.[5] The subjective value of a gamble is again a weighted average, but now it is the subjective value of each outcome that is weighted by its probability.[1] To explain risk aversion within this framework, Bernoulli proposed that subjective value, or utility, is a concave function of money. In such a function, the difference between the utilities of $200 and $100, for example, is greater than the utility difference between $1,200 and $1,100. It follows from concavity that the subjective value attached to a gain of $800 is more than 80% of the value of a gain of $1,000.[1] Consequently, the concavity of the utility function entails a risk averse preference for a sure gain of $800 over an 80% chance to win $1,000, although the two prospects have the same monetary expected value.[1]
While EUT has dominated the analysis of decision-making under risk and has generally been accepted as a normative model of rational choice (telling us how we should make decisions), descriptive models of how people actually behave deviate significantly from this normative model.[5]
Modern Portfolio Theory
Modern Portfolio Theory (MPT) was created by economist Harry Markowitz in 1952 to mathematically measure an individual's risk tolerance and reward expectations.[6] The theory was that constant variance allowed for a maximized expected return and to gain a constant expected return variance should be minimized. An asset must be considered in regard to how they will move within the market and by taking these movements into account an investment portfolio can be constructed that decreased risk and had a constant expected return.[6]
The levels of additional expected returns are calculated as the standard deviation of the return on investment (square root of the variance).[6] Standard deviation illustrates the fluctuation of an asset's returns over the period of time creating an accepted trading range to estimate possible returns on the asset.[6] This tool enables individuals to determine their level of risk aversion to create a diversified portfolio.
MPT has been critiqued for using standard deviation as a form of measurement.[7] Standard deviation is a relative form of measurement and investors using this index for their risk assessment must analyse an appropriate context in which the market sits to ensure a quantified understanding of what the standard deviation means.[7] MPT automatically assumes that investors have an aversion towards risk however can be used by all types of investors to suit their needs individually. Furthermore, under MPT, two portfolios could be represented by the same level of variance hence would be considered equally desirable. The first portfolio may experience small losses frequently, and the second may experience a singular decline. This contrast between portfolios needs to be examined by investors prior to their purchasing of assets. By eliminating downside risk instead of volatility, Post-modern portfolio theory aims to build on MPT.[7]
Prospect theory and gain-loss asymmetry (S-shaped value function)
Prospect Theory (PT) claims that fair gambles (gambles in which the expected value of the current option and all other alternatives are held equal) are unattractive on the gain side but attractive on the loss side. In contrast to EUT, PT is posited as an alternative theory of choice, in which value is assigned to gains and losses rather than to final assets (total wealth), and in which probabilities are replaced by decision weights.[8] In an effort to capture inconsistencies in our preferences, PT offers a non-linear, S-shaped probability-weighted value function, implying that the decision-maker transforms probabilities along a diminishing sensitivity curve, in which the impact of a given change in probability diminishes with its distance from impossibility and certainty.[1]
The value function shown is:
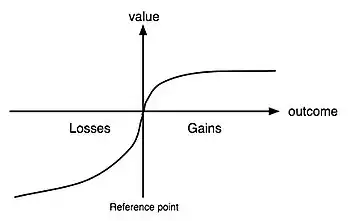
A. Defined on gains and losses rather than on total wealth.[1] Prospects are coded as gains and losses from a zero point (e.g. using current wealth, rather than total wealth as a reference point), leading people to be risk averse for gains and risk seeking for losses.[5]
B. Concave in the domain of gains (risk aversion) and convex in the domain of losses (risk seeking).[1] The negatively accelerated nature of the function implies that people are risk averse for gains and risk seeking for losses.[5]
C. Considerably steeper for losses than for gains (see also loss aversion).[1] Steepness of the utility function in the negative direction (for losses over gains) explains why people are risk-averse even for gambles with positive expected values.[5]
While risk aversion is not part of PT per se, a pertinent part of PT is gain-loss asymmetry with regard to risk. PT's S-shaped probability-weighted, non-linear value function deems risk aversion context-dependent, as the gain-loss asymmetry illustrated above, results from our psychological assessments of risk hardly matching objective assessments of risk. One conceivable component of risk aversion in the framework of PT is that the degree of risk aversion apparent will vary depending on where along the curve our decision lies.
Example: Participants are indifferent between receiving a lottery ticket offering a 1% chance at $200 and receiving $10 for sure. Additionally, people are indifferent between receiving a lottery ticket offering a 99% chance at $200 and receiving $188 for sure. [9]
In line with diminishing sensitivity, the first hundredth of probability is worth $10, and the last hundredth is worth $12, but the 98 intermediate hundredths are worth only $178, or about $1.80 per hundredth. PT captures this pattern of differentially weighting (objective) probabilities subjectively with an S-shaped weighting function.[9]
Framing effects
A framing effect occurs when transparently and objectively identical situations generate dramatically different decisions depending on whether the situations are presented or perceived as either potential losses or gains.[10] Framing effects play an integral role in risk-aversion, as an extension of PT's S-shaped value function, which illustrates the differences in how gains and losses are valued relative to a reference point.
Risky prospects are characterized by their possible outcomes and by the probabilities of these outcomes.[10] The same, possible outcomes of a gamble can be framed either as gains or as losses relative to the status quo. The following pair of problems attests to the power of framing effects in manipulating either risk-averse or risk-seeking behavior.
The total number of respondents in each problem is denoted by N, and the percentage who chose each option is indicated in parentheses.
Problem 1 (N = 152): Imagine that the U.S. is preparing for the outbreak of an unusual disease, which is expected to kill 600 people. Two alternative programs to combat the disease have been proposed. Assume that the exact scientific estimates of the consequences of the programs are as follows:
If Program A is adopted, 200 people will be saved. (72%)
If Program B is adopted, there is a one-third probability that 600 people will be saved and a two-thirds probability that no people will be saved. (28%)
Which of the two programs would you favor?.[1]
The formulation of Problem 1 implicitly adopts as a reference point a state of affairs in which the disease is allowed to take its toll of 600 lives. The outcomes of the programs include the reference state and two possible gains, measured by the number of lives saved. As expected, preferences are risk averse: a clear majority of respondents prefer saving 200 lives for sure over a gamble that offers a one-third chance of saving 600 lives.
Now consider another problem in which the same cover story is followed by a different description of the prospects associated with the two programs:
Problem 2 (N = 155): Imagine that the U.S. is preparing for the outbreak of an unusual disease, which is expected to kill 600 people. Two alternative programs to combat the disease have been proposed. Assume that the exact scientific estimates of the consequences of the programs are as follows:
If Program C is adopted, 400 people will die. (22%)
If Program D is adopted, there is a one-third probability that nobody will die and a two-thirds probability that 600 people will die. (78%)
It is easy to verify that options C and D in Problem 2 are indistinguishable in real terms from options A and B in Problem 1, respectively. The second version, however, assumes a reference state in which no one dies of the disease. The best outcome is the maintenance of this state and the alternatives are losses measured by the number of people that will die of the disease. People who evaluate options in these terms are expected to show a risk-seeking preference for the gamble (option D) over the sure loss of 400 lives. Of course, the "sure loss" of 400 lives that participants found so unattractive is exactly the same outcome as the "sure gain" of 200 subjects found so attractive in the Problem 1.[5] The public health problem illustrates a formulation effect in which a change of wording from "lives saved" to "lives lost" induced a marked shift of preference from risk aversion to risk seeking.[1]
If preferences reverse based on inconsequential aspects of how the problem is framed, people cannot possibly be maximizing expected utility.[5] Latent here is the unsettling idea that people's preferences come from the outside (from whoever has the power to shape the environment and determine how questions are phrased), rather than from their own psychological makeup.[5] Decision-making in matters as important as lives saved or lives lost can reverse risk preference. This may be based on a rephrasing of the outcomes that conveys no differential information about the treatments and that changes nothing about the outcomes themselves.[5]
Phenomena
While risk aversion is commonly explained through EUT and PT, observed risk-aversion behavior remains solely an artifact of these two theories, and extends beyond the bounds of what each theory can explain.
Direct risk aversion
Both EUT and PT make the following falsifiable prediction: an individual cannot be so risk averse as to value a risky prospect less than the prospect's worst possible outcome.[3] On the contrary, several between-participant studies have found that people are willing to pay less, on average, for a binary lottery than for its worse outcome, a finding coined the uncertainty effect (UE).[11]
For example, people are willing to pay an average of $26 for a $50 gift certificate, but only $16 for a lottery that pays either a $50 or $100 gift certificate, with equal probability. [11]
UE, valuing a risky prospect below the value of its worse possible outcome, occurs as the result of a phenomenon known as direct risk aversion, a literal distaste for uncertainty, as uncertainty itself enters directly into people's utility function.[3]
Societal applications
EUT and PT predict that people should not purchase insurance for small-stakes risks, yet such forms of insurance (e.g., electronic warranties, insurance policies with low deductibles, mail insurance, etc.) are very popular.[3] Direct risk aversion may explain why, as people demonstrate their literal distaste for any and all levels of uncertainty. By paying a premium (often higher than the cost of replacement) for the possibility that insurance may come in handy, people display direct risk aversion by valuing a risky prospect below the value of its worst possible outcome (replacement at face-value).
Suppose you are undecided whether or not to purchase earthquake insurance because the premium is quite high. As you hesitate, your friendly insurance agent comes forth with an alternative offer: "For half the regular premium you can be fully covered if the quake occurs on an odd day of the month. This is a good deal because for half the price you are covered for more than half the days."
Why do most people find such probabilistic insurance distinctly unattractive? Starting anywhere in the region of low probabilities, the impact on the decision weight of a reduction of probability from p to p/2 is considerably smaller than the effect of a reduction from p/2 to 0. Reducing the risk by half, then, is not worth half the premium.
The aversion to probabilistic insurance is significant for three reasons. First, it undermines the classical explanation of insurance in terms of a concave utility function.[1] According to EUT, probabilistic insurance should be definitely preferred to normal insurance when the latter is just acceptable.[8] Second, probabilistic insurance represents many forms of protective action, such as having a medical checkup, buying new tires, or installing a burglar alarm system.[1] Such actions typically reduce the probability of some hazard without eliminating it altogether.[1] Third, the acceptability of insurance can be manipulated by the framing of the contingencies.[1] An insurance policy that covers fire but not flood, for example, could be evaluated either as full protection against a specific risk, (e.g., fire) or as a reduction in the overall probability of property loss.[1] People greatly undervalue a reduction in the probability of a hazard in comparison to the complete elimination of that hazard.[1] Hence, insurance should appear more attractive when it is framed as the elimination of risk than when it is described as a reduction of risk.[1]
Further, Slovic, Fischhoff, and Lichtenstein (1982)[12] showed that a hypothetical vaccine that reduces the probability of contracting a disease from 20% to 10% is less attractive if it is described as effective in half of the cases than if it is presented as fully effective against one of two exclusive and equally probable virus strains that produce identical symptoms.[13]
Affective psychology of risk
The earliest studies of risk perception also found that, whereas risk and benefit tend to be positively correlated in the world, they are negatively correlated in people's minds, and, therefore, judgments.[14] The significance of this finding was not realized until a study by Alhakami and Slovic (1994) found that the inverse relation between perceived risk and perceived benefit of an activity (e.g., using pesticides) was linked to the strength of positive or negative affect associated with that activity as measured by rating the activity on bipolar scales such as good/bad, nice/awful, dread/not dread, and so forth.[15] This result implies that people base their judgments of an activity or a technology not only on what they think about it but also on how they feel about it.[13] If their feelings toward an activity are favorable, they are moved toward judging the risks as low and the benefits as high; if their feelings toward it are unfavorable, they tend to judge the opposite— high risk and low benefit (see also affect heuristic).[13]
Both EUT and PT are probability-outcome independent theories, as they posit separate functions for the evaluation of outcomes and probabilities.[2] Both assume that the impact of a given probability is a function of that probability but not of the outcome to which it's attached.[2] Further, neither theory distinguishes one source of value from another.[2] While probability-outcome independence may hold across outcomes of different monetary values, it is unlikely to hold across outcomes of varying affects.[2]
Realm of gains
In 2001, two researchers from the University of Chicago, Rottenstreich and Hsee, conducted a series of three experiments to illustrate probability-outcome dependence, using an affective approach.[2]
Experiment 1: In an experiment observing probability-outcome interactions, a lottery ticket offers you a chance to meet and kiss your favorite movie-star as a prize (affect-rich) or $50 in cash (affect-poor). Each of the two conditions poses a 1% probability of the respective gamble occurring.
Results & Implications: 70% of participants preferred the cash to the kiss under certainty, whereas 65% (nearly the reverse) preferred the kiss to the cash under low probability. This indicates that we weight what should be an objectively equal 1% probability in each scenario differently: a 1% probability is greater for the affect-rich kiss than for the affect-poor cash.
Experiment 2: In a subsequent, and more realistic study, two similar and financially equivalent prizes - a $500 coupon redeemable toward payments associated with a European vacation (affect-rich) and a $500 coupon redeemable toward payment of tuition (affect-poor) were presented. For each prize, some participants were told they had a 1% chance of winning, and others a 99% chance of winning. Participants then had to indicate how much money they would have to be offered for them to be indifferent between receiving that dollar amount for sure and having the specified chance of winning the prize.
Results & Implications: Although the two coupons had equivalent redemption values, the median price of the 1% chance of winning the European vacation was $20, but $5 for the tuition coupon, indicating that the weight of 1% we place on affect-rich prizes is greater than for affect-poor prizes. Based on results from the 1% condition, PT would predict that at a 99% chance of winning, the European coupon would still be priced higher than the tuition coupon. On the contrary, the affective approach found that in the 99% chance of winning condition, the median price of the European coupon was $450, whereas that of the tuition coupon was $478. Our weighting of the 99% probability as smaller for the affect-rich European coupon than the affect-poor tuition coupon indicates probability-outcome dependence for affect-rich outcomes. Affect-rich outcomes yield more pronounced overweighting of small probabilities, but more pronounced underweighting of large probabilities.
Both examples indicate probability-outcome dependence, as based on affect-rich outcomes, which changes the shape of PT's S-shaped curve.
In Experiment 2, the size of the affect-rich jump in the weighting function is much greater ($500 – $450 = $50) than the size of the affect-poor jump ($500 – $478 = $22).[2] Thus, weighting functions will be more S-shaped for lotteries involving affect-rich than affect-poor outcomes.[2] That is, people will be more sensitive to departures from impossibility and certainty (from hope and fear), but less sensitive to intermediate probability variations for affect-rich outcomes, resulting in larger jumps at the endpoints of the weighting function.[2] Results from this study suggest that the assumption of probability-outcome independence adopted by both EUT and PT may hold across outcomes of different monetary values, but not different affective values.[2]
Realm of losses
The outcomes studies in Experiments 1 and 2 were gains above the status quo. When a positive outcome is available, any departure from impossibility may engender hope (affect-rich and positive), and any deviation from certainty may produce fear (affect-rich but negative). The following study demonstrates that the opposite pattern is also true: when the available outcome is negative, departures from impossibility engender fear, and deviations from certainty produce hope.
Experiment 3: Participants were told to imagine themselves in a hypothetical experiment entailing either a certain, 1% or 99% chance of a short, painful but not dangerous electric shock (affect-rich), and others were told that the experiment entailed either a 1% or 99% chance of a cash penalty (affect-poor, relatively). They were then asked to indicate how much money they would have to pay for them to be indifferent between paying that amount for sure and participating in the hypothetical experiment.
Certainty condition: The median price paid to avoid an electric shock was $19.86. Most participants (24/30) preferred receiving the shock over paying more than $20.
Low-probability condition: The median price paid to avoid a 1% chance of a shock was $7, substantially greater than the median price paid to avoid a 1% chance of a $20 penalty. As before, the weight of a 1% probability is greater for the affect-rich shock than for the affect-poor cash payment.
High-probability condition: The median price paid to avoid a 99% chance of shock, $10, was substantially lower than the median price paid to avoid a 99% chance of cash penalty, $18.
Results: Taken together, for the affect-rich electric shock, the size of the right-hand jump in the weighting function is about $10 ($19.86 - $10), but for the affect-poor cash penalty, the size of this jump is much smaller at $2 ($20 - $18). Again, we see that the weight of the 99% is smaller for the affect-rich shock than for the affect-poor cash.
Both Experiments 1 and 2 investigated outcomes that were gains over the status quo. Experiment 3 studied negative outcomes and also found evidence of a weighting function that is more S-shaped for affect-rich than affect-poor prizes. Therefore, probability-outcome dependence based on the affect-rich psychology of risk applies in the domains of both gains and losses.[2]
Neuropsychology of risk aversion
Negativity bias
Do you remember the worst thing that has happened to you? What about the best? At what frequency are you able to recall memories that are negative in comparison to those that are positive? Does it seem like negative information is remembered with more ease and clarity than positive information? Why is it easier to know the percentage of fatal car accidents each year, as opposed to the percentage of accidents without fatalities?
The human brain demonstrates a partiality for the processing of negative information. In comparison with their positive counterparts, negative stimuli receive a larger allocation of attention and a swifter response once recognized by the brain.[16][17] This bias for negative information occurs very early on in the stages of processing, seen in the appearance of a P1, a component of the event-related potentials (ERP) gathered from an EEG (electroencephalography) output. Researchers localized this particular ERP to the ventrolateral occipital cortex. Given that a greater amount of attention is allotted to the processing of negative stimuli, the negativity bias may also be indicative of an attentional bias.
The negativity bias is noticeable in a plethora of situations related to the formation of risk-averse behaviour. Notably, any stimuli that evokes the expression of fear encourages risk -aversion. The human brain has adapted to easily parse out these stimuli from a sea of benign stimuli. In the laboratory, participants report and respond more quickly to negative stimuli; Photos of negative and threatening pictures jump out of an array of photos, capturing participants' attention more than positive or neutral pictures.[18] Non-tangibles, such as personality traits, also demonstrate a similar impact for eliciting risk-averse behaviour. Carleston & Skowronski (1989) found that negative traits form a stronger impression on an individual than positive traits, thus affecting the overall impression of the individual being evaluated.[19]
Emotion and decision making
An individual's affect often determines the extent to which one's behaviour is effective in obtaining their goal. Decision making and emotion, intertwined, cannot be separated from each other, as emotion can either benefit or hinder the attainment of maximized utility.
Influence of emotion on decision making
Three different emotional states influence decision making: Your current emotional state (i.e. How do you feel while you are making a decision?) Your past emotional state (i.e. How did you feel anticipating your decision?) Your future emotional state (i.e. How will your decision affect how you feel in the future; What effect will the decision have on your emotional well-being?)
Iowa gambling task
Researching decision-making and affect, Antoine Bechara, Antonio Damasio and colleagues (2000; 2005) discovered that damage to a brain area associated with emotional processing impairs effective decision-making.[20][21] After discovering that damage to the orbitofrontal cortex impaired participants from making goal-oriented decisions in social and professional contexts, Damasio and his colleagues designed the Iowa Gambling Task. In creating this task, Damasio wondered whether decision-making was afflicted because emotion was a necessary component to making effective decisions.
In the task, participants continuously draw from one out of four possible decks – participants may switch decks at any point during the study.
Each card possesses monetary value, resulting in either gains or losses.
Participants are unaware that 2 of the decks correspond to net winnings – low payoffs and even lower losses. The other 2 decks correspond to net losses – high payoffs and even higher losses.
Researchers instruct participants to maximize their utility – gain the most money by the end of the task. In order to complete this task successfully, participants must discern that the decks associated with net winning, yet low payoffs, maximize their utility.
Results. Damasio noticed that participants with damage to their orbitofrontal cortex were unable to realize that the deck associated with low payoffs yielded higher reward. From his discovery using the Iowa Gambling Task, Damasio formulated a Somatic marker hypothesis.
Alternate Conclusions. Other researchers suggest that the difficulty encountered by patients with orbitofrontal cortex damage on Iowa Gambling Task is because the task requires participants to change their initial perception of potential gains and losses.[22] Participants are lured in by appealing rewards, then confronted with devastating losses. Thus, orbitofrontal cortex damage inhibits the adaptation to changing patterns of rewards and punishment. This conclusion has been replicated in primates, where orbitofrontal damage prevented the extinction of a learned association.[23]
Somatic marker theory
Damasio posited that emotional information in the form of physiological arousal, is needed to inform decision making. When confronted with a decision, we may react emotionally to the situation, a reaction that manifests as changes in physiological arousal in the body, or somatic markers. Given data collected from the Iowa Gambling Task, Damasio postulated that the orbitofrontal cortex assists individuals in forming an association between somatic markers and the situations that trigger them. Once an association is made, the orbitofrontal cortex and other brain areas evaluate an individual's previous experiences eliciting similar somatic markers. Once recognized, the orbitofrontal cortex can determine an adequate and swift behavioural response, and its likeliness for reward.
Neuroscience of risk aversion
Regret and risk aversion
Several brain areas are observed in the expression of risk-averse behaviour. The previously mentioned orbitofrontal cortex is amongst these brain areas, supporting the feeling of regret. Regret, an emotion which heavily influences decision making, leads individuals to make decisions which circumvent encountering this emotion in the future.
Studying brain activity associated with regret, researcher Georgio Coricelli and his colleagues (2005) triggered feelings of regret in healthy participants, by having them complete a gambling task in which they were informed that the best choice was the unchosen option.[24] Using functional magnetic resonance imaging (fMRI), Coricelli found that increasing regret correlated with increased activity in the medial orbitofrontal cortex, the anterior cingulate cortex, and the anterior hippocampus.[24] The higher the activation in the medial orbitofrontal cortex, the greater the reported regret. After repeated trials, researchers began to observe risk averse behaviour by their participants, a behaviour echoed in intensified activity within the medial orbitofrontal cortex and the amygdala.
Brain areas of risk aversion
Risk-averse behaviors are the culmination of several neural correlates. While avoiding negative stimuli, perceived or real, is a simple enough action, it requires anticipation, motivation and reasoning. How do you know a stimulus is malevolent? What information leads you to ultimately behave in a manner consistent with ensuring or endangering your well-being? Each of these questions recruit a different brain area, playing a poignant role in whether a decision is beneficial to an individual.
Fear-Conditioning. Over time, individuals learn that a stimulus is not benign through personal experience. Implicitly, a fear of a particular stimulus can develop, resulting in risk-averse behaviour. Traditionally, fear-conditioning is not associated with decision-making, but rather the pairing of a neutral stimulus with an aversive situation. Once an association is formed between the neutral stimulus and aversive event, a startle response is observed each time the neutral stimulus is presented. An aversion to the presentation of the neutral stimulus is observed after repeated trials.
Essential to understanding risk aversion is the implicit learning that occurs during fear-conditioning. Risk aversion is the culmination of implicitly or explicitly acquired knowledge that informs an individual that a particular situation is aversive to their psychological well-being. Similarly, fear-conditioning is the acquisition of knowledge that informs an individual that a particular neutral stimulus now predicts an event that endangers their psychological or physical well-being.
Researchers such as Mike Davis (1992) and Joseph LeDoux (1996), have deciphered the neural correlates responsible for the acquisition of fear-conditioning.[25][26]
The amygdala, previously mentioned as a region showing high activity for the emotion of regret, is the central recipient for brain activity concerning fear-conditioning. Several streams of information from multiple brain areas converge on the lateral amygdala, allowing for the creation of associations that regulate fear-conditioning; Cells in the superior dorsal lateral amygdala are able to rapidly pair the neutral stimulus with the aversive stimulus. Cells that project from the lateral amygdala to the central amygdala allow for the initiation of an emotional response if a stimulus is deemed threatening.
Cognitive Control. Evaluating a gamble and calculating its expected value requires a certain amount of cognitive control. Several brain areas are dedicated to monitoring the congruence between expected and actual outcomes. Evidence by Ridderinkhof et al. (2004) suggests that the posterior medial frontal cortex (pMFC) and the lateral prefrontal cortex (LPFC) are involved in goal-directed performance monitoring and behaviour modulation.[27] The pMPC monitors response conflicts (any situation that activates more than one response tendency), decision uncertainty, and any deviation from the anticipated outcome. Activation in the pMPC increases significantly after an error, response conflict, or unfavorable outcome is detected. As a result, the pMFC can signal a need for performance adjustment; there is a lack of evidence, however, indicating that the pMFC controls modulatory behaviour. Behaviour control processes in the LPFC have been implicated in the modulatory behaviour observed by researchers.
Summary
The field of neuroeconomics is emerging as a unified branch of knowledge, intending to merge information from psychology, economics and neuroscience with hopes of better understanding human behaviour. Risk aversion poses a mystifying question that intrigues experts in all three disciplines. Why is it that humans do not act in accord with their anticipated outcome? Whilst negative outcomes retain more value than positive outcome, human beings do not make logical decisions. Parsing out emotion and fear of loss from decision making would result in more implementation of mathematical calculations, thus maximizing expected utility. While activation in specific brain areas can highlight the mechanisms of decision making, evidence continues to support the prevalence of risk-averse behaviour.
See also
References
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Kahneman, D., & Tverksy, A. (1984). "Choices, values, and frames". American Psychologist. 39 (4): 341–350. doi:10.1037/0003-066X.39.4.341.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - 1 2 3 4 5 6 7 8 9 10 11 12 13 Rottenstreich, Y., & Hsee, C.K. (2001). "Money, Kisses, and Electric Shocks: On the Affective Psychology of Risk". Psychological Science. 12 (3): 185–190. doi:10.1111/1467-9280.00334. PMID 11437299. S2CID 16105642.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - 1 2 3 4 Simonsohn, U. (2009). "Direct Risk Aversion: Evidence From Risky Prospects Valued Below Their Worst Outcome" (PDF). Psychological Science. 20 (6): 686–692. doi:10.1111/j.1467-9280.2009.02349.x. PMID 19422629. S2CID 12983766.
- ↑ Bernoulli, D. (1954). "Exposition of a new theory on the measurement of risk". Econometrica. 22 (1): 23–36. doi:10.2307/1909829. JSTOR 1909829.
- 1 2 3 4 5 6 7 8 9 Stanovich, K. E. (2010). Decision Making and Rationality in the Modern World. New York: Oxford. ISBN 978-0-19-532812-7.
- 1 2 3 4 Elton, E. & Gruber, M. (1996). "Modern Portfolio Theory". Journal of Banking and Finance. 21: 1743–1759. doi:10.1016/S0378-4266(97)00048-4. S2CID 2638411.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - 1 2 3 Rom, B. & Ferguson K. (1993). "Post-Modern Portfolio Theory Comes of Age". Journal of Investing. 2 (4): 27–33. doi:10.3905/joi.2.4.27. S2CID 219223515.
- 1 2 Kahneman, D., & Tverksy, A. (1979). "Prospect Theory: An analysis of decision under risk". Econometrica. 47 (2): 263–291. CiteSeerX 10.1.1.407.1910. doi:10.2307/1914185. JSTOR 1914185.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - 1 2 Tversky, A., & Kahneman, D. (1992). "Advances in prospect theory: Cumulative representations of uncertainty". Journal of Risk and Uncertainty. 5 (4): 297–323. CiteSeerX 10.1.1.320.8769. doi:10.1007/bf00122574. S2CID 8456150.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - 1 2 Tversky, A., & Kahneman, D. (1981). "The framing of decisions and the psychology of choice". Science. 211 (4481): 453–458. Bibcode:1981Sci...211..453T. doi:10.1126/science.7455683. PMID 7455683. S2CID 5643902.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - 1 2 Gneezy, U., List, J.A., Wu, G. (2006). "The uncertainty effect: When a risky prospect is valued less than its worse outcome" (PDF). Quarterly Journal of Economics. 121 (4): 1283–1309. doi:10.1093/qje/121.4.1283.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Slovic, P.; Fischhoff, B.; Lichtenstein, S. (1982). "Response mode, framing, and information-processing effects in risk assessment". In Hogarth, R. (ed.). New directions for methodology of social and behavioral science: Question framing and response consistency. San Francisco: Jossey-Bass. pp. 21–36.
- 1 2 3 Slovic, P., & Peters, E., & Finucane, M.L., & MacGregor, D.G. (2005). "Affect, Risk, and Decision Making". Health Psychology. 24 (4, Suppl): S35–S40. CiteSeerX 10.1.1.335.734. doi:10.1037/0278-6133.24.4.s35. hdl:1794/22607. PMID 16045417.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Fischhoff, B., Slovic, P., Lichtenstein, S., Read, S., & Combs, B. (1978). "How safe is safe enough? A Psychometric study of attitudes toward technological risks and benefits". Policy Sciences. 9 (2): 127–152. doi:10.1007/bf00143739. S2CID 154775568.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Alhakami, A.S., & Slovic, P. (1994). "A psychological study of the inverse relationship between perceived risk and perceived benefit". Risk Analysis. 14 (6): 1085–1096. doi:10.1111/j.1539-6924.1994.tb00080.x. hdl:1794/22415. PMID 7846317.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Smith, N., & Larsen, J., & Chartrand, T. (2003). "May I have your attention, please: Electrocortical responses to positive and negative stimuli". Neuropsychologia. 41 (2): 171–183. CiteSeerX 10.1.1.322.5967. doi:10.1016/s0028-3932(02)00147-1. PMID 12459215. S2CID 17367718.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Ito, T. A., Larsen, J. T., Smith, N. K., & Cacioppo, J. T. (1988). "Negative information weighs more heavily on the brain: The negativity bias in evaluative categorizations". Journal of Personality and Social Psychology. 75 (4): 887–900. CiteSeerX 10.1.1.316.2348. doi:10.1037/0022-3514.75.4.887. PMID 9825526.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Öhman, A.; Flykt, A.; Lundqvist, D. (2000). "Unconscious emotion: Evolutionary perspectives, psychophysiological data and neuropsychological mechanisms". In Lane, R. D.; Nadel, L. (eds.). Cognitive Neuroscience of Emotion. Oxford University Press. p. 296. ISBN 978-0-19-515592-1.
- ↑ Skowronski, J. J., & Carlston, D. E. (1989). "Negativity and extremity biases in impression formation: A review of explanations". Psychological Bulletin. 105 (1): 131–142. doi:10.1037/0033-2909.105.1.131.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Bechara, A., Damasio, H., & Damasio, A. R. (2000). "Emotion, decision making and the orbitofrontal cortex". Cerebral Cortex. 10 (3): 295–307. doi:10.1093/cercor/10.3.295. PMID 10731224.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Bechara, A., Damasio, H., Tranel, D., & Damasio, A. R. (2005). "The Iowa Gambling Task and the somatic marker hypothesis: some questions and answers". Trends in Cognitive Sciences. 9 (4): 159–162. doi:10.1016/j.tics.2005.02.002. PMID 15808493. S2CID 2787434.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Fellows, L. K., & Farah, M. J (2005). "Dissociable elements of human foresight: a role for the ventromedial frontal lobes in framing the future, but not in discounting future rewards". Neuropsychologia. 43 (8): 1214–1221. doi:10.1016/j.neuropsychologia.2004.07.018. PMID 15817179. S2CID 14877046.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Jones, B., & Mishkin, M. (1972). "Limbic lesions and the problem of stimulus—reinforcement associations". Experimental Neurology. 36 (2): 362–377. doi:10.1016/0014-4886(72)90030-1. PMID 4626489.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - 1 2 Coricelli, G., Critchley, H. D., Joffily, M., O'Doherty, J. P., Sirigu, A., & Dolan, R. J. (2005). "Regret and its avoidance: a neuroimaging study of choice behavior". Nature Neuroscience. 8 (9): 1255–1262. doi:10.1038/nn1514. hdl:21.11116/0000-0001-A327-B. PMID 16116457. S2CID 9893530.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ LeDoux, J. (1996). "Chapter 26 Emotional networks and motor control: A fearful view". The Emotional Motor System. Progress in Brain Research. Vol. 107. pp. 437–446. doi:10.1016/s0079-6123(08)61880-4. ISBN 978-0-444-81962-8. PMID 8782535.
- ↑ Davis, M. (1992). "The role of the amygdala in fear and anxiety". Annual Review of Neuroscience. 15 (1): 353–375. doi:10.1146/annurev.neuro.15.1.353. PMID 1575447.
- ↑ Ridderinkhof, K. R., Ullsperger, M., Crone, E. A., & Nieuwenhuis, S. (2004). "The role of the medial frontal cortex in cognitive control" (PDF). Science. 306 (5695): 443–447. Bibcode:2004Sci...306..443R. doi:10.1126/science.1100301. hdl:1871/17182. PMID 15486290. S2CID 5692427.
{{cite journal}}: CS1 maint: multiple names: authors list (link)