In mathematics, in the area of algebraic topology, the homotopy extension property indicates which homotopies defined on a subspace can be extended to a homotopy defined on a larger space. The homotopy extension property of cofibrations is dual to the homotopy lifting property that is used to define fibrations.

Definition

Let ${\displaystyle X\,\!}$ be a topological space, and let ${\displaystyle A\subset X}$. We say that the pair ${\displaystyle (X,A)\,\!}$ has the homotopy extension property if, given a homotopy ${\displaystyle f_{\bullet }\colon A\rightarrow Y^{I}}$ and a map ${\displaystyle {\tilde {f}}_{0}\colon X\rightarrow Y}$ such that

$${\displaystyle {\tilde {f}}_{0}\circ \iota =\left.{\tilde {f}}_{0}\right|_{A}=f_{0}=\pi _{0}\circ f_{\bullet },}$$

then there exists an extension of ${\displaystyle f_{\bullet }}$ to a homotopy ${\displaystyle {\tilde {f}}_{\bullet }\colon X\rightarrow Y^{I}}$ such that ${\displaystyle {\tilde {f}}_{\bullet }\circ \iota =\left.{\tilde {f}}_{\bullet }\right|_{A}=f_{\bullet }}$.^[1]

That is, the pair ${\displaystyle (X,A)\,\!}$ has the homotopy extension property if any map ${\displaystyle G\colon ((X\times \{0\})\cup (A\times I))\rightarrow Y}$ can be extended to a map ${\displaystyle G'\colon X\times I\rightarrow Y}$ (i.e. ${\displaystyle G\,\!}$ and ${\displaystyle G'\,\!}$ agree on their common domain).

If the pair has this property only for a certain codomain ${\displaystyle Y\,\!}$, we say that ${\displaystyle (X,A)\,\!}$ has the homotopy extension property with respect to ${\displaystyle Y\,\!}$.

Visualisation

The homotopy extension property is depicted in the following diagram

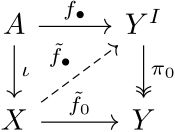
If the above diagram (without the dashed map) commutes (this is equivalent to the conditions above), then pair (X,A) has the homotopy extension property if there exists a map ${\displaystyle {\tilde {f}}_{\bullet }}$ which makes the diagram commute. By currying, note that homotopies expressed as maps ${\displaystyle {\tilde {f}}_{\bullet }\colon X\to Y^{I}}$ are in natural bijection with expressions as maps ${\displaystyle {\tilde {f}}_{\bullet }\colon X\times I\to Y}$.

Note that this diagram is dual to (opposite to) that of the homotopy lifting property; this duality is loosely referred to as Eckmann–Hilton duality.

Properties

• If ${\displaystyle X\,\!}$ is a cell complex and ${\displaystyle A\,\!}$ is a subcomplex of ${\displaystyle X\,\!}$, then the pair ${\displaystyle (X,A)\,\!}$ has the homotopy extension property.
• A pair ${\displaystyle (X,A)\,\!}$ has the homotopy extension property if and only if ${\displaystyle (X\times \{0\}\cup A\times I)}$ is a retract of ${\displaystyle X\times I.}$

Other

If ${\displaystyle (X,A)}$ has the homotopy extension property, then the simple inclusion map ${\displaystyle \iota \colon A\to X}$ is a cofibration.

In fact, if you consider any cofibration ${\displaystyle \iota \colon Y\to Z}$, then we have that ${\displaystyle \mathbf {\mathit {Y}} }$ is homeomorphic to its image under ${\displaystyle \iota }$. This implies that any cofibration can be treated as an inclusion map, and therefore it can be treated as having the homotopy extension property.

See also

• Homotopy lifting property

References

• Hatcher, Allen (2002). Algebraic Topology. Cambridge University Press. ISBN 0-521-79540-0.
• "Homotopy extension property". PlanetMath.