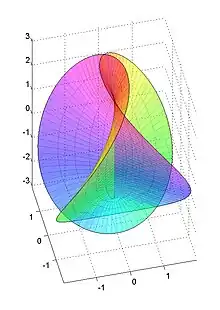
Henneberg surface.
In differential geometry, the Henneberg surface is a non-orientable minimal surface[1] named after Lebrecht Henneberg.
It has parametric equation
and can be expressed as an order-15 algebraic surface.[2] It can be viewed as an immersion of a punctured projective plane.[3] Up until 1981 it was the only known non-orientable minimal surface.[4]
The surface contains a semicubical parabola ("Neile's parabola") and can be derived from solving the corresponding Björling problem.[5][6]
References
- ↑ L. Henneberg, Über salche minimalfläche, welche eine vorgeschriebene ebene curve sur geodätishen line haben, Doctoral Dissertation, Eidgenössisches Polythechikum, Zürich, 1875
- ↑ Weisstein, Eric W. "Henneberg's Minimal Surface." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/HennebergsMinimalSurface.html
- ↑ Ulrich Dierkes, Stefan Hildebrandt, Friedrich Sauvigny, Minimal Surfaces, Volume 1. Springer 2010
- ↑ M. Elisa G. G. de Oliveira, Some New Examples of Nonorientable Minimal Surfaces, Proceedings of the American Mathematical Society, Vol. 98, No. 4, Dec., 1986
- ↑ L. Henneberg, Über diejenige minimalfläche, welche die Neil'sche Paralee zur ebenen geodätischen line hat, Vierteljschr Natuforsch, Ges. Zürich 21 (1876), 66–70.
- ↑ Kai-Wing Fung, Minimal Surfaces as Isotropic Curves in C3: Associated minimal surfaces and the Björling's problem. MIT BA Thesis. 2004 http://ocw.mit.edu/courses/mathematics/18-994-seminar-in-geometry-fall-2004/projects/main1.pdf
Further reading
- E. Güler; Ö. Kişi; C. Konaxis, Implicit equations of the Henneberg-type minimal surface in the four-dimensional Euclidean space. Mathematics 6(12), (2018) 279. doi:10.3390/math6120279.
- E. Güler; V. Zambak, Henneberg's algebraic surfaces in Minkowski 3-space. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 68(2), (2019) 1761–1773. doi:10.31801/cfsuasmas.444554.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
