In geometry, the demiregular tilings are a set of Euclidean tessellations made from 2 or more regular polygon faces. Different authors have listed different sets of tilings. A more systematic approach looking at symmetry orbits are the 2-uniform tilings of which there are 20. Some of the demiregular ones are actually 3-uniform tilings.
20 2-uniform tilings
Grünbaum and Shephard enumerated the full list of 20 2-uniform tilings in Tilings and Patterns, 1987:
cmm, 2*22 (44; 33.42)1 |
cmm, 2*22 (44; 33.42)2 |
pmm, *2222 (36; 33.42)1 |
cmm, 2*22 (36; 33.42)2 |
cmm, 2*22 (3.42.6; (3.6)2)2 |
pmm, *2222 (3.42.6; (3.6)2)1 |
pmm, *2222 ((3.6)2; 32.62) |
p4m, *442 (3.12.12; 3.4.3.12) |
p4g, 4*2 (33.42; 32.4.3.4)1 |
pgg, 2× (33.42; 32.4.3.4)2 |
p6m, *632 (36; 32.62) |
p6m, *632 (36; 34.6)1 |
p6, 632 (36; 34.6)2 |
cmm, 2*22 (32.62; 34.6) |
p6m, *632 (36; 32.4.3.4) |
p6m, *632 (3.4.6.4; 32.4.3.4) |
p6m, *632 (3.4.6.4; 33.42) |
p6m, *632 (3.4.6.4; 3.42.6) |
p6m, *632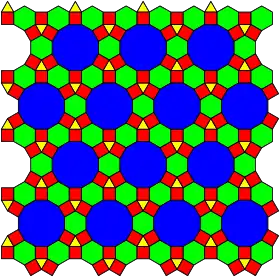 (4.6.12; 3.4.6.4) |
p6m, *632 (36; 32.4.12) |
Ghyka's list (1946)
Ghyka lists 10 of them with 2 or 3 vertex types, calling them semiregular polymorph partitions.[1]
 |
 |
 | ||
| Plate XXVII No. 12 4.6.12 3.4.6.4 |
No. 13 3.4.6.4 3.3.3.4.4 |
No. 13 bis. 3.4.4.6 3.3.4.3.4 |
No. 13 ter. 3.4.4.6 3.3.3.4.4 |
Plate XXIV No. 13 quatuor. 3.4.6.4 3.3.4.3.4 |
 |
 | |||
| No. 14 33.42 36 |
Plate XXVI No. 14 bis. 3.3.4.3.4 3.3.3.4.4 36 |
No. 14 ter. 33.42 36 |
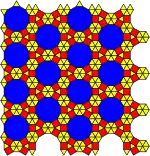
No. 15 3.3.4.12 36 |
Plate XXV No. 16 3.3.4.12 3.3.4.3.4 36 |
Steinhaus's list (1969)
Steinhaus gives 5 examples of non-homogeneous tessellations of regular polygons beyond the 11 regular and semiregular ones.[2] (All of them have 2 types of vertices, while one is 3-uniform.)
| 2-uniform | 3-uniform | |||
|---|---|---|---|---|
 |
 |
 |
 |
 |
| Image 85 33.42 3.4.6.4 |
Image 86 32.4.3.4 3.4.6.4 |
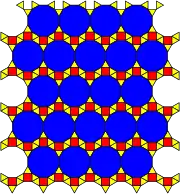
Image 87 3.3.4.12 36 |
Image 89 33.42 32.4.3.4 |
Image 88 3.12.12 3.3.4.12 |
Critchlow's list (1970)
Critchlow identifies 14 demi-regular tessellations, with 7 being 2-uniform, and 7 being 3-uniform.
He codes letter names for the vertex types, with superscripts to distinguish face orders. He recognizes A, B, C, D, F, and J can't be a part of continuous coverings of the whole plane.
| A (none) | B (none) | C (none) | D (none) | E (semi) | F (none) | G (semi) | H (semi) | J (none) | K (2) (reg) | |
|---|---|---|---|---|---|---|---|---|---|---|
3.7.42 |
3.8.24 |
3.9.18 |
3.10.15 |
3.12.12 |
4.5.20 |
4.6.12 |
4.8.8 |
5.5.10 |
63 | |
| L1 (demi) | L2 (demi) | M1 (demi) | M2 (semi) | N1 (demi) | N2 (semi) | P (3) (reg) | Q1 (semi) | Q2 (semi) | R (semi) | S (1) (reg) |
3.3.4.12 |
3.4.3.12 |
3.3.6.6 |
3.6.3.6 |
3.4.4.6 |
3.4.6.4 |
44 |
3.3.4.3.4 |
3.3.3.4.4 |
3.3.3.3.6 |
36 |
| 1 | 2 | 4 | 6 | 7 | 10 | 14 |
|---|---|---|---|---|---|---|
 (3.12.12; 3.4.3.12) |
 (36; 32.4.12) |
 (4.6.12; 3.4.6.4) |
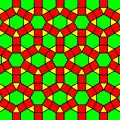
 ((3.6)2; 32.62) |
 (3.4.6.4; 32.4.3.4) |
 (36; 32.4.3.4) |
 (3.4.6.4; 3.42.6) |
| E+L2 | L1+(1) | N1+G | M1+M2 | N2+Q1 | Q1+(1) | N1+Q2 |
| 3 | 5 | 8 | 9 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|
| (3.3.4.3.4; 3.3.4.12, 3.4.3.12) | (36; 3.3.4.12; 3.3.4.3.4) | (3.3.4.3.4; 3.3.3.4.4, 4.3.4.6) | (36, 3.3.4.3.4) | (36; 3.3.4.3.4, 3.3.3.4.4) | (36; 3.3.4.3.4; 3.3.3.4.4) | (3.4.6.4; 3.42.6) |
| L1+L2+Q1 | L1+Q1+(1) | N1+Q1+Q2 | Q1+(1) | Q1+Q2+(1) | Q1+Q2+(1) | N1+N2 |
| Claimed Tilings and Duals | ||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
References
- Ghyka, M. The Geometry of Art and Life, (1946), 2nd edition, New York: Dover, 1977.
- Keith Critchlow, Order in Space: A design source book, 1970, pp. 62–67
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. pp. 35–43
- Steinhaus, H. Mathematical Snapshots 3rd ed, (1969), Oxford University Press, and (1999) New York: Dover
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman. ISBN 0-7167-1193-1. p. 65
- Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.
- In Search of Demiregular Tilings, Helmer Aslaksen
External links
- Weisstein, Eric W. "Demiregular tessellation". MathWorld.
- n-uniform tilings Brian Galebach