|
Probability density function 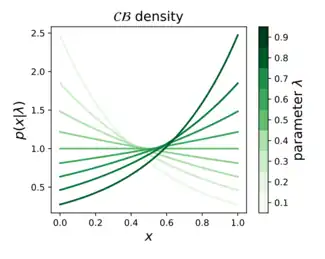 | |||
| Notation | |||
|---|---|---|---|
| Parameters | |||
| Support | |||
|
where | |||
| CDF | |||
| Mean | |||
| Variance | |||
In probability theory, statistics, and machine learning, the continuous Bernoulli distribution[1][2][3] is a family of continuous probability distributions parameterized by a single shape parameter , defined on the unit interval , by:
The continuous Bernoulli distribution arises in deep learning and computer vision, specifically in the context of variational autoencoders,[4][5] for modeling the pixel intensities of natural images. As such, it defines a proper probabilistic counterpart for the commonly used binary cross entropy loss, which is often applied to continuous, -valued data.[6][7][8][9] This practice amounts to ignoring the normalizing constant of the continuous Bernoulli distribution, since the binary cross entropy loss only defines a true log-likelihood for discrete, -valued data.
The continuous Bernoulli also defines an exponential family of distributions. Writing for the natural parameter, the density can be rewritten in canonical form: .
Related distributions
Bernoulli distribution
The continuous Bernoulli can be thought of as a continuous relaxation of the Bernoulli distribution, which is defined on the discrete set by the probability mass function:
where is a scalar parameter between 0 and 1. Applying this same functional form on the continuous interval results in the continuous Bernoulli probability density function, up to a normalizing constant.
Beta distribution
The Beta distribution has the density function:
which can be re-written as:
where are positive scalar parameters, and represents an arbitrary point inside the 1-simplex, . Switching the role of the parameter and the argument in this density function, we obtain:
This family is only identifiable up to the linear constraint , whence we obtain:
corresponding exactly to the continuous Bernoulli density.
Exponential distribution
An exponential distribution restricted to the unit interval is equivalent to a continuous Bernoulli distribution with appropriate parameter.
Continuous categorical distribution
The multivariate generalization of the continuous Bernoulli is called the continuous-categorical.[10]
References
- ↑ Loaiza-Ganem, G., & Cunningham, J. P. (2019). The continuous Bernoulli: fixing a pervasive error in variational autoencoders. In Advances in Neural Information Processing Systems (pp. 13266-13276).
- ↑ PyTorch Distributions. https://pytorch.org/docs/stable/distributions.html#continuousbernoulli
- ↑ Tensorflow Probability. https://www.tensorflow.org/probability/api_docs/python/tfp/edward2/ContinuousBernoulli Archived 2020-11-25 at the Wayback Machine
- ↑ Kingma, D. P., & Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
- ↑ Kingma, D. P., & Welling, M. (2014, April). Stochastic gradient VB and the variational auto-encoder. In Second International Conference on Learning Representations, ICLR (Vol. 19).
- ↑ Larsen, A. B. L., Sønderby, S. K., Larochelle, H., & Winther, O. (2016, June). Autoencoding beyond pixels using a learned similarity metric. In International conference on machine learning (pp. 1558-1566).
- ↑ Jiang, Z., Zheng, Y., Tan, H., Tang, B., & Zhou, H. (2017, August). Variational deep embedding: an unsupervised and generative approach to clustering. In Proceedings of the 26th International Joint Conference on Artificial Intelligence (pp. 1965-1972).
- ↑ PyTorch VAE tutorial: https://github.com/pytorch/examples/tree/master/vae.
- ↑ Keras VAE tutorial: https://blog.keras.io/building-autoencoders-in-keras.html.
- ↑ Gordon-Rodriguez, E., Loaiza-Ganem, G., & Cunningham, J. P. (2020). The continuous categorical: a novel simplex-valued exponential family. In 36th International Conference on Machine Learning, ICML 2020. International Machine Learning Society (IMLS).