

The Apache Point Observatory Lunar Laser-ranging Operation, or APOLLO,[1] is a project at the Apache Point Observatory in New Mexico.[2] It is an extension and advancement of previous Lunar Laser Ranging experiments, which use retroreflectors on the Moon to track changes in lunar orbital distance and motion.
Using telescopes on Earth, the reflectors on the Moon, and accurate timing of laser pulses, scientists were able to measure and predict the orbit of the Moon to a precision of a few centimeters by the early 2000s. This precision provides the best known test of many aspects of our theories of gravity. APOLLO improves this precision even further, measuring the distance between the Moon and Earth to within a few millimeters. Using this information, scientists will be able to further test various aspects of gravity, such as: determining whether the Earth and the Moon react the same to gravity despite their different compositions, investigating the predictions of Einstein with respect to the energy content of the Earth and the Moon and how they react to gravity, and evaluating whether general relativity correctly predicts the motion of the Moon.
The APOLLO collaboration built their apparatus on the 3.5 meter telescope at Apache Point in southern New Mexico. By using a large telescope at a site with good atmospheric seeing, the APOLLO collaboration gets much stronger reflections than any existing facilities. APOLLO records approximately one returned laser photon per pulse, as opposed to the roughly 0.01 photon-per-pulse average experienced by previous LLR facilities. The stronger return signal from APOLLO translates to much more accurate measurements.
History and motivation
High precision Lunar Laser Ranging (LLR) started soon after the Apollo 11 astronauts left the first retroreflector on the Moon.[3] Additional reflectors were left by the Apollo 14 and Apollo 15 astronauts, and two French-built reflector arrays were placed on the Moon by the Soviet Luna 17 (Lunokhod 1) and Luna 21 (Lunokhod 2) lunar rover missions. Over the years since, many groups and experiments have used this technique to study the behavior of the Earth–Moon system, investigating gravitational and other effects.[4][5]
For the first few years of the Lunar Laser Ranging Experiment, the distance between the observatory and the reflectors could be measured to an accuracy of about 25 cm. Improved techniques and equipment lead to accuracies of 12–16 cm until about 1984. Then McDonald Observatory built a special purpose system (MLRS) just for ranging, and achieved accuracies of roughly 3 cm in the mid-to-late 1980s. In the early 1990s a French LLR system at the Observatoire de la Côte d’Azur (OCA) started operation, with similar precision.[2]
The McDonald and OCA stations are collecting data that is about as good as possible, given the number of photons that they collect back from the reflectors. Although minor improvements are possible, getting significantly better data requires a larger telescope and a better site. This is the basic goal of the APOLLO collaboration.
The APOLLO laser has been operational since October 2005, and routinely achieves millimeter-level range accuracy between the Earth and the Moon.[6]
Science goals
The goal of APOLLO is to push LLR into the millimeter range precision, which then translates directly into an order-of-magnitude improvement in the determination of fundamental physics parameters. Specifically, assuming improvements of a factor of ten over prior measurements,[7][8] APOLLO will test:
- the Weak Equivalence Principle (WEP) to a part in 1014,
- the Strong Equivalence Principle (SEP) to a few parts in 105,
- de Sitter relativistic precession to a few parts in 104, and
- the time variation of the gravitational constant G to a part in 1013 per year.
Tests of the Equivalence Principles
The Weak Equivalence Principle says that all objects fall the same way in a gravity field, no matter what they are made of. The Earth and the Moon have very different compositions—for example, the Earth has a large iron core, but the Moon does not. Furthermore, both are in orbit around the Sun, meaning that they are both falling towards the Sun at all times, even as they revolve around each other. If the Earth and the Moon were affected differently by the gravity of the Sun, this would directly affect the orbit of the Moon around the Earth. As closely as scientists can measure, the orbit of the Moon is just as predicted from assuming that gravity acts the same on each — to within 1 part in 1013, the Earth and the Moon fall towards the Sun in exactly the same way, despite their different compositions. APOLLO will lead to even tighter limits.
The Strong Equivalence Principle, according to Albert Einstein's general relativity, predicts that the mass of any object consists of two parts – the mass of the atoms themselves, plus the mass of the energy that holds the object together. The question is whether the energy portion of mass contributes to measured gravity of the object, or to the inertia. In general relativity, the self-energy affects both the gravitational field and inertia, and does so equally.
Other modern theories, such as string theory, quintessence, and various forms of quantum gravity, almost all predict a violation of the Strong Equivalence Principle at some level. Additionally, many puzzling experimental results, such as galaxy rotation curves that imply the existence of dark matter or supernova observations that imply the existence of dark energy, could also potentially be explained by alternative theories of gravity (see, for example, MOND). Therefore, experimentalists believe it is important to make the most precise measurements of gravity possible, looking for any possible anomalies or confirming Einstein's predictions.
Precise ranging to the Moon can test the SEP since the Earth and the Moon have a different fraction of their mass in the energy component. Precision measurements are needed since this component is very small – if mE is the self energy of the Earth — the energy needed to spread the atoms of the Earth out to infinity against the attraction of gravity — then the mass of the Earth is decreased by about mE/c2 = 4.6×10−10 of the Earth’s total mass. The self energy of the Moon is smaller yet, about 2×10−11 of its mass. (The contribution for any object of laboratory size is negligible, about 10−27, so only measurements of planet-sized or bigger objects would allow this effect to be measured.)[9]
If the Moon revolved around only the Earth, there would be no way to tell what fraction of the Moon's or the Earth's gravity was caused by each form of mass, since only the total can be measured. However, the orbit of the Moon is also strongly affected by the gravity of the Sun – in essence, Earth and Moon are in free fall around the Sun. If the energy portion of mass behaves differently from the conventional portion, then the Earth and the Moon will fall differently toward the Sun, and the orbit of the Moon around the Earth will be affected. For example, suppose the energy part of the mass does affect gravity, but does not affect inertia. Then:
From our perspective on Earth, this would appear as a displacement, or polarization, of the lunar orbit away from the Sun with an amplitude of 13 meters. If the violation went the other way, with the self energy possessing inertial mass but not gravitational mass, the lunar orbit would appear to be polarized toward the Sun by the same amplitude. The calculation of the amplitude is complicated,[10][11][12] but a crude estimate may be derived by multiplying the Earth’s orbital radius of 1.5×1011 m by the 4.6×10−10 contribution to the Earth’s mass from the self-energy to yield 75 meters.[2]
The signature of an EP violation is very simple, depending only on the distance of the Moon from the Sun. This repeats about every 29.5 days, somewhat longer than the time the Moon takes to go around the Earth once, which is 27.3 days. (This difference arises since the Earth moves along its orbit as the Moon goes around, so the Moon has to make a little more than one orbit to get back to the same position relative to the Sun.) This makes EP particularly easy to measure, since many confounding effects such as tides or weather will not repeat at 29.5-day intervals. Unfortunately, there is one effect – radiation pressure acting on the orbit of the Moon – that does repeat each 29.5 days. Fortunately, it is small, less than 4 mm, and fairly easy to model, which allows it to be subtracted out.
Finally, even if the experiments show no effect, there is a tiny theoretical loophole. The measurements show the sum of the WEP and SEP violations. If the experiments show no effect, the most natural explanation is that neither WEP or SEP are violated. But it is conceptually possible that both are violated, and by equal and opposite amounts. This would be an incredible coincidence since WEP and SEP depend on very different and arbitrary properties – the exact composition of the Earth and the Moon, and their self-energies. But this unlikely case cannot be completely ruled out until either other solar system bodies are measured to similar precision, or laboratory experiments reduce the bounds on WEP violations alone.
Variations in the gravitational constant
Existing ranging experiments can measure the constancy of the gravitational constant, G, to about one part in 1012 per year. The expansion rate of the universe is approximately one part in 1010 per year. So if G scaled with the size or expansion of the universe, existing experiments would already have seen this variation. This result can also be viewed as experimental verification of the theoretical result[13][14] that gravitationally bound systems do not partake in the general expansion of the universe. APOLLO will place much tighter bounds on any such variations.
Other tests
At this level of accuracy, general relativity is needed to predict the orbit of the Moon. Current tests measure geodetic precession to a 0.35% level of precision, gravitomagnetism at the 0.1% level, and checks whether gravity behaves as 1/r2 as expected. APOLLO will improve on all these measurements.
Principles of operation
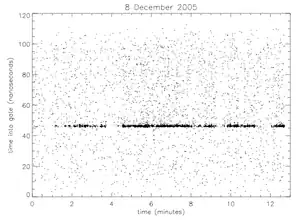
APOLLO is based on measuring the time-of-flight of a short-pulse laser reflected from a distant target—in this case the retroreflector arrays on the Moon. Each burst of light lasts 100 picoseconds (ps).[15] One millimeter in range corresponds to only 6.7 ps of round-trip travel time. However, the retroreflectors on the Moon introduce more than one millimeter of error themselves. They are not usually at an exact right angle to the incoming beam, so the different corner cubes of the retroreflectors are at different distances from the transmitter. This is because the Moon, although it keeps one face to the Earth, does not do so exactly—it wobbles from side to side and up and down, by as much as 10° in magnitude. (See libration.) These librations occur since the Moon rotates at constant speed, but has an elliptical and inclined orbit. This effect may seem small, but it is not only measurable, it forms the largest unknown in finding the range, since there is no way to tell which corner cube reflected each photon. The biggest array, the 0.6 m2 Apollo 15 reflector, can have a corner-to-corner range spread of ≈ 1.2 sin (10°) m, or 210 mm, or about 1.4 ns of round-trip time. The root-mean-square (RMS) range spread is then about 400 ps. To determine the distance to the reflector to 1 mm precision, or 7 ps, by averaging, the measurement needs at least (400/7)2 ≈ 3000 photons. This explains why a much larger system is needed to improve the existing measurements—the pre-APOLLO 2 cm RMS range precision required only about 10 photons, even at the worst-case orientation of the retroreflector array.
APOLLO attacks this problem by using both a bigger telescope and better astronomical seeing. Both are considerably improved over existing systems. Compared to McDonald Observatory ranging station, the Apache Point telescope has a factor of 20 greater light-collecting area. There is also a big gain from better seeing—the APO site and telescope combined can often achieve one arcsecond seeing, compared to the ≈5 arcseconds typical for the previous McDonald Lunar Ranging Station (MLRS). The better seeing helps two ways—it both increases the laser beam intensity on the Moon and reduces the lunar background, since a smaller receiver field-of-view may be used, gathering light from a smaller spot on the Moon. Both effects scale as the inverse square of the seeing, so that the signal-to-noise ratio of the lunar return is inversely proportional to the fourth power of the seeing. APOLLO should therefore gain about 20 (from the bigger telescope) × 25 (for better seeing) = 500 × in return signal strength over MLRS, and additional factor of 25 in signal-to-noise (from fewer stray photons interfering with the desired ones). Likewise APOLLO should get a signal about 50 times stronger than the OCA LLR facility, which has a 1.5 m telescope and seeing of about 3 arcsec.
The increased optical gain brings some problems due to the possibility of getting more than one returned photon per pulse. The most novel component of the APOLLO system is the integrated array of Single-Photon Avalanche Diodes (SPADs) used in the detector. This technology is needed to deal with multiple photon returns within each pulse. Most single photon detectors suffer from "dead time": they cannot detect a photon if it arrives soon after another. This means that if more than one photon comes back in a single pulse, a conventional single-photon detector would only record the arrival time of the first photon. However, the important quantity is the centroid of the time of all returned photons (assuming the pulse and reflectors are symmetrical), so any system that can return multiple photons per pulse must record the arrival times of each photon. In APOLLO, the incoming photons are spread over an array of independent detectors, which reduces the chance that two or more photons hit any one of the detectors.[2]
Modeling station locations
Any laser ranging station, APOLLO included, measures the transit time, and hence the distance, from the telescope to the reflector(s). But for lunar ranging science, what is really wanted is the distance between the center of mass of the Earth and the center of mass of the Moon. To do this, the positions of the telescope, and the reflectors, must be known to comparable precision (a few mm). Since both the telescope and the reflectors are stationary structures, it might seem they could be precisely measured, and then their position would be known thereafter. This assumption is not too bad for the Moon, which is a quiet environment. But for the Earth, the stations move quite a bit on this scale:
- The Earth's polar axis moves and the Earth's rotation is irregular. The polar axis moves due to various causes, some predictable (the Moon exerts a torque on Earth's tidal bulge) and some variable (rocks are rebounding from the last ice age, weather). Weather also affects the Earth's rotation, by moving large masses of water around. These effects, important to many other science projects as well, even have their own agency to keep track of them—the International Earth Rotation and Reference Systems Service.
- The stations move due to tides. The Moon, since it is tidally locked to the Earth, has relatively small and repeatable tides of about 10 cm. The solid Earth has larger tides, oscillating about 35 cm peak-to-peak, every 12 hours.
- The Earth's crust changes in response to long term fluctuations such as post-glacial rebound and loading caused by sediment transport.[16]
- The Earth's short-term weather can also affect the location of the telescope, primarily vertically. Various weather effects can load local regions of the Earth's crust, depressing the crust by a few millimeters. These effects come from the atmosphere (high pressure systems press on the Earth's surface), and the ocean (water piles up on the coast depressing the crust). Ground water fluctuations, caused by rain, can also affect the telescope location.
- The pressure of sunlight pushes the Moon's orbit slightly off center. This is a small effect, about 3.65 mm,[17] but it is particularly important since it mimics the effect of an EP violation.
- Even continental drift must be compensated for.
In addition, the Earth's atmosphere causes an additional delay, since the speed of light is slightly slower through the atmosphere. This amounts to about 1.6 meters when looking straight up at Apache Point. This delay is also affected by weather, primarily atmospheric pressure, which determines just how much air there is above the site.
Since many of these effects are weather-related, and also affect the more common satellite laser ranging, ranging stations traditionally include weather stations, measuring local temperature, pressure, and relative humidity. APOLLO will measure all these, plus measure local gravity very precisely, using a precision gravimeter.[18] This instrument is capable of sensing vertical displacements as small as 0.1 mm, by measuring the change in gravity as the observatory moves closer to or farther from the Earth's center.
Using all these measurements, scientists try to model and predict the exact location of the telescope, and the delays through the atmosphere, so they can compensate for them. The tides are fairly predictable, and the Earth's rotation is measured by the IERS and can be accounted for. Atmospheric delay is fairly well understood, and is dominated by the pressure measurement alone. Early models had uncertainties in the 5–10 mm range for reasonable elevation angles,[19] though more recent efforts have produced a model claiming 3 mm accuracy down to 10 degrees above the horizon, and sub-millimeter performance above 20–30° elevation.[20] The weather is perhaps the biggest error source. Atmospheric loading is estimated from the barometric pressure at the telescope and the average pressure within a 1000 km radius. Ocean loading has been handled strictly by empirical models, and ground water has been largely ignored. APOLLO will probably require improvements in all these models to reach the full accuracy of the measurements.
Discoveries
In April 2010, the APOLLO team announced that, with the aid of photos from the Lunar Reconnaissance Orbiter, they had found the long-lost Lunokhod 1 rover and had received returns from its laser retroreflector.[21][22] By the fall of 2010, the location of the rover had been trilaterated (using range measurements from different points in the Earth's rotation and the Moon's libration) to about a centimeter. The location near the limb of the moon, combined with the ability to range the rover even when it is in sunlight, promises to be particularly useful for determining aspects of the Earth-Moon system.[23]
The APOLLO collaboration has discovered that the optical efficiency of the lunar reflectors decreases at full moon. This effect was not present in measurements from the early 1970s, was visible but not strong in the 1980s, and is now quite significant; the signal is about 10-fold less during a full moon. The cause was suspected to be due to dust on the arrays, leading to temperature gradients, distorting the returned beam.[24] Measurements during the total lunar eclipse of December 2010 confirmed thermal effects as the cause.[25] The sudden cut off and restoration of the light allowed thermal time constants of the effect to be observed.
Status
APOLLO has been up and working to various degrees since October 2005, with science-quality data beginning April 2006. By mid-2011, the status was:[25]
- All 5 reflectors (three Apollo and two Lunokhod) ranged routinely.
- As many as 12 photons in a single pulse (limited by detector – might have been more).
- Sustained rate of about 3 photons per pulse over several minutes. This is about 65 times more photons detected than previous efforts.
- As many as 50,000 return photons detected in a single lunation (during 5 hours total operation).
As of mid-2011, the range precision (per session) was believed to be about 1.8–3.3 mm per reflector,[25] while the orbit of the Moon is being determined to roughly the 15 mm level.[25] The gap between the measurements and the theory could be due to systematic errors in the ranging, insufficient modeling of various conventional effects that become important at this level, or limitations of our theory of gravity. Although it is possible that this discrepancy is due to new physics, the primary suspect is insufficient modeling, since this is known to be both complex and difficult.
To enable APOLLO to improve beyond the part per trillion measurement accuracy level, in 2016 it added a cesium atomic clock and improved calibration system.[26][27] With the new system in place, the possible accuracy can be increased to better than 2 mm.[26]
The new system has confirmed the accuracy of previous measurements. It revealed that the previous estimate of 10 ps of error (corresponding to 1.5 mm of distance uncertainty) attributed to APOLLO's GPS-synchronized oven-controlled crystal oscillator was too low; the true figure was closer to 20 ps (3 mm).[28] However, careful record-keeping allowed the old data to be reanalyzed in light of the new understanding of the clock's variations and most of the accuracy recovered.[28]
By confirming the accuracy of previous measurements, and making new even more accurate measurements, the still unresolved 15–20 mm discrepancy between theory and experiment is now placed more firmly on the theoretical models.
The collaboration
APOLLO is collaboration between: University of California, San Diego (Tom Murphy Principal investigator), University of Washington, Harvard, Jet Propulsion Laboratory, Lincoln Laboratory, Northwest Analysis, Apache Point Observatory, and Humboldt State.
References
- ↑ APOLLO Website. "The Apache Point Observatory Lunar Laser-ranging Operation".
- 1 2 3 4 Murphy Jr., T.W.; Strasburg, J.D.; Stubbs, C.W.; Adelberger, E.G.; Angle, J.; Nordtvedt, K.; et al. (January 2008). "The Apache Point Observatory Lunar LASER-Ranging Operation (APOLLO)" (PDF). Publications of the Astronomical Society of the Pacific. 120 (863): 20–37. arXiv:0710.0890. Bibcode:2008PASP..120...20M. doi:10.1086/526428. S2CID 12695081.
- ↑ "History of Laser Ranging and MLRS". McDonald Observatory.
- ↑ Bender, P. L.; Currie, D. G.; Dicke, R. H.; Eckhardt, D. H.; Faller, J. E.; Kaula, W. M.; et al. (1973). "The Lunar Laser Ranging Experiment". Science. 182 (4109): 229–38. Bibcode:1973Sci...182..229B. doi:10.1126/science.182.4109.229. PMID 17749298. S2CID 32027563.
- ↑ Dickey, J. O.; Bender, P. L.; Faller, J.E.; Newhall, X. X.; Ricklefs, R. L.; Ries, J. G.; et al. (1994). "Lunar Laser Ranging: A Continuing Legacy of the Apollo Program" (PDF). Science. 265 (5171): 482–90. Bibcode:1994Sci...265..482D. doi:10.1126/science.265.5171.482. PMID 17781305. S2CID 10157934.
- ↑ Murphy Jr., TW; Adelberger, EG; Battat, JBR; Hoyle, CD; Johnson, NH; McMillan, RJ; et al. (2012). "APOLLO: millimeter lunar laser ranging" (PDF). Classical and Quantum Gravity. IOP Publishing. 29 (18): 184005. Bibcode:2012CQGra..29r4005M. doi:10.1088/0264-9381/29/18/184005. S2CID 13240200.
- ↑ Williams, J. G.; Newhall, X. X. & Dickey, J. O. (1996). "Relativity parameters determined from lunar laser ranging". Physical Review D. 53 (12): 6730–6739. Bibcode:1996PhRvD..53.6730W. doi:10.1103/PhysRevD.53.6730. PMID 10019959.
- ↑ Anderson, J. D. & Williams, J. G. (2001). "Long-Range Tests of the Equivalence Principle". Classical and Quantum Gravity. 18 (13): 2447–2456. Bibcode:2001CQGra..18.2447A. doi:10.1088/0264-9381/18/13/307. S2CID 250861959.
- ↑ Clifford M. Will. "The Confrontation between General Relativity and Experiment". Max Planck Society. Archived from the original on 2016-03-03. Retrieved 2019-05-24., section 3.6.
- ↑ Nordtvedt, K. (1995). "The Relativistic Orbit Observables in Lunar Laser Ranging". Icarus. 114 (1): 51–62. Bibcode:1995Icar..114...51N. doi:10.1006/icar.1995.1042.
- ↑ Damour, T. & Vokrouhlický, D. (1996). "Equivalence Principle and the Moon". Physical Review D. 53 (8): 4177–4201. arXiv:gr-qc/9507016. Bibcode:1996PhRvD..53.4177D. doi:10.1103/PhysRevD.53.4177. PMID 10020415. S2CID 29854472.
- ↑ Müller, J. & Nordtvedt, K. (1998). "Lunar laser ranging and the equivalence principle signal". Physical Review D. 58 (200): 062001. Bibcode:1998PhRvD..58f2001M. doi:10.1103/PhysRevD.58.062001.
- ↑ Einstein, Albert, and Ernst G. Straus (1945). "The influence of the expansion of space on the gravitation fields surrounding the individual stars". Reviews of Modern Physics. 17.2 (3): 120–124. Bibcode:1945RvMP...17..120E. doi:10.1103/RevModPhys.17.120.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Noerdlinger, P. D.; Petrosian, V. (1971). "The Effect of Cosmological Expansion on Self-Gravitating Ensembles of Particles". Astrophysical Journal. 168: 1. Bibcode:1971ApJ...168....1N. doi:10.1086/151054.
- ↑ Murphy, T. "The Basics of Lunar Ranging". UCSD.
- ↑ JPL/NASA. "NASA says glacial sediments adding to Louisiana coast's sinking". Spaceflight Now.
- ↑ David Vokrouhlický (1997). "A Note on the Solar Radiation Perturbations of Lunar Motion". Icarus. 126 (2): 293–300. Bibcode:1997Icar..126..293V. doi:10.1006/icar.1996.5652. S2CID 122769233.
- ↑ "Superconducting Gravity Sensors". GWR Instruments. Archived from the original on 2019-03-02. Retrieved 2019-03-13.
- ↑ Marini, J. W. & Murray, C. W. Jr. (1973). "Correction of Laser Range Tracking Data for Atmospheric Refraction at Elevation Angles Above 10 Degrees" (PDF). NASA Technical Report X-591-73-351.
- ↑ Pavlis, E. C. & Mendes, V. B. (2000). "Improved Mapping Functions for Atmospheric Refraction Corrections for LR: Preliminary Validation Results". 12th International Workshop on Laser Ranging, Matera, Italy.
- ↑ Klotz, Irene (27 April 2010). "Lost and Found: Soviet Lunar Rover". Seeker. Retrieved 2017-07-09.
- ↑ Coulter, Dauna (3 June 2010). "Old Moon Rover Beams Surprising Laser Flashes to Earth". Science@NASA. Retrieved 2017-07-09.
- ↑ Murphy Jr., T.W.; Adelberger, E.G.; Battat, J.B.R.; Hoyle, C.D.; Johnson, N.H.; McMillan, R.J.; et al. (February 2011). "Laser Ranging to the Lost Lunokhod~1 Reflector". Icarus. 211 (2): 1103–1108. arXiv:1009.5720. Bibcode:2011Icar..211.1103M. doi:10.1016/j.icarus.2010.11.010. S2CID 11247676.
- ↑ Murphy Jr., T.W.; Adelberger, E.G.; Battat, J.B.R.; Hoyle, C.D.; McMillan, R.J.; Michelsen, E.L.; et al. (July 2010). "Long-term degradation of optical devices on the Moon" (PDF). Icarus. 208 (1): 31–35. arXiv:1003.0713. Bibcode:2010Icar..208...31M. doi:10.1016/j.icarus.2010.02.015. S2CID 15312857.
- 1 2 3 4 Murphy, Thomas (19 May 2011). APOLLO Status Update (PDF). 17th International Workshop on Laser Ranging. Bad Kötzting, Germany.
- 1 2 Adelberger, E.G.; Battat, J.B.R.; Birkmeier, K.J.; Colmenares, N.R.; Davis, R.; Hoyle, C.D.; Huang, L.R.; McMillan, R.J.; Murphy Jr., T.W.; Schlerman, E.; Skrobol, C.; Stubbs, C.W.; Zach, A. (29 June 2017). "An absolute calibration system for millimeter-accuracy APOLLO measurements". Classical and Quantum Gravity. 34 (24): 245008. arXiv:1706.09550. Bibcode:2017CQGra..34x5008A. doi:10.1088/1361-6382/aa953b. S2CID 9249369.
- ↑ Battat, J.B.R.; Huang, L.R.; Schlerman, E.; Murphy, Jr, T.W.; Colmenares, N.R.; Davis, R. (1 July 2017). "Timing calibration of the APOLLO experiment". arXiv:1707.00204 [astro-ph.IM].
{{cite arXiv}}: CS1 maint: multiple names: authors list (link) - 1 2 Liang, Y.; Murphy Jr., T.W.; Colmenares, N.R.; Battat, J.B.R. (28 Jun 2017). "APOLLO clock performance and normal point corrections". Classical and Quantum Gravity. 34 (24): 245009. arXiv:1706.09421. Bibcode:2017CQGra..34x5009L. doi:10.1088/1361-6382/aa953c. S2CID 31927794.
External links
- What Neil & Buzz Left on the Moon NASA description of the basics of Lunar Laser Ranging
- Main web page for the Apache Point Lunar Laser Ranging Project