An algebraic Petri net (APN) is an evolution of the well known Petri net in which elements of user defined data types (called algebraic abstract data types (AADT)[1]) replace black tokens. This formalism can be compared to coloured Petri nets (CPN)[2] in many aspects. However, in the APN case, the semantics of the data types is given by an axiomatization enabling proofs and computations on it.
Algebraic Petri nets[3] were invented by Jacques Vautherin in 1985 in his PhD thesis and later improved by Wolfang Reisig.[4]
The formalism has two aspects :
- The control part which is handled by a Petri net.
- The data part which is handled by one or many AADTs.
AADT can be themselves split in two parts:
- The signature (Sort and Ops in the example below) which gives the valid constants and operations of the term algebra.
- The axiomatization (Axioms in the example below) which gives the semantics of the operations described in the signature part.
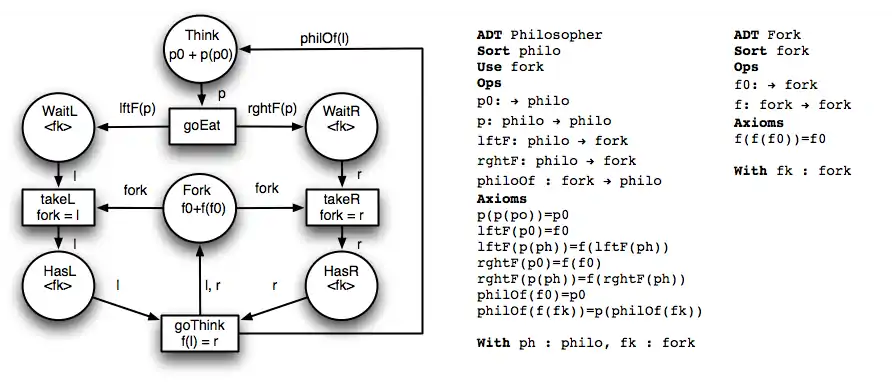
The following picture describes an algebraic Petri net model of the "dining philosophers problem". There are two AADT in this model, one for the forks algebra, one for the philosophers algebra. Please note that the philosophers AADT uses the fork AADT. Since all philosophers can take their left fork without taking their right fork, executing this model can result in a deadlock.
The control part is composed of :
- Places contain multiset (bags) of tokens. Those tokens are elements of a term algebra built upon the signature of the AADT (in the example, terms that represent either a philosopher or a fork). Each place contains one and only one multiset of terms, the place is typed by its multiset.
- Arcs can be labeled with multisets of either closed or free terms. Again terms are built from the AADT signature.
- Transitions are events that can be fired whenever there are enough resources (namely enough tokens in the input places to satisfy all the input arcs) and the guard (firing conditions) of the transition holds. Then the produced tokens are put in the target places of the output arcs. Usually term rewriting[5] is used for the operational semantics in order to check if conditions hold and to compute output terms.
In the example below only transition goEat is firable at the beginning. One goEat has been fired, takeL and takeR are also enabled and thus can also be fired.
Algebraic Petri nets are the basic formalism of more advanced ones such as CO-OPN.
References
- ↑ Ehrig, H. and Mahr, B. 1985 Fundamentals of Algebraic Specification I. Springer-Verlag New York, Inc.
- ↑ K. Jensen. Coloured Petri Nets. Springer, Berlin, 1996.
- ↑ Jacques Vautherin: Parallel systems specifications with Coloured Petri nets and algebraic specifications. European Workshop on Applications and Theory of Petri Nets 1986: 293-308
- ↑ Wolfgang Reisig: Petri Nets and Algebraic Specifications. Theor. Comput. Sci. 80(1): 1-34 (1991)
- ↑ Dick, A. J. and Watson, P. 1991. Order-sorted term rewriting. Comput. J. 34, 1 (Feb. 1991), 16-19.
Further reading
- Vautherin, Jacques (1985). Un Modèle Algébrique, Basé sur les Réseaux de Petri, pour l'Etude des Systèmes Paralleles. These de Docteur Ingenieur, Univ. de Paris-Sud, Centre d'Orsay.
- Jensen, Kurt. Coloured Petri Nets. Springer Verlag. ISBN 3-540-62867-3.