The first step to understanding linear regression is to make sure you understand linear correlation.
Regression examines the relationship between two variables by determining the line of best fit (on a scatterplot). The properties of this line of best fit are determined as the slope (b) and where it touches the Y-axis (a).
Regression involves:
- A predictor (X) variable, or an independent variable (IV), shown on the X-axis
- An outcome (Y) variables, or a dependent variable (DV), shown on the Y-axis
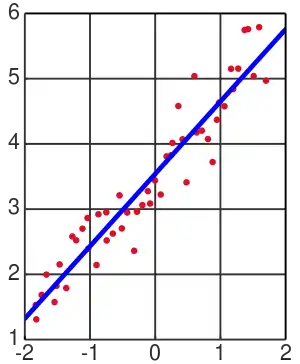
Example of a line of best fit for a linear regression (i.e., one dependent and one independent variable).
The generic equation for a simple linear regression is:
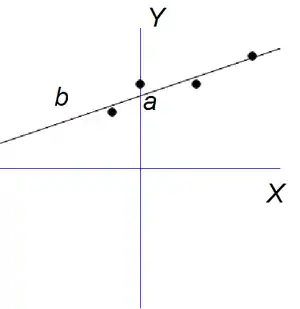
Linear regression variables and co-efficients indicated on a scatterplot with line of best fit.
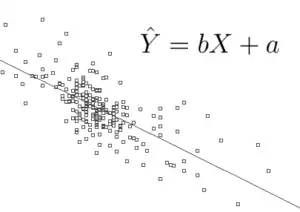
Linear regression scatterplot with line of best fit and generic linear regression formula.
See also
- Linear regression (Wikipedia)
- Multiple linear regression
This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.