Set theory

Type classification: this is a lesson resource.

Educational level: this is a tertiary (university) resource.

Wikibooks has more on the topic of Set theory.

Basic Definition

The term "set" can be thought as a well-defined collection of objects. In set theory, These objects are often called "elements".

We usually use capital letters for the sets, and lowercase letters for the elements.
If an element $a$ belongs to a set $A$ , we can say that " $a$ is a member of the set $A$ ", or that " $a$ is in $A$ ", or simply write $a\in A$ .
Similarly, if $a$ is not in $A$ , we would write $a\notin A$ .

(Example) $x\in \mathbb {R}$ . In this case, $x$ is the element and $\mathbb {R}$ is the set of all real numbers.

Notation

Example of a common notation style for the definition of a set:

$S$ is a set
$P(x)$ is a property (The elements of $S$ may or may not satisfy this property)
Set $A$ can be defined by writing...

$A=\{x\in S\mid P(x)\}$

This would read as "the set of all $x$ in $S$ ,such that $P$ of $x$ ."

Elements

There are two ways that we could show which elements are members of a set: by listing all the elements, or by specifying a rule which leaves no room for misinterpretation. In both ways we will use curly braces to enclose the elements of a set. Say we have a set $A$ that contains all the positive integers that are smaller than ten. In this case we would write $A=\{1,2,3,4,5,6,7,8,9\}$ . We could also use a rule to show the elements of this set, as in $A=\{a:{\text{ }}a{\text{ positive integer less than 10}}\}$ .

In a set, the order of the elements is irrelevant, as is the possibility of duplicate elements. For example, we write $X=\{1,2,3\}$ to denote a set $X$ containing the numbers 1, 2 and 3. Or, $X=\{1,2,3\}=\{3,2,1\}=\{1,1,2,3,3\}$ .

Subsets

A is a subset of B.

\left(A\subseteq B\right)

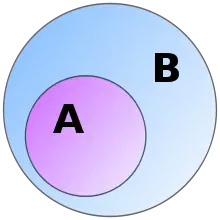
Formal universal conditional statement: "set A is a subset of a set B"

$A\subseteq B\Leftrightarrow \forall x$ , if $x\in A$ , then $x\in B.$

Negation:

$A\nsubseteq B\Leftrightarrow \exists x$ such that $x\in A$ and $x\notin B.$

If and only if: 
    for all  $x$ :
        If: ( $x$  is an element of A)
        then: ( $x$  is an element of B)
then: 
    set A is a subset of set B

Truth Table Example:

$x\in A$	$x\in B.$	if $x\in A$ , then $x\in B.$	$x\in A$ and
1	1	1	0
1	0	0	1
0	1	1	0
0	0	1	0

A proper subset of a set is a subset that is not equal to its containing set. Thus

A is a proper subset of B $\iff$

Set Identities

Let all sets referred to below be subsets of a universal set U.

(a) A ∪ ∅ = A and (b) A ∩ U = A.

5. Complement Laws:

(a) A ∪ A c = U and (b) A ∩ A c = ∅.

6. Double Complement Law:

(A c ) c = A.

7. Idempotent Laws:

(a) A ∪ A = A and (b) A ∩ A = A.

8. Universal Bound Laws:

(a) A ∪ U = U and

(b) A ∩ ∅ = ∅.

$A\cap U=A$	$A\cap U=A$

Identity

For all sets A

Identity Laws:

$A\cup \emptyset =A$

$A\cap U=A$	$A\cap U=A$

Complement Laws:

$A\cup A^{c}=U$

$A\cap A^{c}=\emptyset$

Double Complement Law:

\left(A^{c}\right)^{c}=A

Idempotent Laws:

A\cup A=A

$A\cap A=A$

Universal Bound Laws:

Identity	For all sets A and B
Commutative Laws:	$A\cup B=B\cup A$ $A\cap B=B\cap A$

2. Associative Laws: For all sets A, B, and C,

(a) (A ∪ B) ∪ C = A ∪ (B ∪ C) and

(b) (A ∩ B) ∩ C = A ∩ (B ∩ C).

3. Distributive Laws: For all sets, A, B, and C,

(a) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) and

(b) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).

For all sets A and B,

De Morgan’s Laws:

(a) (A ∪ B) c = A c ∩ B c and (b) (A ∩ B) c = A c ∪ B c .

Absorption Laws:

(a) A ∪ (A ∩ B) = A and (b) A ∩ (A ∪ B) = A.

Set Difference Law:

A − B = A ∩ B c .

Complements of U and ∅:

$U^{c}=\emptyset$
$\emptyset ^{c}=U$

Cardinality

The cardinality of a set is the number of elements in the set. The cardinality of a set $A$ is denoted $|A|$

Types of Sets by Cardinality

A set can be classified as finite, countable, or uncountable.

Finite Sets are sets that have finitely many elements, $A=\{1,2,3\}$ is a finite set of cardinality 3.
Countable Sets are sets that have as many elements as the set of natural numbers, $|\mathbb {Q} |=|\mathbb {N} |$ so the set of rational numbers is countable.
Uncountable Sets are sets that have more elements than the set of natural numbers, $|\mathbb {R} |>|\mathbb {N} |$ so the set of real numbers is uncountable.

Common Sets of Numbers

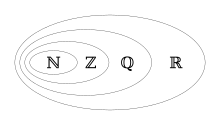
Diagram to demonstrate the number systems ℝ, ℚ, ℤ and ℕ as sub-sets of each other.

$\mathbb {N}$ is the set of Naturals
$\mathbb {Z}$ is the set of Integers
$\mathbb {Q}$ is the set of Rationals
$\mathbb {C}$ is the set of Complex Numbers

Partitions of Sets

In many applications of set theory, sets are divided up into non-overlapping (or disjoint) pieces. Such a division is called a partition.

Two sets are called disjoint if, and only if, they have no elements in common.

A and B are disjoint ⇔ A ∩ B = ∅.

Sets $A_{1},A_{2},A_{3},\ldots$ are mutually disjoint (or pairwise disjoint or nonoverlapping)

if, and only if, no two sets $A_{i}$ and $A_{j}$ with distinct subscripts have any elements in

common. More precisely, for all $i,j=1,2,3,\ldots$

$A_{i}\cap A_{j}=\emptyset$ whenever $i\not =j$ .

Power Sets

The power set of a set A is all possible subsets of A, including A itself and the empty set. Which can be represented:

P_{(A)}=\{\emptyset ,\{1\},\{2\},\ldots \}

For the set $A=\{1,2,3\}$

P_{(A)}=\{\emptyset ,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}\}

Learning resources

Wikiversity

Introduction_to_set_theory/Lecture_1

Wikipedia

Set theory category

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.