In multiple linear regression (MLR), there are two or more independent or predictor variable (IV) and one dependent or response variable (DV).
A correlation (r) indicates the linear relationship between an IV and a DV.
A semi-partial correlation (sr) indicates the unique relation between an IV and the DV. An sr is the variance in a DV explained by an IV and only that IV (i.e., it does not included variance in a DV explained by other IVs).
This is Venn diagram represents the variance, rs, and srs involved in an MLR analysis.
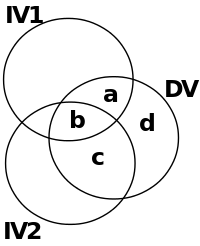
Question 1: Which areas represent the squared semi-partial correlations between the IVs and DV?
Answer: a and c
Question 2: What do the other labelled areas represent? Answer:
- a = semi-partial correlation between IV1 and DV (with the effect of IV2 removed)
- b = variance in the DV which is explained by both IV1 and IV2
- c = semi-partial correlation between IV2 and DV (with the effect of IV1 removed)
- d = variance in DV which is not explained by IV1 and IV2
What are semi-partial correlations useful for?
In MLR, square the sr for each IV, to get the semi-partial correlations squared (sr2).
The sr2s provide the percentage of variance in the DV which is uniquely associated with each IV.
Add the sr2 values to get the percentage of variance in the DV which is uniquely explained by the IVs.
R2s (total percentage of variance explained) minus the total of the sr2s equals the percentage of variance explained by the relationship between predictors.
See also
- Correlation
- Multiple linear regression
- Partial correlation (Wikipedia)