This is a techniques for dealing with more complex circuit arrangements. Consider this problem: 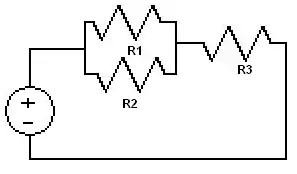 Based on what we have learned in the previous lectures this circuit is solvable. All we have to do is follow the reduction algorithm:
Based on what we have learned in the previous lectures this circuit is solvable. All we have to do is follow the reduction algorithm:
- 1 If any two or more resistors are in series combine them together and then replace it with an equivalent resistance.
- 2 If any two or more resistors are in parallel combine them together and then replace it with an equivalent resistance.
- 3 Continue doing this until you are left with only one resistor.
- 4 Solve for the source current/voltage (whichever is unknown)
- 5 systematically unwrap the circuit solving as you go along.
First example
Lets go through this example assume we want to know the current through each resistor given that R1=5ohms, R2= 20ohms, R3=20 ohms, and the source is producing 20 volts:
- Step 1 Can not be done because there are no series resistors
- Step 2 Can be done R1 can be combined with R2 to make an effective resistance. R1|R2 is a way of saying R1 in parallel with R2. In this case its is equal to 4 ohms:
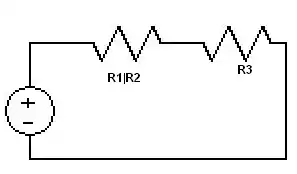
- Step 3 Well were not down to one resistor so we start again we combine the series resistors and get a 24 ohm equivalent resistance.
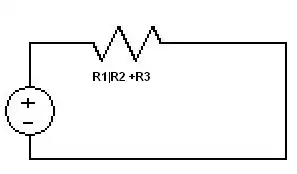
- Step 4 So we know the voltage and the equivalent resistance lets calculate the current. By V=IR we get 5/6 amps.
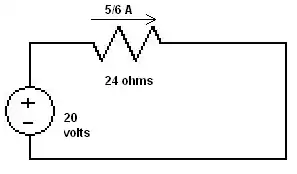
- step 5 Now we start to expand the circuit
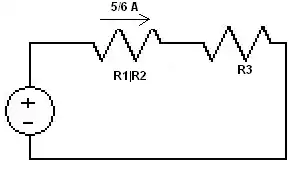
- Since we know the current for the combined resistance and the other resistor is in series we know the current through R3 is equal to 5/6 Amps.
- Step 5 now we unwind the circuit completely and get the final result
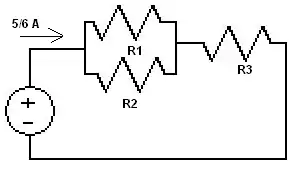
- V=IR, V=(5/6)(4)=20/6. So R1's current is equal to 20/6 divided by 5 which is 2/3 amps. And R2 is 20/6 divided by 20 which is equal to 1/6.
Review
So we see the goal of the technique. We can apply it to any number of circuit problems. Be forewarned this is a hard techniques to master. It is recommend that the student goes through many examples. Remember the basic steps. Combine all the resistors into one resistor. Solve for the current/voltage of that one resistor and then unreduce the circuit solving for each resistor along the way.