Reinforcement learning (RL) is the process of optimizing rewards in a sequential decision making process under uncertainty.
Challenges in RL:
Creating a reinforcement learning algorithm is specifically challenging because of the following items:
- Planning: decisions involve reasoning about not just immediate benefit of a decision but also its longer term benefits
- Temporal credit assignment is hard: it is unclear what actions has lead to rewards
- Exploration: agent only learns from what it has done in the past, so it needs to explore new things to learn more.
Imitation learning reduces RL to supervised learning by learning from experience of others (learning from watching others do something)
Sequential decision making under uncertainty
RL applies to sequential decision making under uncertainty with the objective of optimizing reward.
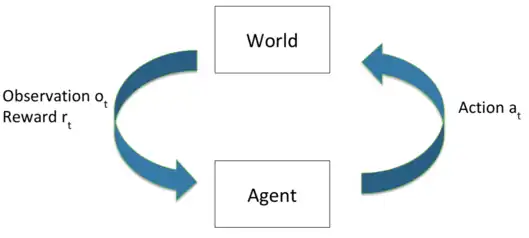
Here we assume the system is Markov:
The actions taken and the future of the system is only dependent on the current state of the system (world/agent) instead of the whole history.
- From another point of view, the state has enough aggregated information from the history of the system to predict the future. Any system can become Markovian if we consider the whole history as the state.
Types of Sequential Decision Processes:
- Bandits: actions have no influence on the next observation. Rewards are immediate.
- Markov Decision Process (MDP) and Partially Observable Markov Decision Process (POMDP): actions influence future observations. In RL algorithm for these types of systems credit assignment and strategic actions may be needed.
Components of RL algorithm
- Model: representation of how world changes in response to agent’s actions.
- Transition / dynamics model is the next state transition probability given the current state and action taken
- The dynamics model might be known (model-based) or unknown (model-free) in the RL algorithm.
- Policy () determines how the agent chooses actions
- Deterministic policy
- Stochastic policy
- The basic problem of reinforcement learning is to find the policy that returns the maximum value.
- Value function: Future rewards from being in a state and/or action when following a particular policy.
- Reward model predicts immediate reward based on state and actions taken:
- The Reward model itself can be deterministic or stochastic, therefore we use an expected value.
- The value function is calculated using the reward model and policy as the expected immediate and future rewards:
- Discount factor weighs immediate vs future rewards
- Reward model predicts immediate reward based on state and actions taken:
Policy Evaluation
Policy evaluation is the process of evaluating the expected reward for a state , given the transition model, policy, and immediate reward function.
We should note that, policy evaluation is related to the optimization problem of finding the optimal policy but does not specifically involve the optimization state.
Policy evaluation builds on top of the following hierarchy of conceptsː
- Markov Chain ː no actions, no rewards
- Markov Rewards Process (MRP)ː Markov Chain + Rewards
- Markov Decision Process (MDP) ː MRP + Actions (read more about MDP here)
- Policy Evaluation : MDP + Policy
State evaluation
In an MRP we can calculate a state value for each state which is called state evaluation. There are a number of methods to calculate for state evaluation:
- Monte Carlo simulation
- Analytic solution
- Dynamic programming / Iterative solution
Furthermore, as explained here, an MDP is reduced to an MRP by choosing a specific policy. Therefore, we can think of the state evaluation process as a policy evaluation process which determines what is the expected value of rewards for each state in the MRP under a certain policy.
Dynamic programing / iterative solution
Policy evaluation is possible using an iterative process, through the following algorithm
- Initialize for all
- For until convergence, for all in
- is exact value of -horizon value of state under policy .
- is an estimate of infinite horizon value of state under policy
In dynamic programming, we bootstrap, or estimate the value of the next state using our current estimate, .
Monte Carlo policy evaluation
- In this method, we simply simulate many trajectories (decision processes), and calculate the average returns.
- The error of calculated reward reduces with , where is the number of trajectories created.
- This method can be used only for episodic decision processes, meaning that the trajectories are finite and terminates after a number of states.
- The evaluation does not require formal derivation of dynamics and rewards models.
- This method does NOT assume states to be Markov.
- Generally a high variance estimator. Reducing the variance can require a lot of data. Therefore, in cases where data is expensive to acquire or the stakes are high, MC may be impractical.
There are different types of Monte Carlo policy evaluation:
- First-visit Monte Carlo
- Every-visit Monte Carlo
- Incremental Monte Carlo
Read more about different types of Monte Carlo Policy Evaluation.
Temporal Difference
- Combination of Monte Carlo and dynamic programing methods
- Model-free
- Bootstraps (builds on top of previous best estimate) and samples
- Can be used for both episodic or infinite-horizon (non-episodic) domains
- Biased estimator of value function
- Immediately updates estimate of V after each
Read more about Temporal Difference Learning.
| Dynamic Programming | Monte Carlo | Temporal Difference | |
|---|---|---|---|
| Model Free? | No | Yes | Yes |
| Non-episodic domains? | Yes | No | Yes |
| Non-Markovian domains? | No | Yes | No |
| Converges to true value? | Yes | Yes | Yes |
| Unbiased Estimate | N/A | Yes (dependes) | No |
| Variance | N/A | High | Low |
On-policy versus Off-policy learning
On-policy learning:
- Direct experience
- Learn to estimate and evaluate a policy from experience obtained from following that policy
Off-policy learning:
- Learn to estimate and evaluate a policy using experience gathered from following a different policy
- In a sense, off-policy learning is like an extrapolation problem that we are trying to make an educated guess based on the available data and predict the situation that has not been experienced before.
Markov Decision Process Control
MDP Control means computing the optimal policy with the maximum value
There is mathematical proof that such optimal value function exists and is unique, however there might be multiple policies that lead to similar optimal value function.
Optimal policy for a MDP in an infinite horizon problem is:
- Deterministic
- Stationary (does not depend on time step)
- Unique? Not necessarily, may have state-actions with identical optimal values
Policy search Algorithms
- Brute force: generally very expensive. Number of deterministic policies
- Policy Iteration: more efficient than brute force
- Value Iteration:
- Idea: maintain optimal value of starting in a state if have a finite number of steps left in the episode
- We iterate to consider longer and longer episodes and eventually converge to the result from policy iteration.
Index
Special:Prefixindex/Reinforcement Learning/
References
- Major source of the content presented on this page and subpages is from Stanford Reinforcement Learning course