Data Types

This is the first of several lessons on the data types used by Python. Computer programs can process instructions that work with many different kinds of data, and the instructions need to be very precise. If you add a word to this sentence, 'add' means something very different from when you add 2 and 3. A computer language has to have a set of rules defining what operations can be applied to different kinds of data, and for this to work, there also has to be a set of rules defining exactly what data can be used with each operation. For example, if you want to calculate grossProfit = salesIncome - costs, a program has to know that these quantities are variables containing numbers rather than just strings of letters. They must have a numerical data type rather than string data type.

If you are not clear about the meaning in computer science of variables and of data types, it may help to brush up on the lesson Introduction_to_Programming/Variables.

>>> type(6)
<class 'int'>
>>> 
>>> type(6.4)
<class 'float'>
>>> 
>>> type('6.4')
<class 'str'>
>>> 
>>> type(b'6.4')
<class 'bytes'>
>>> 
>>> type(['6.4'])
<class 'list'>
>>>

>>> isinstance(6,int)
True
>>> 
>>> isinstance(6,str)
False
>>> 
>>> isinstance('6',str)
True
>>> 
>>> isinstance('6',(int,float,bytes))
False
>>> 
>>> isinstance('6',(int,float,bytes,str))
True
>>> 
>>> isinstance({},dict)
True
>>> 
>>> isinstance({3,4,5},set)
True
>>> 
>>> isinstance(b'',str)
False
>>> 
>>> isinstance(b'',bytes)
True
>>>

Introduction to integers

Python has several data types to represent numbers. This lesson introduces two: integers, and floating point numbers, or 'floats'. We'll discuss floats later in the lesson. An integer, commonly abbreviated to int, is a whole number (positive, negative, or zero). So 7, 0, -11, 2, and 5 are integers. 3.14159, 0.0001, 11.11111, and even 2.0 are not integers, they are floats in Python. To test if this is true, we can use the isinstance built-in function to test if a number is or isn't an integer.

>>> isinstance(7, int)
True
>>> isinstance(0, int)
True
>>> isinstance(-11, int)
True
>>> isinstance(2, int)
True
>>> isinstance(5, int)
True
>>> isinstance(3.14159, int)
False
>>> isinstance(0.0001, int)
False
>>> isinstance(11.11111, int)
False
>>> isinstance(2.0, int)
False

A decimal integer contains one or more digits "0" ... "9". Underscores may be used to improve readability. With one exception described in floats below, leading zeros in a non-zero decimal number are not allowed.

We can perform simple mathematical operations with integers, like addition (+), subtraction (-), multiplication (*), and division (/). Here are some examples using simple math.

>>> 2+2
4
>>> 4-2
2
>>> 6+1
7
>>> 6+7-3
10
>>> 2*2
4
>>> 2*2*2
8
>>> -2
-2
>>> 8/2
4.0
>>> 4*4/2
8.0
>>> 4-4*2
-4
>>> 2-4
-2
>>> 10+10/2
15.0

You should have noticed three things in the above example. First, all mathematical operations follow an order of operations, called precedence; multiplication and division are done first, then addition and subtraction are performed, hence why 10+10/2 didn't result in 10.0. Secondly, when you divide, a float is always the result. Lastly, by putting a minus sign (-) in front of a number, it will become a negative number.

You can do more mathematical operations than the previously demonstrated ones. We can perform a floor division by using two forward slashes (//) to divide and have the result as an integer.

>>> 4 // 2
2
>>> 1 // 8
0
>>> 5 // 5
1
>>> 100 // 5
20
>>> 4 // 3
1

Now, that may save us trouble, but what if we want to get just the remainder of a division? We can perform a modulo operation to get the remainder. To perform a modulo, use a percent sign (%).

>>> 5 % 4
1
>>> 1 % 4
1
>>> 4 % 4
0
>>> 2 % 4
2
>>> 2 % 1
0
>>> 20 % 2
0
>>> 20 % 3
2
>>> -20 % 3
1

The divmod() built-in function returns both quotient and remainder:

>>> divmod(7,3)
(2, 1)
>>> (q,r) = divmod(7,3)
>>> q; r
2
1

You can also find the power of a number by using two asterisk symbols (**).

>>> 4 ** 2
16
>>> 4 ** 4
256
>>> 1 ** 11278923689
1
>>> 2 ** 4
16
>>> 10 ** 2
100
>>> 1024 ** 2
1048576
>>> 10 ** 6
1000000
>>> 25 ** (-1/2)
0.2
>>> 4 * - 3 ** 2
-36
>>> 4 * (- 3) ** 2
36
>>> 8 / 4 ** 2
0.5

The operator of exponentiation (**) has higher precedence than * or / or unary -.

If unsure of precedence, you can always use parentheses to force the desired result:

>>> (4 * (- 3)) ** 2 ; 4 * ((- 3) ** 2)
144
36
>>>

There is no limit for the length of integer literals apart from what can be stored in available memory.

Non-decimal Integers

Almost everyone is familiar with ten based numbers. While base 10 is useful for everyday tasks, it isn't ideal for use in the computer world. Three other numeral systems are commonly used in computer science; binary, octal, and hexadecimal. We'll lightly cover Python's use of these in this section. The binary system is essential as all information is represented in binary form in computer hardware. Octal and hexadecimal are convenient for condensing binary numbers to a form that is more easily read by humans, while (unlike decimal) being simple to translate to or from binary. If you have difficulty with this part of the lesson, it may help to brush up on the lesson Numeral_systems in the course Introduction_to_Computers.

Most people have heard of binary and it is often associated with computers. Actually, modern binary made its way into the world far before electricity was widely in use. The binary system is 2 based, which means that only two numbers are used. Of course, these numbers are 0 and 1. So ${\displaystyle 1+1=10_{2},}$ unlike the decimal's ${\displaystyle 1+1=2_{10}.}$ To use binary numbers in python, prepend 0B or 0b to the number.^[2]

>>> 0B11
3
>>> 0B1 + 0B1
2
>>> 0B11 + 0B1
4
>>> 0B10001 + 0B1
18
>>> 0B10001 - 0B1
16
>>> bin(2345)
'0b100100101001'
>>> 0b_111_0101_0011
1875

The value returned by bin() is a string. The underscore (_) may be used to make numbers more readable.

Note: In computers, a binary digit of information is called a bit.

The octal numeral system is something that really isn't used anymore, since it was superseded by hexadecimal. The octal system made sense decades ago when hardware was expensive, because the 8 based system can fit into three bits perfectly. Though this scheme fits into bits, it does not fit into a standard byte, which is 8 bits. Since the octal numeral system is 8 based, you can only use numbers "0"..."7". To use octal numbers in python, prepend 0o or 0O to the beginning of the number.^[3] You may find it easier to use a lowercase o instead of an uppercase O, since it could be confused as a zero.

>>> 0o3
3
>>> 0o12
10
>>> 0o12 + 0o10
18
>>> 0o12 - 0o03
7
>>> 0o100
64
>>> 0o777
511
>>> 0o777 - 0o111
438
>>> oct(1_234_987)
'0o4554053'
>>> 0o_1234_9876
  File "<stdin>", line 1
    0o_1234_9876
           ^
SyntaxError: invalid token
>>> 0o_1234_0765
2736629

The hexadecimal numeral system is widely used when working with computers, because one hexadecimal digit can fit into a nibble (4 bits). Since a standard byte is 8 bits, two nibbles could perfectly fit into a byte, hence why the octal system is rather obsolete. Hexadecimal has 16 digits, which consist of "0"..."9" and "A"..."F" or "a"..."f". "Letters as numbers?", you may say. Indeed, it may be tricky working with letters as numbers, but once you get comfortable with them, it will be easy to use. To use hexadecimal numbers in python, prepend 0x or 0X to the beginning of the number.^[4] I suggest using a lowercase x, since it is easier to distinguish from the numbers and uppercase letters.

>>> 0xF
15
>>> 0xF0
240
>>> 0xFF - 0xF
240
>>> 0xF + 0xA
25
>>> 0x2 + 0x2
4
>>> 0x12 - 0xA
8
>>> 0xFF / 0xF
17.0
>>> 0xF * 0xF
225
>>> hex(1_234_987)
'0x12d82b'
>>> 0x_12_D82B
1234987

Note: You do not have to use just uppercase letters when working with hexadecimal, you can also use lowercase letters if you find it easier.

This topic has been lightly brushed up on and will probably not be used until later in advanced lessons. If you feel a need to learn this, or you want to be proficient at it, the course Introduction to Computers has a lesson called Numeral systems that deals with these numeral systems with a little more in depth teaching.

>>> bin (0b1010101 & 0b1111)
'0b101'
>>> bin (0b1010101 & 0b111000)
'0b10000'
>>> hex (0xFF00FF & 0xFF00)
'0x0'

0b1010101
0b   1111
      ^ ^

>>> bin (0b1010101 | 0b1110)
'0b1011111'
>>> bin (0b1010101 | 0b1100)
'0b1011101'
>>> hex (0xFF00FF | 0x3F0)
'0xff03ff'

0b1010101
0b   1110
  ^ ^^^^^

>> bin (0b1010101 ^ 0b1110)
'0b1011011'
>>> bin (0b1010101 ^ 0b1100)
'0b1011001'
>>> hex (0xFF00FF ^ 0x3F0)
'0xff030f'

0b1010101
0b   1110
  ^ ^^ ^^

>> bin(0b10101 << 2)
'0b1010100'
>>> bin(0b10101 << 5)
'0b1010100000'
>>> hex(0xFF00FF << 8)
'0xff00ff00'
>>> (0xFF00FF << 8) == (0xFF00FF * 2**8)
True

0b  10101
0b1010100
       ^^

>> bin(0b10101 >> 2)
'0b101'
>>> bin(0b10101 >> 5)
'0b0'
>>> hex(0xFF00FF >> 8)
'0xff00'
>>> (0xFF00FF >> 8) == (0xFF00FF // 2**8)
True

0b10101
0b  101

twoBits = operand & 0x3

>>> hex( ( 0x1234_FEDC << 120 ) | ( 0x_CDE_90AB << 60 ) )
'0x1234fedc00000000cde90ab000000000000000'
>>> hex( ( 0x1234_FEDC << 200 ) ^ ( 0x_CDE_90AB << 207 ) )
'0x67d7cab5c00000000000000000000000000000000000000000000000000'

>>> a = 0b1100101100101 ; bin(~a)
'-0b1100101100110'

>>> a = 0b1100101100101 ; b = a ^ (  (1 << a.bit_length()) - 1  ); bin(b)
'0b11010011010'
>>> c = a + b; bin(c)
'0b1111111111111'   # to test the operation, all bits of c should be set.
>>> (c+1) == ( 1 << (c.bit_length()) )
True                # they are.

from decimal import *
a = 0b11100100011001110001010111    # a is int                                                        
b = bin(a)                          # b is string                                                     
print ('a =', b)

formerPrecision = getcontext().prec
getcontext().prec = a.bit_length()
d = Decimal.logical_invert( Decimal( b[2:] ) )    # d is Decimal object.
getcontext().prec = formerPrecision

print ('d =', d)
e = int(str(d),2)                   # e is int                                                        
print ('e =', bin(e))

( (a + e) == ( ( 1 << a.bit_length() ) - 1 ) ) and print ('successful inversion')

a = 0b11100100011001110001010111
d =      11011100110001110101000
e =    0b11011100110001110101000
successful inversion

Introduction to floats

Although integers are great for many situations, they have a serious limitation, integers are whole numbers. This means that they are not real numbers. A real number is a value that represents a quantity along a continuous line^[5], which means that it can have fractions in decimal forms. 4.5, 1.25, and 0.75 are all real numbers. In computer science, real numbers are represented as floats. To test if a number is float, we can use the isinstance built-in function.

>>> isinstance(4.5, float)
True
>>> isinstance(1.25, float)
True
>>> isinstance(0.75, float)
True
>>> isinstance(3.14159, float)
True
>>> isinstance(2.71828, float)
True
>>> isinstance(1.0, float)
True
>>> isinstance(271828, float)
False
>>> isinstance(0, float)
False
>>> isinstance(0.0, float)
True

As a general rule of thumb, floats have a decimal point and integers do not have a decimal point. So even though 4 and 4.0 are the same number, 4 is an integer while 4.0 is a float.

The basic arithmetic operations used for integers will also work for floats. (Bitwise operators will not work with floats.)

>>> 4.0 + 2.0
6.0
>>> -1.0 + 4.5
3.5
>>> 1.75 - 1.5
0.25
>>> 4.13 - 1.1
3.03
>>> 4.5 // 1.0
4.0
>>> 4.5 / 1.0
4.5
>>> 4.5 % 1.0
0.5
>>> 7.75 * 0.25
1.9375
>>> 0.5 * 0.5
0.25
>>> 1.5 ** 2.0
2.25

Some technical information about 'floats.'

A floating point literal can be either pointfloat or exponentfloat.

A pointfloat contains a decimal point (".") and at least one digit ("0"..."9"), for example:

34.45 ; 34. ; .45 ; 0. ; -.00 ; -33. ;

An exponentfloat contains an exponent which ::= ("e" | "E")["+" | "-"]decinteger.

("e" | "E") means that "e" or "E" is required.

["+" | "-"] means that "+" or "-" is optional.

decinteger means decimal integer.

These are examples of exponents: e9 ; e-0 ; e+1 ; E2 ; E-3 ; E+4 ;

The exponent is interpreted as follows:

${\displaystyle .5e2=.5(10^{2})=50.0;}$ ${\displaystyle -3E1=-3.0(10^{1})=-30.0;}$ ${\displaystyle .003e-5=.003(10^{-5})=3e-08;}$ ${\displaystyle 3e0=3.0(10^{0})=3.0;}$ ${\displaystyle 0090.5e-02=90.5(10^{-2})=0.905;}$ ${\displaystyle 0E0=0.0(10^{0})=0.0;}$

An exponent float can be either:

decinteger exponent, for example: 0e0 ; -3e1 ; 15E-6 ; or

pointfloat exponent, for example: .5E+2 ; -3.00e-5 ; 123_456.75E-5 ;

The separate parts of a floating point number are: 1.2345 = 12345e-4 = ${\displaystyle \underbrace {12345} _{\text{significand}}\times \underbrace {10} _{\text{base}}\!\!\!\!\!\!^{\overbrace {-4} ^{\text{exponent}}}.}$ ^[6]

The significand may be called mantissa or coefficient. The base may be called radix. The exponent may be called characteristic or scale.

Within the floating point literal white space is not permitted. An underscore ("_") may be used to improve readability. Integer and exponent parts are always interpreted using radix 10. Within the context of floating point literals, a "decinteger" may begin with a "0". Numeric literals do not include a sign; a phrase like -1 is actually an expression composed of the unary operator - and the literal 1.

>>> import sys
>>> print ( '\n'.join(str(sys.float_info).split(', ')) )
sys.float_info(max=1.7976931348623157e+308 # maximum representable finite float
max_exp=1024
max_10_exp=308
min=2.2250738585072014e-308 # minimum positive normalized float
min_exp=-1021
min_10_exp=-307
dig=15 # maximum number of decimal digits that can be faithfully represented in a float
mant_dig=53 # float precision: the number of base-radix digits in the significand of a float
epsilon=2.220446049250313e-16
radix=2 # radix of exponent representation
rounds=1)
>>>

>>> sys.float_info.mant_dig
53
>>> 
>>> sys.float_info[7]
53
>>> 
>>> I1 = (1<<53) - 1 ; I1 ; hex(I1) ; I1.bit_length()
9007199254740991
'0x1fffffffffffff'
53
>>> float(I1-1) ; float(I1-1) == I1-1
9007199254740990.0
True
>>> float(I1) ; float(I1) == I1
9007199254740991.0
True
>>> float(I1+1) ; float(I1+1) == I1+1
9007199254740992.0
True
>>> float(I1+2) ; float(I1+2) == I1+2
9007199254740992.0 # Loss of precision occurs here.
False
>>> 
>>> I2 = I1 - 10**11 ; I2 ; hex(I2) ; I2.bit_length() ; float(I2) == I2 ; len(str(I2))
9007099254740991
'0x1fffe8b78917ff'
53
True # I2 can be accurately represented as a float.
16
>>> I3 = I1 + 10**11 ; I3 ; hex(I3) ; I3.bit_length() ; float(I3) == I3 ; len(str(I3))
9007299254740991
'0x2000174876e7ff'
54 # Too many bits.
False # I3 can not be accurately represented as a float.
16
>>>

>>> len(str(I1))
16
>>> 
>>> sys.float_info.dig
15
>>> sys.float_info[6]
15
>>>

>>> sys.float_info.max
1.7976931348623157e+308
>>> 
>>> sys.float_info[0]
1.7976931348623157e+308
>>> 
>>> 1.7976931348623157e+305
1.7976931348623156e+305
>>> 1.7976931348623157e+306
1.7976931348623156e+306
>>> 1.7976931348623157e+307
1.7976931348623158e+307
>>> 1.7976931348623157e+308
1.7976931348623157e+308
>>> 1.7976931348623157e+309
inf
>>>

>>> sys.float_info.min
2.2250738585072014e-308
>>> sys.float_info[3]
2.2250738585072014e-308
>>> 
>>> 2.2250738585072014e-306
2.2250738585072014e-306
>>> 2.2250738585072014e-307
2.2250738585072014e-307
>>> 2.2250738585072014e-308
2.2250738585072014e-308
>>> 2.2250738585072014e-309
2.225073858507203e-309 # Loss of precision.
>>> 2.2250738585072014e-310
2.2250738585072e-310
>>> 2.2250738585072014e-311
2.225073858507e-311
>>>

The Precision of Floats

Before you start calculating with floats you should understand that the precision of floats has limits, due to Python and the architecture of a computer. Some examples of errors due to finite precision are displayed below.

>>> 1.13 - 1.1
0.029999999999999805
>>> 0.001 / 11.11
9.000900090009002e-05
>>> 1 + .0000000000000001
1.0
>>> -5.5 % 3.2
0.9000000000000004
>>> float(1_234_567_890_123_456)
1234567890123456.0
>>> float(12_345_678_901_234_567)
1.2345678901234568e+16

In the first example, 1.13 - 1.1 = 0.03, although Python comes to the conclusion that the real answer is 0.029999999999999805. The fact behind this reasoning is based on how the computer stores memory, so the difference lost a little of its precision. As the minuend increases in size, so does its precision. 2.13 - 1.1 = 1.0299999999999998 and 3.13 - 1.1 = 2.03.

In the second example, 0.001 / 11.11 = 9.000900090009002e-05 where e-05 means ten to the power of negative five. The answer could also be 9.000900090009001e-05 depending on how the quotient is rounded, how long the quotient can be stored on the computer, and the most significant number on the right hand side.

In the third example, the sum of the addends 1 + .0000000000000001 = 1.0 although we know that it really is 1 + .0000000000000001 = 1.0000000000000001. The reason the second addend is left out is because of its insignificance. Although this might not matter for every day situations, it may be important for such uses as rocket science and possibly calculus.

The fourth example gives the correct result if rewritten:

>>> ((-5.5*10 ) % (3.2*10)) / 10.0
0.9

When working with Python floats, we need to be aware that there will probably be a margin of error.

Decimal fixed point and floating point arithmetic for extreme precision

The Python "Decimal" module provides support for fast correctly-rounded decimal floating point arithmetic. The module offers several advantages over the float datatype, including:

• Decimal numbers can be represented exactly.
• The decimal module has a user alterable precision (defaulting to 28 places) which can be as large as needed for a given problem.

The usual start to using decimals is importing the module, viewing the current context with getcontext() and, if necessary, setting new values for precision, rounding, or enabled traps:

>>> from decimal import *

>>> getcontext()
Context(prec=28, rounding=ROUND_HALF_EVEN, Emin=-999999, Emax=999999, capitals=1, clamp=0, flags=[Inexact, FloatOperation, Rounded], traps=[InvalidOperation, DivisionByZero, Overflow])

>>> setcontext(ExtendedContext)
>>> getcontext()
Context(prec=9, rounding=ROUND_HALF_EVEN, Emin=-999999, Emax=999999, capitals=1, clamp=0, flags=[], traps=[])

>>> setcontext(BasicContext)
>>> getcontext()
Context(prec=9, rounding=ROUND_HALF_UP, Emin=-999999, Emax=999999, capitals=1, clamp=0, flags=[], traps=[Clamped, InvalidOperation, DivisionByZero, Overflow, Underflow])

>>> c = getcontext()
>>> c.flags[Inexact] = True
>>> c.flags[FloatOperation] = True
>>> c.flags[Rounded] = True
>>> getcontext()
Context(prec=9, rounding=ROUND_HALF_UP, Emin=-999999, Emax=999999, capitals=1, clamp=0, flags=[Inexact, FloatOperation, Rounded], traps=[Clamped, InvalidOperation, DivisionByZero, Overflow, Underflow])

>>> getcontext().prec = 75    # set desired precision
>>> getcontext()
Context(prec=75, rounding=ROUND_HALF_UP, Emin=-999999, Emax=999999, capitals=1, clamp=0, flags=[Inexact, FloatOperation, Rounded], traps=[Clamped, InvalidOperation, DivisionByZero, Overflow, Underflow])

We are now ready to use the decimal module.

>>> Decimal(3.14)    # Input to decimal() is float.
Decimal('3.140000000000000124344978758017532527446746826171875') # Exact value of float 3.14.

>>> Decimal('3.14')    # Input to decimal() is string.
Decimal('3.14')        # Exact value of 3.14 in decimal floating point arithmetic.

${\displaystyle ({\sqrt {2}})^{2}}$

>>> (2 ** 0.5)**2
2.0000000000000004     # Result of binary floating point operation. We expect 2.

>>> (Decimal('2') ** Decimal('0.5')) ** Decimal('2')
Decimal('1.99999999999999999999999999999999999999999999999999999999999999999999999999')
     # Result of decimal floating point operation with string input. We expect 2.

${\displaystyle (2.12345678^{({\frac {1}{2.345}})})^{2.345}}$

>>> (2.12345678 ** (1/2.345)) ** 2.345
2.1234567800000006      # Result of floating point operation. We expect 2.12345678.

>>> (Decimal('2.12345678') ** (Decimal('1')/Decimal('2.345'))) ** Decimal('2.345')
Decimal('2.12345677999999999999999999999999999999999999999999999999999999999999999999')
     # Result of decimal floating point operation with string input . We expect 2.12345678.

>>> getcontext().rounding=ROUND_UP
>>> (Decimal('2.12345678') ** (Decimal('1')/Decimal('2.345'))) ** Decimal('2.345')
Decimal('2.12345678000000000000000000000000000000000000000000000000000000000000000003')
     # Result of decimal floating point operation with string input . We expect 2.12345678.

Some mathematical functions are also available to Decimal:

>>> getcontext().prec = 30

>>> Decimal(2).sqrt()
Decimal('1.41421356237309504880168872421')

>>> (Decimal(2).sqrt())**2
Decimal('2.00000000000000000000000000001')  # We expect 2.

>>> Decimal(1).exp()
Decimal('2.71828182845904523536028747135')   # Value of 'e', base of natural logs.

>>> Decimal(  Decimal(1).exp()  ).ln()
Decimal('0.999999999999999999999999999999')   # We expect 1.

Lack of precision in the real world

(included for philosophical interest)

>>> a = 899_999_999_999_999.1 ; a - (a - .1)
0.125
>>> 1.13 - 1.1
0.029999999999999805

Simple tests indicate that the error inherent in floating point operations is about ${\displaystyle {\frac {1}{10^{16}}}.}$

This raises the question "How much precision do we need?"

For decades high school students calculated sines and cosines to 4 decimal places by referring to printed look-up tables. Before computers engineers used slide rules to make calculations accurate to about ${\displaystyle {\frac {1}{1000}}}$ for most calculations, and the Brooklyn Bridge is still in regular use.

With accuracy of ${\displaystyle {\frac {1}{10^{16}}}}$ engineers can send a rocket to Pluto and miss by 1cm.

If your calculations produce a result of ${\displaystyle 1.0(10^{-14})}$ and you were expecting ${\displaystyle 0,}$ will you be satisfied with your work? If your calculations were in meters, probably yes. If your calculations were in nanometers (${\displaystyle 10^{-9}}$ of a meter), probably no.

Knowing that lack of precision is inherent in floating point operations, you may have to include possibly substantial amounts of code to make allowances for it.

Extreme Precision

(included for historical interest)

If you must have a result correct to 50 places of decimals, Python's integer math comes to the rescue. Suppose your calculation is:

${\displaystyle 123456.789/4567.87654}$ ${\displaystyle ={\frac {123456.789}{4567.87654}}}$ ${\displaystyle ={\frac {123456.78900}{4567.87654}}}$ ${\displaystyle ={\frac {12345678900}{456787654}}.}$

For 50 significant digits after the decimal point your calculation becomes:

${\displaystyle 123456.789/4567.87654}$ ${\displaystyle ={\frac {12345678900(10^{51})}{456787654(10^{51})}}}$ ${\displaystyle ={\frac {12345678900(10^{51})}{456787654}}/10^{51}.}$

>>> dividend = 12345678900
>>> divisor = 456787654
>>> 
>>> (quotient, remainder) = divmod(dividend*(10**51), divisor) ; quotient;remainder
27027172892899596625262555804540198890751981663672547
231665262
>>> if remainder >= ((divisor + (divisor & 1)) >> 1) : quotient += 1
... 
>>> quotient
27027172892899596625262555804540198890751981663672548
>>>

The correct result ${\displaystyle =27027172892899596625262555804540198890751981663672548(10^{-51}),}$ but note:

>>> quotient*(10**(-51))
27.027172892899596 # Lack of precision.
>>>

Put the decimal point in the correct position within a string to preserve precision:

>>> str(quotient)[0:-51] + '.' + str(quotient)[-51:]
'27.027172892899596625262555804540198890751981663672548'
>>>

Format the result:

>>> s1 = str(quotient)[-51:] ; s1
'027172892899596625262555804540198890751981663672548'
>>> L2 = [ s1[p:p+5] for p in range(0,51,5) ] ; L2
['02717', '28928', '99596', '62526', '25558', '04540', '19889', '07519', '81663', '67254', '8']
>>> decimal = '_'.join(L2) ; decimal
'02717_28928_99596_62526_25558_04540_19889_07519_81663_67254_8'
>>> str(quotient)[0:-51] + '.' + decimal
'27.02717_28928_99596_62526_25558_04540_19889_07519_81663_67254_8'
# The result formatted for clarity and accurate to 50 places of decimals.
>>>

Both strings '27.027172892899596625262555804540198890751981663672548' and

'27.02717_28928_99596_62526_25558_04540_19889_07519_81663_67254_8' are

acceptable as input to Python's Decimal module.

Lack of precision and what to do about it

Lack of precision in floating point operations quickly becomes apparent:

sum = 0
increment = 0.000_000_000_1

for count in range(1,1000) :
    sum += increment
    print ('count= {}, sum = {}'.format(count,sum))
    if sum != count/10_000_000_000 : break

count= 1, sum = 1e-10
count= 2, sum = 2e-10
count= 3, sum = 3e-10
count= 4, sum = 4e-10
count= 5, sum = 5e-10
count= 6, sum = 6e-10
count= 7, sum = 7e-10
count= 8, sum = 7.999999999999999e-10

The problem seems to be that floating point numbers are contained in 53 bits, limiting the number of significant digits in the decimal number displayed to 15 or 16. But this is not really the problem. If the standard limits the number of significant digits displayed to 15 or 16, so be it. The real problem is that underlying calculations are also performed in 53 bits.

>>> (0.000_000_000_1).hex()
'0x1.b7cdfd9d7bdbbp-34'
>>> h1 = '0x1b7cdfd9d7bdbbp-86' # increment with standard precision.
>>> float.fromhex(h1)
1e-10
>>>

>>> x,r = divmod (16**26,10**10) ;x;r
2028240960365167042394
7251286016
>>> x += (r >= (10**10)/2);x
2028240960365167042395
>>> h1 = hex(x)[2:].upper();h1
'6DF37F675EF6EADF5B'
>>> increment = '0x' + h1 + 'p-104' ; increment
'0x6DF37F675EF6EADF5Bp-104' # Current value of increment.
>>> int(increment[:-5],16).bit_length()
71 # Greater precision than standard by 18 bits.
>>> float.fromhex(increment)
1e-10
>>>

>>> from decimal import *
>>> Decimal(x) / Decimal(16**26) 
Decimal('1.0000_0000_0000_0000_0000_01355220626007433600102690740628157139990861423939350061118602752685546875E-10')
>>> # 22 significant digits.

sum = '0x0p0'

for count in range(1,1000) :
    hex_val = sum.partition('p')[0]
    sum = hex( eval(hex_val) + x ) + 'p-104'
    f1 = float.fromhex(sum)
    print (
           'count = {}, sum = {}, sum as float = {}'.format(count, sum, f1)
          )
    if f1 != count/10_000_000_000 : exit(99)

count = 1, sum = 0x6df37f675ef6eadf5bp-104, sum as float = 1e-10
count = 2, sum = 0xdbe6fecebdedd5beb6p-104, sum as float = 2e-10
count = 3, sum = 0x149da7e361ce4c09e11p-104, sum as float = 3e-10
...........................
count = 997, sum = 0x1ac354f2d94d7a0b7dd67p-104, sum as float = 9.97e-08
count = 998, sum = 0x1aca342acfc3697a2bcc2p-104, sum as float = 9.98e-08
count = 999, sum = 0x1ad11362c63958e8d9c1dp-104, sum as float = 9.99e-08

                                      drift
                                       vvv
count = 999, sum = 0x1ad11362c63958e8d9c1dp-104, sum as float = 9.99e-08
                   0x1AD11362C63958E8D9B0Ap-104 most accurate hex representation of sum as float
                     ^^^^^^^^^^^^^^^^^^
                     18 hex digits = 69 bits

                                        drift
                                        vvvvv
count = 99999, sum = 0xa7c53e539be0252c255b85p-104, sum as float = 9.9999e-06
                     0xA7C53E539BE0252C24F026p-104 most accurate hex representation of sum as float
                       ^^^^^^^^^^^^^^^^^
                       17 hex digits = 68 bits

                                               drift
                                              vvvvvvvv
count = 9999999999, sum = 0xffffffff920c8098a1aceb2ca5p-104, sum as float = 0.9999999999
                          0xFFFFFFFF920C8098A1091520A5p-104 most accurate hex representation of sum as float
                            ^^^^^^^^^^^^^^^^^^
                            18 hex digits = 72 bits

                                                       drift
       15 decimal digits                           vvvvvvvvvvvvv
count = 999999999999999, sum = 0x1869fffffffff920c81929f8524a0a5p-104, sum as float = 99999.9999999999
                               0x1869FFFFFFFFF920C8098A1091520A5p-104 most accurate hex representation of sum as float
                                 ^^^^^^^^^^^^^^^^^^
                                 18 hex digits = 69 bits

>>> from decimal import *
>>> getcontext().prec=150
>>> 
>>> top = Decimal(0x1869fffffffff920c81929f8524a0a5); top
Decimal('2028240960365165014154039634832957605')
>>> bottom = Decimal(1<<104); bottom
Decimal('20282409603651670423947251286016')
>>> 
>>> d1 = top/bottom; d1 # Exact value of sum.
Decimal('99999.99999999990000001355220626007432244882064733194557037300120795782210070257178813335485756397247314453125')
>>> len(str(d1))
110
>>> float(d1)
99999.9999999999

>>> 1.13 - 1.1
0.029999999999999805
>>>

from decimal import *

def D(v1) : return Decimal(str(v1))

sum = 0
increment = D(0.000_000_000_1)

for count in range(1,1000) :
    sum += increment
    print ('count = {}, sum = {}'.format(count,sum))
    if sum != count * increment :
        exit (99)

exit (0)

count = 1, sum = 1E-10
count = 2, sum = 2E-10
count = 3, sum = 3E-10
.................
count = 997, sum = 9.97E-8
count = 998, sum = 9.98E-8
count = 999, sum = 9.99E-8

>>> 9.99E-8
9.99e-08
>>> Decimal(str(9.99e-8))
Decimal('9.99E-8')
>>>

sum = 0
increment = 0.000_000_000_1

for count in range(1,1000) :
    sum += increment
    s1 = '{0:.10f}'.format(sum)
    sum = float(s1)
    print ('count= {}, sum = {}'.format(count,sum))
    if sum != count / 10_000_000_000 :	
      	exit (99)

exit (0)

count= 1, sum = 1e-10
count= 2, sum = 2e-10
count= 3, sum = 3e-10
.................
count= 997, sum = 9.97e-08
count= 998, sum = 9.98e-08
count= 999, sum = 9.99e-08

from decimal import *
getcontext().prec = 15

sum = 0
increment = 0.000_000_000_1

for count in range(1,1000) :
    print ( 'count =', ('  '+str(count))[-3:], end='    ' )
    sum += increment
    d1 = Decimal(str(sum))
    print ( 'd1 = sum =', ('                      ' + str(d1))[-21:], end='    ' )
    d1 += 0 # This forces d1 to conform to 15 digits of precision.
    print ( 'd1 =', ('                      ' + str(d1))[-20:], end='    ' )
    sum = float(d1)
    print ('sum =', sum)
    if sum != count / 10_000_000_000 :
        print ('   ', sum, count, increment, count*increment)
        exit (99)

exit (0)

count =   1    d1 = sum =                 1E-10    d1 =                1E-10    sum = 1e-10
count =   2    d1 = sum =                 2E-10    d1 =                2E-10    sum = 2e-10
count =   3    d1 = sum =                 3E-10    d1 =                3E-10    sum = 3e-10
count =   4    d1 = sum =                 4E-10    d1 =                4E-10    sum = 4e-10
count =   5    d1 = sum =                 5E-10    d1 =                5E-10    sum = 5e-10
count =   6    d1 = sum =                 6E-10    d1 =                6E-10    sum = 6e-10
count =   7    d1 = sum =                 7E-10    d1 =                7E-10    sum = 7e-10
count =   8    d1 = sum = 7.999999999999999E-10    d1 = 8.00000000000000E-10    sum = 8e-10
count =   9    d1 = sum =                 9E-10    d1 =                9E-10    sum = 9e-10
count =  10    d1 = sum =                  1E-9    d1 =                 1E-9    sum = 1e-09
count =  11    d1 = sum = 1.1000000000000001E-9    d1 =  1.10000000000000E-9    sum = 1.1e-09
count =  12    d1 = sum =                1.2E-9    d1 =               1.2E-9    sum = 1.2e-09
count =  13    d1 = sum =                1.3E-9    d1 =               1.3E-9    sum = 1.3e-09
count =  14    d1 = sum = 1.4000000000000001E-9    d1 =  1.40000000000000E-9    sum = 1.4e-09
count =  15    d1 = sum =                1.5E-9    d1 =               1.5E-9    sum = 1.5e-09
count =  16    d1 = sum =                1.6E-9    d1 =               1.6E-9    sum = 1.6e-09
..............................
count = 296    d1 = sum =               2.96E-8    d1 =              2.96E-8    sum = 2.96e-08
count = 297    d1 = sum =               2.97E-8    d1 =              2.97E-8    sum = 2.97e-08
count = 298    d1 = sum = 2.9800000000000002E-8    d1 =  2.98000000000000E-8    sum = 2.98e-08
count = 299    d1 = sum = 2.9899999999999996E-8    d1 =  2.99000000000000E-8    sum = 2.99e-08
count = 300    d1 = sum = 3.0000000000000004E-8    d1 =  3.00000000000000E-8    sum = 3e-08
count = 301    d1 = sum =               3.01E-8    d1 =              3.01E-8    sum = 3.01e-08
count = 302    d1 = sum =               3.02E-8    d1 =              3.02E-8    sum = 3.02e-08
..............................
count = 997    d1 = sum =               9.97E-8    d1 =              9.97E-8    sum = 9.97e-08
count = 998    d1 = sum =               9.98E-8    d1 =              9.98E-8    sum = 9.98e-08
count = 999    d1 = sum =  9.989999999999999E-8    d1 =  9.99000000000000E-8    sum = 9.99e-08

A simple way to choose one of two possible values:

>>> L1 = [1,2,0,3,0,5]

Produce list L2, a copy of L1, except that each value 0 in L1 has been replaced by 0xFF:

>>> L2 = []
>>>
>>> for p in L1 :
...     L2 += ([p], [0xFF])[p == 0]
... 
>>> L2
[1, 2, 255, 3, 255, 5]
>>>

Expressions containing multiple booleans

Consider the expression:

A and B or C

Does this mean

(A and B) or C

Does it mean

A and (B or C)

It might be tempting to say that there is no difference, but look closely:

for A in True, False :
    for B in True, False :
        for C in True, False :
            b1 = (A and B) or C
            b2 = A and (B or C)
            if b1 != b2 :
                print (
'''                               
for A = {}, B = {}, C = {}        
(A and B) or C = {}               
A and (B or C) = {}               
'''.format(A, B, C, b1, b2)
                      )

for A = False, B = True, C = True
(A and B) or C = True
A and (B or C) = False

for A = False, B = False, C = True
(A and B) or C = True
A and (B or C) = False

Add another boolean to the expression:

A and B or C and D

and the number of different possibilities is at least 96.

You can see that the complexity of these expressions quickly becomes unmanageable.

The essence of this section: Keep your expressions simple and use parentheses as necessary to ensure that your code is interpreted exactly as you expect.

cmath — Mathematical functions for complex numbers

Introduction

Figure 1: Components of complex number Z. Origin at point ${\displaystyle (0,0)}$. ${\displaystyle Z.real}$ parallel to ${\displaystyle X}$ axis. ${\displaystyle Z.imag}$ parallel to ${\displaystyle Y}$ axis. ${\displaystyle r=abs(Z)}$ ${\displaystyle Z=r(\cos \phi +1j*\sin \phi )=Z.real+1j*Z.imag}$ A Python complex number Z is stored internally using rectangular or Cartesian coordinates. It is completely determined by its real part Z.real and its imaginary part Z.imag. See Figure 1. In Cartesian Geometry of 2 dimensions the real part of complex number Z is parallel to the ${\displaystyle X}$ axis and the imaginary part is parallel to the ${\displaystyle Y}$ axis. The modulus of Z is the line from origin to Z with length r. In scientific notation the number Z is written as ${\displaystyle a+bi}$ where ${\displaystyle i={\sqrt {-1}}.}$ Within Python Z is written as (a + bj). Note: Because the expression 'bj' could be the name of a variable, and to avoid confusion, it might be better to express a complex number within Python as (a + b*1j). The values a,b are the rectangular coordinates of complex number (a + bj). >>> Z = complex(3.6, 2.7) ; Z (3.6+2.7j) >>> Z = 3.6 + 2.7j ; Z (3.6+2.7j) >>> Z = 3.6 + 2.7J ; Z # 'J' upper case. (3.6+2.7j) >>> Z.real ; Z.imag 3.6 2.7 >>> >>> Z.real + 1j*Z.imag (3.6+2.7j) >>> Z.real + 1j*Z.imag == Z True >>> The absolute value of a complex number is the length of the modulus: ${\displaystyle r={\sqrt {Z.real^{2}+Z.imag^{2}}}}$ >>> abs(Z) 4.5 >>> (Z.real**2 + Z.imag**2)**(1/2) 4.5 >>> Some useful constants: >>> import cmath >>> ε = cmath.e ; ε # Greek epsilon, base of natural logarithms. 2.718281828459045 >>> π = cmath.pi ; π # Greek pi. 3.141592653589793 >>> τ = cmath.tau ; τ # Greek tau. 6.283185307179586 >>> τ == 2*π >>> True Addition of complex numbers To add two complex numbers in rectangular format, simply add the real parts, then the imaginary parts: >>> import cmath >>> >>> cn1 = 1+3j ; cn1 (1+3j) >>> cn2 = 2-5j ; cn2 (2-5j) >>> cn1 + cn2 == cn1.real + cn2.real + 1j*(cn1.imag + cn2.imag) True >>>

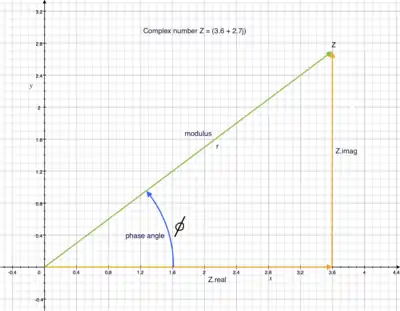
Polar coordinates

Polar coordinates provide an alternative way to represent a complex number. In polar coordinates, a complex number Z is defined by the modulus r and the phase angle φ (phi). The modulus r is abs(Z) as above, while the phase φ is the counterclockwise angle, measured in radians, from the positive x-axis to the line segment that joins the origin to Z.

${\displaystyle \tan \phi ={\frac {Z.imag}{Z.real}}.}$

>>> tan_phi = Z.imag/Z.real ; tan_phi 
0.75
>>> φ = cmath.atan(tan_phi).real ; φ
0.6435011087932844 # φ in radians
>>> φ * (180/π)
36.86989764584402 # φ in degrees.
>>>

Class method cmath.phase(Z) returns the phase:

>>> φ1 = cmath.phase(Z) ; φ1
0.6435011087932844
>>> φ1 == φ
True
>>>

From figure 1:

${\displaystyle \cos \phi ={\frac {Z.real}{r}};\ Z.real=r\cos \phi .}$

${\displaystyle \sin \phi ={\frac {Z.imag}{r}};\ Z.imag=r\sin \phi .}$

If polar coordinates are known:

${\displaystyle Z=r\cos \phi +1j*r\sin \phi =r(\cos \phi +1j*\sin \phi ).}$

>>> Z ; r ; φ
(3.6+2.7j)
4.5
0.6435011087932844
>>> 
>>> cosφ = Z.real / r ; cosφ
0.8
>>> sinφ = Z.imag / r ; sinφ
0.6
>>>
>>> Z1 = r*( cosφ + 1j*sinφ  ) ; Z1
(3.6+2.7j)
>>>

De Moivre's formula

The format containing polar coordinates is useful because:

${\displaystyle Z^{n}=r^{n}(\cos(n\phi )+i\sin(n\phi ))}$

${\displaystyle Z^{2}}$

${\displaystyle Z^{2}=r^{2}(\cos(2\phi )+i\sin(2\phi ))}$ Proof ${\displaystyle Z=r(\cos \phi +i\sin \phi )}$ ${\displaystyle Z^{2}=(r(\cos \phi +i\sin \phi ))^{2}}$ ${\displaystyle Z^{2}=r^{2}(\cos \phi +i\sin \phi )^{2}}$ ${\displaystyle Z^{2}=r^{2}(\cos ^{2}\phi +2i\sin \phi \cos \phi -\sin ^{2}\phi )}$ ${\displaystyle Z^{2}=r^{2}(\cos ^{2}\phi -\sin ^{2}\phi +2i\sin \phi \cos \phi )}$ ${\displaystyle Z^{2}=r^{2}(\cos(2\phi )+i\sin(2\phi ))}$ An example >>> sin2φ = cmath.sin(2*φ).real ; sin2φ 0.96 >>> cos2φ = cmath.cos(2*φ).real ; cos2φ 0.28 >>> Z (3.6+2.7j) >>> Z**2 (5.67+19.44j) >>> r*r*(cos2φ + 1J*sin2φ) (5.67+19.44j) >>> ${\displaystyle Z}$ and ${\displaystyle Z^{2}}$ on polar diagram Figure 2: Z and Z^2. ${\displaystyle abs(Z_{1})=abs(Z_{2})=r_{1}=r_{2}}$. Phase of ${\displaystyle Z_{1}=\phi }$. Phase of ${\displaystyle Z_{2}=180+\phi }$. ${\displaystyle Z_{2}=-Z_{1}}$. ${\displaystyle abs(Z)=r=r_{1}^{2}}$. Phase of ${\displaystyle Z=2\phi }$. ${\displaystyle Z=Z_{1}^{2}=Z_{2}^{2}}$. In Figure 2 ${\displaystyle Z_{1}=3+1j*{\frac {5}{4}}}$. ${\displaystyle Z_{2}=-3+1j*(-{\frac {5}{4}})}$ ${\displaystyle =-3-1j*{\frac {5}{4}}}$ ${\displaystyle =-(3+1j*{\frac {5}{4}})=-Z_{1}.}$ ${\displaystyle r_{1}}$ = length ${\displaystyle OZ_{1}}$ = abs${\displaystyle (Z_{1})=r_{2}}$ = length ${\displaystyle OZ_{2}}$ = abs${\displaystyle (Z_{2})={\frac {13}{4}}.}$ Angle ${\displaystyle \phi }$ is the phase of ${\displaystyle Z_{1}.\ \cos \phi ={\frac {12}{13}}.\ \sin \phi ={\frac {5}{13}}}$. ${\displaystyle Z_{1}=r_{1}*(\cos \phi +1j*\sin \phi )={\frac {13}{4}}*({\frac {12}{13}}+1j*{\frac {5}{13}})=3+1j*{\frac {5}{4}}.}$ ${\displaystyle r}$ = length ${\displaystyle OZ}$ = abs${\displaystyle (Z)=r_{1}^{2}={\frac {169}{16}}.}$ Phase of ${\displaystyle Z=2\phi .}$ Therefore: ${\displaystyle Z=Z_{1}^{2}=Z_{2}^{2}.}$ ${\displaystyle \sin 2\phi =2\sin \phi \cos \phi =2({\frac {5}{13}})({\frac {12}{13}})={\frac {120}{169}}.}$ ${\displaystyle \cos 2\phi =\cos ^{2}\phi -\sin ^{2}\phi =({\frac {12}{13}})({\frac {12}{13}})-({\frac {5}{13}})({\frac {5}{13}})={\frac {144-25}{169}}={\frac {119}{169}}.}$ ${\displaystyle Z=r*(\cos 2\phi +1j*\sin 2\phi )={\frac {169}{16}}({\frac {119}{169}}+1j*{\frac {120}{169}})={\frac {119}{16}}+1j*{\frac {120}{16}}=7{\frac {7}{16}}+1j*7{\frac {1}{2}}.}$ >>> Z1 = 3+1j*(5/4) ; Z1 ; abs(Z1) ; abs(Z1) == 13/4 (3+1.25j) 3.25 True >>> Z = Z1*Z1 ; Z ; Z.real == 7+(7/16) (7.4375+7.5j) True >>>

${\displaystyle {\sqrt {Z}}}$

---

${\displaystyle {\sqrt {Z}}={\sqrt {r}}(\cos(\phi /2)+i\sin(\phi /2))}$

>>> sinφ_2 = cmath.sin(φ/2).real ; sinφ_2
0.31622776601683794
>>> cosφ_2 = cmath.cos(φ/2).real ; cosφ_2
0.9486832980505138
>>> Z
(3.6+2.7j)
>>> cmath.sqrt(Z)
(2.0124611797498106+0.670820393249937j)
>>> (r**0.5)*(cosφ_2 + 1J*sinφ_2)
(2.0124611797498106+0.6708203932499369j)
>>>

${\displaystyle {\sqrt {1}}}$

${\displaystyle \cos(0)+1j*\sin(0)=1+1j*0=1}$ ${\displaystyle {\sqrt {1}}={\sqrt {\cos(0)+1j*\sin(0)}}}$ ${\displaystyle =\cos(0/2)+1j*\sin(0/2)}$ ${\displaystyle =\cos(0)+1j*\sin(0)=1}$ Trigonometric functions are cyclical: ${\displaystyle \cos(360)+1j*\sin(360)=1+1j*0=1}$ ${\displaystyle {\sqrt {1}}={\sqrt {\cos(360)+1j*\sin(360)}}}$ ${\displaystyle =\cos(360/2)+1j*\sin(360/2)}$ ${\displaystyle =\cos(180)+1j*\sin(180)=-1+1j*0=-1}$ The two square roots of 1 are 1 and -1. >>> 1**2 ; (-1)**2 1 1 >>>

${\displaystyle {\sqrt {-1}}}$

${\displaystyle \cos(180)+1j*\sin(180)=-1+1j*0=-1}$ ${\displaystyle {\sqrt {-1}}={\sqrt {\cos(180)+1j*\sin(180)}}}$ ${\displaystyle =\cos(180/2)+1j*\sin(180/2)}$ ${\displaystyle =\cos(90)+1j*\sin(90)=0+1j*1=1j}$ Trigonometric functions are cyclical: ${\displaystyle \cos(180+360)+1j*\sin(180+360)=-1+1j*0=-1}$ ${\displaystyle {\sqrt {-1}}={\sqrt {\cos(180+360)+1j*\sin(180+360)}}}$ ${\displaystyle =\cos(90+180)+1j*\sin(90+180)}$ ${\displaystyle =\cos(270)+1j*\sin(270)=0+1j*(-1)=-1j}$ The two square roots of -1 are 1j and -1j. >>> (1j)**2 ; (-1j)**2 (-1+0j) (-1+0j) >>>

Cube roots of 1 simplified

${\displaystyle \cos(0)+1j*\sin(0)=1+1j*0=1}$ ${\displaystyle {\sqrt[{3}]{1}}=(\cos(0)+1j*\sin(0))^{(1/3)}}$ ${\displaystyle =\cos(0/3)+1j*\sin(0/3)}$ ${\displaystyle =\cos(0)+1j*\sin(0)=1}$ Trigonometric functions are cyclical: ${\displaystyle \cos(360)+1j*\sin(360)=1+1j*0=1}$ ${\displaystyle {\sqrt[{3}]{1}}=(\cos(360)+1j*\sin(360))^{(1/3)}}$ ${\displaystyle =\cos(360/3)+1j*\sin(360/3)}$ ${\displaystyle =\cos(120)+1j*\sin(120)=-\cos(60)+1j*\sin(60)}$ ${\displaystyle =-{\frac {1}{2}}+1j{\frac {\sqrt {3}}{2}}={\frac {-1+1j*{\sqrt {3}}}{2}}}$ Proof: ${\displaystyle r_{2}=-1(\cos(60)-1J*\sin(60))=-1(\cos(-60)+1J*\sin(-60)).}$ ${\displaystyle r_{2}^{3}=(-1)^{3}(\cos(-180)+1J*\sin(-180))=-1(-1+1J*0)=1.}$ ${\displaystyle \cos(720)+1j*\sin(720)=1+1j*0=1}$ ${\displaystyle {\sqrt[{3}]{1}}=(\cos(720)+1j*\sin(720))^{(1/3)}}$ ${\displaystyle =\cos(720/3)+1j*\sin(720/3)}$ ${\displaystyle =\cos(240)+1j*\sin(240)=-\cos(60)-1j*\sin(60)}$ ${\displaystyle =-{\frac {1}{2}}-1j{\frac {\sqrt {3}}{2}}={\frac {-1-1j*{\sqrt {3}}}{2}}}$ Proof: ${\displaystyle r_{3}=-1(\cos(60)+1J*\sin(60))}$. ${\displaystyle r_{3}^{3}=(-1)^{3}(\cos(180)+1J*\sin(180))=-1(-1+1J*0)=1.}$ The three cube roots of 1 are : ${\displaystyle 1,-\cos 60^{\circ }\pm 1j*\sin 60^{\circ }}$ or ${\displaystyle 1,\ {\frac {-1+1j*{\sqrt {3}}}{2}},\ {\frac {-1-1j*{\sqrt {3}}}{2}}.}$ >>> r1 = 1 ; v1 = r1**3 ; v1 1 >>> r2 = ( -1 + 1j * (3**0.5)) / 2 ; v2 = r2**3 ; v2 (0.9999999999999998+1.1102230246251565e-16j) >>> r3 = ( -1 - 1j * (3**0.5)) / 2 ; v3 = r3**3 ; v3 (0.9999999999999998-1.1102230246251565e-16j) >>> >>> [ cmath.isclose(v,1,abs_tol=1e-15) for v in (v1,v2,v3) ] [True, True, True] >>>

Multiplication of complex numbers

To multiply two complex numbers in polar format, multiply the moduli and add the phases. >>> cn1 = 3+4j ; cn1 (3+4j) >>> r1,φ1 = cmath.polar(cn1) ; r1 ; φ1 5.0 0.9272952180016122 # radians >>> >>> cn2 = -4+3j ; cn2 (-4+3j) >>> r2,φ2 = cmath.polar(cn2) ; r2 ; φ2 5.0 2.498091544796509 # radians >>> >>> v1 = cn1*cn2 ; v1 (-24-7j) >>> v2 = 25*( cmath.cos(φ1 + φ2) + 1j*cmath.sin(φ1 + φ2) ) ; v2 # r1 * r2 = 25 (-24-7.000000000000002j) >>> >>> cmath.isclose(v1, v2, abs_tol=1e-15) True >>> Proof ${\displaystyle (\cos A+1j*\sin A)*(\cos B+1j*\sin B)}$ ${\displaystyle =\cos A\cos B+1j*\cos A\sin B+1j*\sin A\cos B+j^{2}\sin A\sin B}$ ${\displaystyle =\cos A\cos B-\sin A\sin B+1j*(\cos A\sin B+\sin A\cos B)}$ ${\displaystyle =\cos(A+B)+1j*\sin(A+B)}$