Decision trees are a class of non-parametric algorithms that are used supervised learning problems: Classification and Regression.
There are many variations to decision tree approach:
- Classification and Regression Tree (CART)
- Bootstrap aggregation
- Random forest
- Boosting aggregation
Decision tree algorithms are discriminative models.
Classification and Regression Tree (CART)
Classification and Regression Tree (CART) analysis is the use of decision trees for both classification (discrete output) and regression (continuous) problems.
- CART analysis is the simplest form of decision tree algorithms.
- Setup:
- There is an input training data set, , that is used to grow (train) the tree.
- Here, is the input value for the i-th sample which could be -dimensional.
- Also is the output value for that sample and is a discrete (classification) or continuous (regression) value.
- Main idea:
- The decision tree is a binary trees that output a value () from each leaf of tree.
- The output value from each leaf is chosen such that it minimize an defined error metric within that leaf.
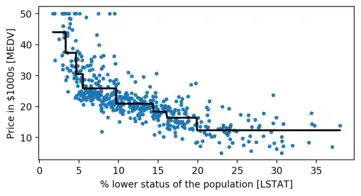
Regression trees
- The decision tree outputs () a continuous value.
- The error that is minimized in each leaf is defined as
- The output value from each leaf is the average of data points in that leaf
 Classification tree on iris dataset
Classification tree on iris dataset

Classification trees
- The decision tree outputs () a discrete value.
- The error metric that is minimized in each leaf is defined as the misclassification ratio
- The output value from each leaf is the majority vote of data points in that leaf.
Advantages and Limitations
Advantages
Amongst other machine learning methods, decision trees have various advantages:
- Simple to understand and interpret. People are able to understand decision tree models after a brief explanation. Trees can also be displayed graphically in a way that is easy for non-experts to interpret.
- Able to handle both numerical and categorical data. Other techniques are usually specialized in analyzing datasets that have only one type of variable. (For example, relation rules can be used only with nominal variables while neural networks can be used only with numerical variables or categoricals converted to 0-1 values.)
- Requires little data preparation. Other techniques often require data normalization. Since trees can handle qualitative predictors, there is no need to create intermediate variables.
- Uses a white box or open-box model and easy to debug. If a given situation is observable in a model the explanation for the condition is easily explained by boolean logic. By contrast, in a black box model, the explanation for the results is typically difficult to understand, for example with an artificial neural network.
- Possible to validate a model using statistical tests. That makes it possible to account for the reliability of the model.
- Makes no assumptions of the training data or prediction residuals; since decision tree is a non-statistical approach it has no assumption on the statistical properties of the training data e.g., no distributional, independence, or constant variance assumptions
- Performs well with large datasets. The cost of using the tree (i.e., predicting data) is logarithmic in the number of data points used to train the tree.
- Mirrors human decision-making more closely than other approaches. This could be useful when modeling human decisions/behavior.
- Robust against co-linearity, particularly boosting
- Built-in feature selection. Additional irrelevant feature will be less used so that they can be removed on subsequent runs. The hierarchy of attributes in a decision tree reflects the importance of attributes. It means that the features on top are the most informative.
Limitations
- Trees can be sensitive to small changes in the training data.
- Local optimal decisions: The problem of learning an optimal decision tree is known to be NP-complete under several aspects of optimality and even for simple concepts. Consequently, practical decision-tree learning algorithms are based on heuristics such as the greedy algorithm where locally optimal decision are made at each node. To reduce the greedy effect of local optimality, some methods such as the dual information distance (DID) tree were proposed.
- It is possible to overfit the the decision tree. This type of tree does not generalize well. Mechanisms such as pruning are necessary to avoid this problem.
- Decision tree learners create biased trees if some classes dominate. It is therefore recommended to balance the dataset prior to fitting with the decision tree.
Complexity
In general, the run time cost to construct a balanced binary tree is and query time is .
How to create (grow) a decision tree?
Note that finding the global optimal tree is an NP-hard problem. Here we show a greedy algorithm to find a local optimum solution.
Regression decision tree
Do the following step recursively for each branch of the tree (subregion of the training data) until the stop criteria is met
- Choose dimension and decision boundary in that dimension such that it minimizes the following quantity
- Stop criteria could be one of the following
- One one data point is left in each region
- Only consider splits resulting in regions with points left in the region
After creating the tree, we use some pruning strategy which results in better performance for the tree. Using other algorithms such as random forest, bootstrap aggregation, or random subspaces could also improve performance
- Generally, a simple CART tree suffers from high variance on the training data.
Classification decision tree
To be completed