Given:

${\displaystyle \varphi =a~x_{1}^{2}+b~x_{1}~x_{2}+c~x_{2}^{2}}$

Find the problem which fits this solution.

${\displaystyle \sigma _{11}=\varphi _{,22}=2c~;~~\sigma _{22}=\varphi _{,11}=2a~;~~\sigma _{12}=-\varphi _{,12}=-b}$

This is a homogeneous stress field. An infinite number of problems can satisfy these conditions.

Given:

${\displaystyle \varphi =a~x_{1}^{3}+b~x_{1}^{2}~x_{2}+c~x_{1}~x_{2}^{2}+d~x_{2}^{3}}$

Find the problem which fits this solution.

${\displaystyle \sigma _{11}=2cx_{1}+6dx_{2}~;~~\sigma _{22}=6ax_{1}+2bx_{2}~;~~\sigma _{12}=-2bx_{1}-2cx_{2}}$

An infinite set of problems can have this stress field as a solution.

If ${\displaystyle a=b=c=0}$, then

${\displaystyle \sigma _{11}=6dx_{2}~;~~\sigma _{22}=0~;~~\sigma _{12}=0}$

which corresponds to a plane stress beam under pure bending.

Pure bending of an elastic beam

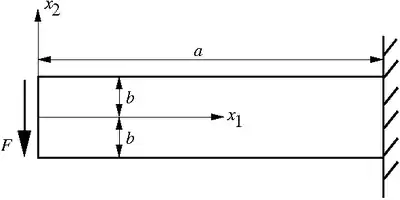
Consider a cantilevered beam that is fixed at one end and has a vertical force F applied at the free end.

Bending of a cantilevered beam

The boundary conditions on the beam are

${\displaystyle {\begin{matrix}\sigma _{12}&=0~;~~x_{2}=\pm b\\\sigma _{22}&=0~;~~x_{2}=\pm b\\\sigma _{11}&=0~;~~x_{1}=0\\\int _{-b}^{b}\sigma _{12}dx_{2}&=F~;~~x_{1}=0\\\mathbf {u} &=\mathbf {0} ~;~~x_{1}=a\end{matrix}}}$

We will use Maple to solve the problem.

First, assume a polynomial Airy stress function that has a high enough order. In this case a fourth order polynomial will suffice
phi:=C1*x^2+C2*x*y+C3*y^2+C4*x^3+C5*x^2*y+C6*x*y^2+ C7*y^3+C8*x^4+C9*x^3*y+C10*x^2*y^2+C11*x*y^3+C12*y^4;

${\displaystyle {\begin{aligned}\phi &:={\mathit {C1}}\,x^{2}+{\mathit {C2}}\,x\,y+{\mathit {C3}}\,y^{2}+{\mathit {C4}}\,x^{3}+{\mathit {C5}}\,x^{2}\,y+{\mathit {C6}}\,x\,y^{2}+{\mathit {C7}}\,y^{3}\\&+{\mathit {C8}}\,x^{4}+{\mathit {C9}}\,x^{3}\,y+{\mathit {C10}}\,x^{2}\,y^{2}+{\mathit {C11}}\,x\,y^{3}+{\mathit {C12}}\,y^{4}\end{aligned}}}$

Take the derivatives of the stress function to obtain the expressions for the stresses.
sxx1:= diff(phi,y,y); syy1:= diff(phi,x,x); sxy1:= -diff(phi,x,y);

${\displaystyle {\begin{aligned}{\mathit {sxx1}}&:=2\,{\mathit {C3}}+2\,{\mathit {C6}}\,x+6\,{\mathit {C7}}\,y+2\,{\mathit {C10}}\,x^{2}+6\,{\mathit {C11}}\,x\,y+12\,{\mathit {C12}}\,y^{2}\\{\mathit {syy1}}&:=2\,{\mathit {C1}}+6\,{\mathit {C4}}\,x+2\,{\mathit {C5}}\,y+12\,{\mathit {C8}}\,x^{2}+6\,{\mathit {C9}}\,x\,y+2\,{\mathit {C10}}\,y^{2}\\{\mathit {sxy1}}&:=-{\mathit {C2}}-2\,{\mathit {C5}}\,x-2\,{\mathit {C6}}\,y-3\,{\mathit {C9}}\,x^{2}-4\,{\mathit {C10}}\,x\,y-3\,{\mathit {C11}}\,y^{2}\end{aligned}}}$

Next, use the command unapply(...,x,y) to configure the stresses as functions of x,y so that we can find the value at various points, e.g., ${\displaystyle y=b}$.
sxx2:=unapply(sxx1,x,y): syy2:=unapply(syy1,x,y): sxy2:=unapply(sxy1,x,y):

We now find the tractions on ${\displaystyle y=b}$ as
t1:=syy2(x,b); t2:=sxy2(x,b);

${\displaystyle {\begin{aligned}{\mathit {t1}}&:=2\,{\mathit {C1}}+6\,{\mathit {C4}}\,x+2\,{\mathit {C5}}\,b+12\,{\mathit {C8}}\,x^{2}+6\,{\mathit {C9}}\,x\,b+2\,{\mathit {C10}}\,b^{2}\\{\mathit {t2}}&:=-{\mathit {C2}}-2\,{\mathit {C5}}\,x-2\,{\mathit {C6}}\,b-3\,{\mathit {C9}}\,x^{2}-4\,{\mathit {C10}}\,x\,b-3\,{\mathit {C11}}\,b^{2}\end{aligned}}}$

and on ${\displaystyle y=-b}$
t3:=syy2(x,-b); t4:=sxy2(x,-b);

${\displaystyle {\begin{aligned}{\mathit {t3}}&:=2\,{\mathit {C1}}+6\,{\mathit {C4}}\,x-2\,{\mathit {C5}}\,b+12\,{\mathit {C8}}\,x^{2}-6\,{\mathit {C9}}\,x\,b+2\,{\mathit {C10}}\,b^{2}\\{\mathit {t4}}&:=-{\mathit {C2}}-2\,{\mathit {C5}}\,x+2\,{\mathit {C6}}\,b-3\,{\mathit {C9}}\,x^{2}+4\,{\mathit {C10}}\,x\,b-3\,{\mathit {C11}}\,b^{2}\end{aligned}}}$

On ${\displaystyle x=0}$, we have
t5:=sxx2(0,y); t6:=sxy2(0,y);

${\displaystyle {\begin{aligned}{\mathit {t5}}&:=2\,{\mathit {C3}}+6\,{\mathit {C7}}\,y+12\,{\mathit {C12}}\,y^{2}\\{\mathit {t6}}&:=-{\mathit {C2}}-2\,{\mathit {C6}}\,y-3\,{\mathit {C11}}\,y^{2}\end{aligned}}}$

The stress function is order 4, so the stresses are order 2 in x and y. The tractions on ${\displaystyle y=+b}$ or ${\displaystyle -b}$ might therefore be polynomials in ${\displaystyle x}$ of order 2.

We calculate the coefficients of each power of x in these expressions as
s1:=coeff(t1,x,2); s2:=coeff(t1,x,1); s3:=coeff(t1,x,0); s4:=coeff(t2,x,2); s5:=coeff(t2,x,1); s6:=coeff(t2,x,0); s7:=coeff(t3,x,2); s8:=coeff(t3,x,1); s9:=coeff(t3,x,0); s10:=coeff(t4,x,2); s11:=coeff(t4,x,1); s12:=coeff(t4,x,0);

${\displaystyle {\begin{aligned}{\mathit {s1}}&:=12\,{\mathit {C8}}\\{\mathit {s2}}&:=6\,{\mathit {C4}}+6\,{\mathit {C9}}\,b\\{\mathit {s3}}&:=2\,{\mathit {C1}}+2\,{\mathit {C5}}\,b+2\,{\mathit {C10}}\,b^{2}\\{\mathit {s4}}&:=-3\,{\mathit {C9}}\\{\mathit {s5}}&:=-2\,{\mathit {C5}}-4\,{\mathit {C10}}\,b\\{\mathit {s6}}&:=-{\mathit {C2}}-2\,{\mathit {C6}}\,b-3\,{\mathit {C11}}\,b^{2}\\{\mathit {s7}}&:=12\,{\mathit {C8}}\\{\mathit {s8}}&:=6\,{\mathit {C4}}-6\,{\mathit {C9}}\,b\\{\mathit {s9}}&:=2\,{\mathit {C1}}-2\,{\mathit {C5}}\,b+2\,{\mathit {C10}}\,b^{2}\\{\mathit {s10}}&:=-3\,{\mathit {C9}}\\{\mathit {s11}}&:=-2\,{\mathit {C5}}+4\,{\mathit {C10}}\,b\\{\mathit {s12}}&:=-{\mathit {C2}}+2\,{\mathit {C6}}\,b-3\,{\mathit {C11}}\,b^{2}\end{aligned}}}$

The biharmonic equation is 4th order, so applying it to a 4th order polynomial generates a constant. And this constant must be equal to zero.
biharm:=diff(phi,x$4)+diff(phi,y$4)+2*diff(phi,x,x,y,y);

${\displaystyle {\mathit {biharm}}:=24\,{\mathit {C8}}+24\,{\mathit {C12}}+8\,{\mathit {C10}}}$

We also calculate the three force resultants on x=0 by integrating over y:
Fx:=int(t5, y=-b..b): Fy:=int(t6, y=-b..b): M:=int(t5*y, y=-b..b):

We now solve for the constants so as to satisfy (i) the strong boundary conditions, (ii) the biharmonic equation and (iii) the weak boundary conditions.
solution:=solve({s1=0,s2=0,s3=0,s4=0,s5=0,s6=0,s7=0, s8=0,s9=0,s10=0,s11=0,s12=0,biharm=0,Fx=0,M=0,Fy=F}, {C1,C2,C3,C4,C5,C6,C7,C8,C9,C10,C11,C12});

${\displaystyle {\begin{aligned}{\text{solution}}&:=\{{\mathit {C7}}=0,\,{\mathit {C8}}=0,\,{\mathit {C9}}=0,\,{\mathit {C4}}=0,\,{\mathit {C10}}=0,\,{\mathit {C5}}=0,\\&{\mathit {C12}}=0,\,{\mathit {C1}}=0,\,{\mathit {C3}}=0,\,{\mathit {C6}}=0,\,{\mathit {C11}}={\cfrac {F}{4\,b^{3}}},\,{\mathit {C2}}=-{\cfrac {3\,F}{4\,b}}\}\end{aligned}}}$

Notice that there are more equations than there are constants. Some of the equations are not linearly independent. However, Maple can handle this if there is a solution.

Substitute the solution into the original stress function and calculate the final stresses.
phi:=subs(solution,phi); sxx3:=diff(phi,y,y); syy3:=diff(phi,x,x); sxy3:=-diff(phi,x,y);

${\displaystyle \phi$ :=-{\cfrac {3\,F\,x\,y}{4\,b}}+{\cfrac {F\,x\,y^{3}}{4\,b^{3}}}}

and

${\displaystyle {\begin{aligned}{\mathit {sxx3}}&:={\cfrac {3\,F\,x\,y}{2\,b^{3}}}\\{\mathit {syy3}}&:=0\\{\mathit {sxy3}}&:={\cfrac {3\,F}{4\,b}}-{\cfrac {3\,F\,y^{2}}{4\,b^{3}}}\end{aligned}}}$

Stress distribution in an elastic cantilevered beam.

Displacement Boundary Condition

The displacement potential function must satisfy the relations ${\displaystyle \psi _{,12}=\nabla ^{2}{\varphi }}$ and ${\displaystyle \nabla ^{2}{\psi }=0}$.

In this problem,

${\displaystyle \varphi =-{\cfrac {3Fx_{1}x_{2}}{4b}}+{\cfrac {Fx_{1}x_{2}^{3}}{4b^{3}}}}$

Therefore,

${\displaystyle \psi _{,12}={\cfrac {6Fx_{1}x_{2}}{4b^{3}}}}$

Integrating,

${\displaystyle \psi ={\cfrac {3F}{8}}x_{1}^{2}x_{2}^{2}+f(x_{1})+g(x_{2})}$

${\displaystyle \nabla ^{2}{\psi }=0}$ only if

${\displaystyle {\cfrac {3F}{4}}(x_{1}^{2}+x_{2}^{2})+f^{''}(x_{1})+g^{''}(x_{2})=0}$

which means that

${\displaystyle f^{''}(x_{1})=-{\cfrac {3F}{4}}x_{1}^{2}+G~;~~g^{''}(x_{2})=-{\cfrac {3F}{4}}x_{2}^{2}-G~;~~}$

These can be integrated to find ${\displaystyle f(x_{1})}$ and ${\displaystyle g(x_{2})}$ in terms of ${\displaystyle x_{1}}$, ${\displaystyle x_{2}}$ and constants. The constants can be determined from the displacement BCs applied so as to fix rigid body motion.

The displacements are given by

${\displaystyle {\begin{matrix}u_{1}&=-{\cfrac {P}{2EI}}(a^{2}-x_{1}^{2})x_{2}-{\cfrac {P(2+\nu )}{6EI}}x_{2}^{3}+{\cfrac {P(1+\nu )b^{2}}{8EI}}x_{2}\\u_{2}&=-{\cfrac {Pa^{3}}{6EI}}\left[2-{\cfrac {3x_{1}}{a}}\left(1-{\cfrac {\nu x_{2}^{2}}{a^{2}}}\right)+{\cfrac {x_{1}^{3}}{a^{3}}}+{\cfrac {3b^{2}(1+\nu )}{4a^{2}}}\left(1-{\cfrac {x_{1}}{a}}\right)\right]\end{matrix}}}$

where ${\displaystyle I=(1/12)w(2b)^{3}\,}$, and ${\displaystyle w}$ = thickness of the beam.

• Since ${\displaystyle u_{1}}$ is no a linear function of ${\displaystyle x_{2}}$, plane sections do not remain plane.
• ${\displaystyle u_{1}(a,x_{2})\neq 0}$ and ${\displaystyle u_{2}(a,x_{2})\neq 0}$, but St. Venant's principle can be applied.
• The deflection of the neutral axis (${\displaystyle x_{2}=0}$) is

${\displaystyle u_{2}(x_{1},0)=-{\cfrac {Pa^{3}}{6EI}}\left[2-{\cfrac {3x_{1}}{a}}+{\cfrac {x_{1}^{3}}{a^{3}}}+{\cfrac {3b^{2}(1+\nu )}{4a^{2}}}\left(1-{\cfrac {x_{1}}{a}}\right)\right]}$

If ${\displaystyle b/a\rightarrow 0}$, this prediction approaches beam theory.

• The maximum deflection is

${\displaystyle u_{2}(0,0)=-{\cfrac {Pa^{3}}{3EI}}-{\cfrac {Pa^{3}}{6EI}}{\cfrac {3b^{2}(1+\nu )}{4a^{2}}}}$