Derivative of a function at a number
Notation
We denote the derivative of a function at a number as .
Definition
The derivative of a function at a number a is given by the following limit (if it exists):
An analagous equation can be defined by letting . Then , which shows that when approaches , approaches :
Interpretations
As the slope of a tangent line
Given a function , the derivative can be understood as the slope of the tangent line to at :
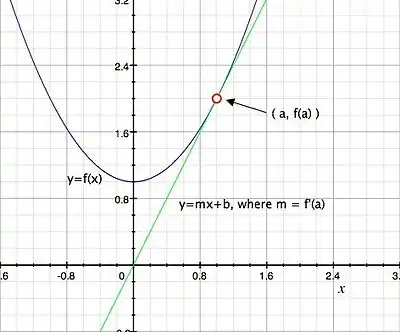
As a rate of change
The derivative of a function at a number can be understood as the instantaneous rate of change of when .
At a tangent to one point of a curve
Vocabulary
The point A(a ; f(a)) is the point in contact of the tangent and Cf.
Definition
If f is differentiable in a, then the curve C admits at a point A which has for coordinates (a ; f(a)), a tangent : it is the straight line passing by A and of direction coefficient f'(a). An equation of that tangent is written: y = f'(a)*(x-a)+f(a)
| Go to the School of Mathematics |