A convolution between two signals, and , is an operation defined as follows:
The process of convolution is very useful in the time domain analysis of systems, because we can fully describe a system by its impulse response. Let's consider the following system which operates on an input as , having characterized its impulse response by :
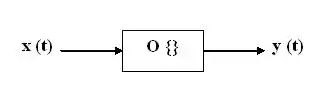
Put into other words, the output of a system in an instant can be written as a linear combination of past and future instants of the input and its impulse response:
Discrete Convolution
In discrete time there is no continuous time but finite samples .
So the integral can be rewritten as a sum
To understand the convolution of finite length signals better, let's look at an example with the signals and .
[ 1] * [6 9] = ?
[ 6 12 18 0] // [1 2 3] * 6
[ 0 9 18 27] // [1 2 3] * 9
-------------
[ 6 21 36 27] // sum of the above
Note that the length of the output signal has the length where is the length of and the length of .