Strain Measures in three dimensions
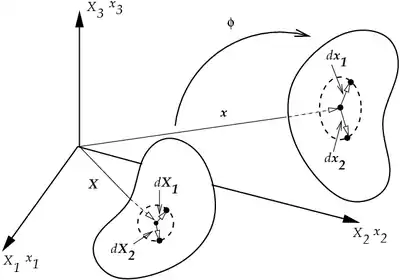 The motion of a body |
Initial orthonormal basis:
Deformed orthonormal basis:
We assume that these coincide.
Motion
Deformation Gradient
Effect of :
Dyadic notation:
Index notation:
The determinant of the deformation gradient is usually denoted by and is a measure of the change in volume, i.e.,
Push Forward and Pull Back
Forward Map:
Forward deformation gradient:
Dyadic notation:
Effect of deformation gradient:
Push Forward operation:
- = material vector.
- = spatial vector.
Inverse map:
Inverse deformation gradient:
Dyadic notation:
Effect of inverse deformation gradient:
Pull Back operation:
- = material vector.
- = spatial vector.
Example
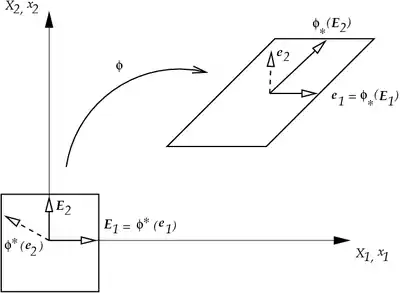 Push forward and pull back |
Motion:
Deformation Gradient:
Inverse Deformation Gradient:
Push Forward:
Pull Back:
Cauchy-Green Deformation Tensors
Right Cauchy-Green Deformation Tensor
Recall:
Therefore,
Using index notation:
Right Cauchy-Green tensor:
Left Cauchy-Green Deformation Tensor
Recall:
Therefore,
Using index notation:
Left Cauchy-Green (Finger) tensor:
Strain Measures
Green (Lagrangian) Strain
Green strain tensor:
Index notation:
Almansi (Eulerian) Strain
Almansi strain tensor:
Index notation:
Push Forward and Pull Back
Recall:
Now,
Therefore,
Push Forward:
Pull Back:
Some useful results
Derivative of J with respect to the deformation gradient
We often need to compute the derivative of with respect the the deformation gradient . From tensor calculus we have, for any second order tensor
Therefore,
|
|
Derivative of J with respect to the right Cauchy-Green deformation tensor
The derivative of J with respect to the right Cauchy-Green deformation tensor () is also often encountered in continuum mechanics.
To calculate the derivative of with respect to , we recall that (for any second order tensor )
Also,
From the symmetry of we have
Therefore, involving the arbitrariness of , we have
Hence,
Also recall that
Therefore,
|
|
In index notation,
|
|
Derivative of the inverse of the right Cauchy-Green tensor
Another result that is often useful is that for the derivative of the inverse of the right Cauchy-Green tensor ().
Recall that, for a second order tensor ,
In index notation
or,
Using this formula and noting that since is a symmetric second order tensor, the derivative of its inverse is a symmetric fourth order tensor we have
|
|