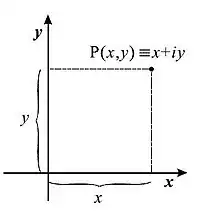
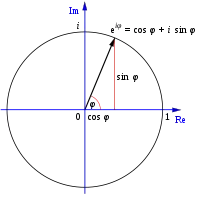
Complex Numbers

Complex Number

The set of complex numbers is denoted $\mathbb {C}$ . A complex number $z\in \mathbb {C}$ can be written in Cartesian coordinates as

z=a+ib

where $a,b\in \mathbb {R}$ . $a$ is called the 'real part' of $z$ and $b$ is called the 'imaginary part' of $z$ . These can also be written in a trigonometric polar form, as

z=r(\cos(\vartheta )+i\sin(\vartheta ))

where $r\in \mathbb {R}$ is the 'magnitude' of $z$ and $\vartheta \in [-\pi ,\pi )$ is called the 'argument' of $z$ . These two forms are related by the equations

{\begin{aligned}r&={\sqrt {a^{2}+b^{2}}}\\\vartheta &=\arctan \left({\frac {b}{a}}\right).\end{aligned}}

The trigonometric polar form can also be written as

z=re^{i\vartheta }

by using Euler's Identity

e^{i\vartheta }=\cos(\vartheta )+i\sin(\vartheta ).

Coordination

  $z=x+yi$  in Cartesian form,
  $z=|z|(\cos \vartheta +i\sin \theta )$  in trigonometric polar form,
  $z=|z|e^{i\vartheta }\,$  in polar exponential form.

Complex conjugate Number

A complex number $z^{*}\in \mathbb {C}$ is a complex conjugate of a number $z\in \mathbb {C}$ if and only if

z\cdot z^{*}=1.

If a complex number $z$ is written as $z=a+ib$ , then the conjugate is

z^{*}=a-ib.

Equivalently in polar form if $z=re^{i\vartheta }$ then

z^{*}=re^{-i\vartheta }=r(\cos(\vartheta )-i\sin(\vartheta )).

Mathematical Operations

Operation on 2 different complex numbers

Addition	$(a+ib)+(c+id)=(a+c)+i(b+d)$
Subtraction	$(a+ib)-(c+id)=(a-c)+i(b-d)$
Multiplication	$(a+ib)\cdot (c+id)=(ac-bd)+i(ad+bc)$
Division	${\frac {(a+ib)}{(c+id)}}={\frac {(a+ib)}{(c+id)}}{\frac {(c-id)}{(c-id)}}={\frac {(ac+bd)+i(bc-ad)}{c^{2}+d^{2}}}$

Operation on complex numbers and its conjugate

Addition	$(a+ib)+(a-ib)=2a$
Subtraction	$(a+ib)-(a-ib)=2ib$
Multiplication	$(a+ib)(a-ib)=a^{2}+iab-iab+b^{2}=a^{2}+b^{2}$
Division	${\frac {(a+ib)}{(a-ib)}}={\frac {(a+ib)}{(a-ib)}}{\frac {(a+ib)}{(a+ib)}}={\frac {(a+ib)^{2}}{a^{2}+b^{2}}}$

In Polar form

Operation on complex number and its conjugate

z\cdot z^{*}=|z|\angle e^{i\vartheta }\cdot |z|\angle e^{-i\vartheta }=|z|^{2}e^{i(\vartheta -\vartheta )}=|z|^{2}e^{0}=|z|^{2}

{\frac {z}{z^{*}}}={\frac {|z|e^{i\vartheta }}{|z|e^{-i\vartheta }}}=e^{2i\vartheta }

Operation on 2 different complex numbers

z_{1}\cdot z_{2}=|z_{1}|e^{i\vartheta _{1}}\cdot |z_{1}|e^{i\vartheta _{2}}=|z_{1}z_{2}|e^{i(\vartheta _{1}+\vartheta _{2})}

{\frac {z_{1}}{z_{2}}}={\frac {|z_{1}|e^{i\vartheta _{1}}}{|z_{2}|e^{i\vartheta _{2}}}}=\left|{\frac {z_{1}}{z_{2}}}\right|e^{i(\vartheta _{1}-\vartheta _{2})}

Complex power

A careful analysis of the power series for the exponential, sine, and cosine functions reveals the marvelous

Euler formula

 $e^{i\theta }=\cos \theta +i\sin \theta \,$

of which there is the famous case (for θ = π):

e^{i\pi }=-1\,

More generally,

 $x+yi=r(\cos \theta +i\sin \theta )=re^{i\theta }\,$

de Moivre's formula

 $(\cos(x)+i\sin(x))^{n}=\cos(nx)+i\sin(nx)$

for any real $x$ and integer $n$ . This result is known as .

Transcendental functions

The higher mathematical functions (often called "transcendental functions"), like exponential, log, sine, cosine, etc., can be defined in terms of power series (Taylor series). They can be extended to handle complex arguments in a completely natural way, so these functions are defined over the complex plane. They are in fact "complex analytic functions". Many standard functions can be extended to the complex numbers, and may well be analytic (the most notable exception is the logarithm). Since the power series coefficients of the common functions are real, they work naturally with conjugates. For example:

\sin({\overline {z}})={\overline {\sin(z)}}\,

\log({\overline {z}})={\overline {\log(z)}}\,

Summary

Complex number

  $z=x+yi$  . In Rectangular plane 
  $z=z\angle \theta$  . In Polar plane
  $z=z(\cos \theta +i\sin \theta )$  . In trigonometry
  $z=ze^{j\theta }\,$  . In Complex plane

Complex conjugate number

  $z^{*}=x-yi$  . In Rectangular plane 
  $z^{*}=z\angle -\theta$  . In Polar plane 
  $z^{*}=z^{*}(\cos \theta -i\sin \theta )$  . In trigonometry angle
  $z^{*}=z^{*}e^{j\theta }\,$  . In Complex plane

Complex Number

Complex conjugate Number

Mathematical Operations

Operation on 2 different complex numbers

Operation on complex numbers and its conjugate

In Polar form

Complex power

Euler formula

de Moivre's formula

Transcendental functions

Summary

References

See Also