A polynomial function is a function compromising of more than one non-negative integer powers of x. An example of this would be:
- 3x2 + 4x - 5
- 8x4 + 12x3 - 2x2 + 5x - 5
- 6x7 - 5
A degree is determined by whichever power is the highest. Example: The first polynomial, 3x2 + 4x - 5, has as the highest degree since it is the highest power in the polynomial. The leading coefficient is the coefficient with the highest degree (not value). Example: The second polynomial, 8x4 + 12x3 - 2x2 + 5x - 5, has "8" as its leading coefficient since it is the number that is associated with the highest degree, being "4".
A quadratic is a polynomial with the highest degree being . A cubic polynomial, or simply "cubic", is a polynomial with the highest degree being .
Graphs
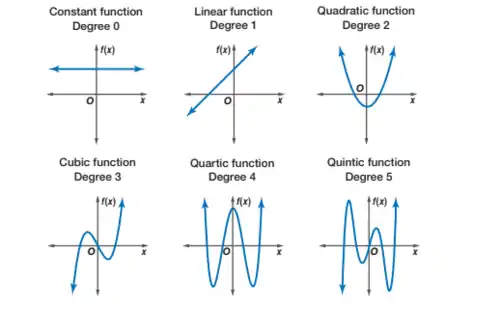
Watch closely how the degrees are related to the zeroes of the function (the intersection of the x-axis by the graph). They seem to correlate each other (be the exact same as each other).
Observe the end behavior. Which direction does x or f(x) lead to? Positive or negative infinity (take note that the functions go infinity and never stop at a certain point)? This is represented by x→+∞ and x→−∞ (x-approaching positive infinity and x-approaching negative identity, respectively). The degree and leading coefficient of a polynomial function determine the end behavior of the polynomial function graph. See Varsity Tutors - End Behavior of a Function (examples) for more examples of end behavior of functions.
- If the x-axis was intersected twice or thrice, it has two/three real zeroes.
- If the x-axis was not intersected at all, its roots are imaginary.
- If the function was tangent to the x-axis, this means it is a double root, which represents two zeroes at the same number (x-axis point).
A function is even if both sides of the function go the same direction, while a function is odd if both sides of the function go in opposite directions.
You determine the number of degrees and the total number of solutions for a function by counting the turns of the graph and adding one to it.
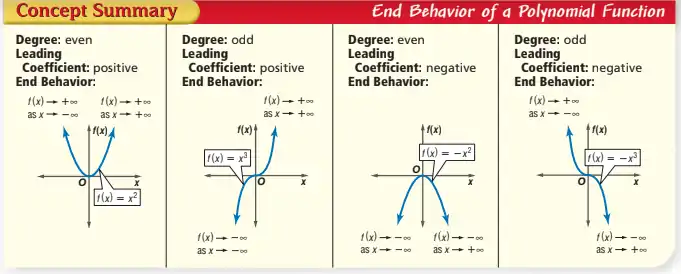
Maximum and Minimum Points
The maximum point is the highest point (in terms of the y-coordinate) on the function. The minimum point is the opposite. These are often referred to as "turning points". These are the points on which you count the turns.