Optimization in elementary geometry: case study

Here is a seemingly simple problem, belonging probably to recreational mathematics. I heard it somewhere long ago.

Problem. Partite a square into five convex polygons of equal diameter so as to minimize this diameter.

Clarification. The diameter of a convex polygon is the maximal length of all its edges and diagonals.

Do you know any algorithmic approach for solving such problems? I do not. If you do, please let us know.

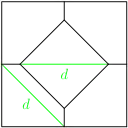
The partition that usually comes to mind first is shown on Fig. 1. It is admissible (that is, meets the requirements: five convex polygons of equal diameter) and symmetric (as symmetric as the square). But it appears to be nonoptimal. Here the diameters (shown in green on Fig. 1) are equal to ${\displaystyle d_{1}={\sqrt {0.5}}\approx 0.71}$ (of the side of the given square, assumed to be 1 from now), which follows easily from Pythagorean theorem.

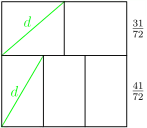
A better partition is shown on Fig. 2. Here the diameters are equal to ${\displaystyle \textstyle d_{2}={\frac {\sqrt {2257}}{72}}\approx 0.66;}$ we observe that ${\displaystyle d_{2}}$ is less than ${\displaystyle d_{1},}$ which shows that the first partition is nonoptimal.

You may wonder, how did I find this better partition. This was a process involving, besides logic, such components as geometric intuition, trials and errors, insight, good luck. Let me explain it as far as I can.

My stating point was the observation that the fifth, the central part on Fig. 1 is effectively useless. It is formally needed just because we need five parts. Yes, but the partition of the square into four half-sized squares gives the same diameter! I asked myself: why so? how to benefit from the fifth part? I answered to myself: because the fifth part is isolated from the boundary of the given square; I should arrange five parts adjacent to the boundary.

This way I came to the configuration of Fig. 2, but with a parameter ${\displaystyle y}$ instead of the number ${\displaystyle 41/72,}$ not knowing yet, is this configuration better or worse than the first one. By Pythagorean theorem (again), the diameter in the lower three parts is ${\displaystyle \textstyle {\sqrt {{\frac {1}{9}}+y^{2}}},}$ but ${\displaystyle \textstyle {\sqrt {{\frac {1}{4}}+(1-y)^{2}}}}$ in the upper two parts. They must be equal, whence ${\displaystyle \textstyle {\frac {1}{9}}+y^{2}={\frac {1}{4}}+(1-y)^{2};\;}$ ${\displaystyle \textstyle y^{2}-(1-y)^{2}={\frac {1}{4}}-{\frac {1}{9}};\;}$ ${\displaystyle \textstyle 2y=1+{\frac {1}{4}}-{\frac {1}{9}}={\frac {41}{36}};\;}$ and finally ${\displaystyle \textstyle y={\frac {41}{72}}.}$ Accordingly, ${\displaystyle \textstyle d_{2}^{2}={\frac {1}{9}}+y^{2}={\frac {1}{9}}+{\frac {41^{2}}{72^{2}}}={\frac {1}{9}}+{\frac {1}{9}}\cdot {\frac {41^{2}}{24^{2}}}={\frac {1}{9}}(1+{\frac {41^{2}}{24^{2}}})={\frac {1}{9}}({\frac {24^{2}+41^{2}}{24^{2}}})={\frac {1}{9}}{\frac {2257}{24^{2}}};\;}$ ${\displaystyle \textstyle d_{2}={\frac {1}{3}}\cdot {\frac {\sqrt {2257}}{24}}={\frac {\sqrt {2257}}{72}}\approx 0.66}$ as stated.

So... I still do not know, whether the second configuration is optimal, or not. Have you any idea? If you have, please let us know.

User:By doing