When, in 1797, Venturi had announced that one found, in the manuscripts of Leonardo da Vinci, one or other of the essential laws of modern Mechanics, the surprise of many geometers was obliged to be mixed with a regret. On certain points, the great painter had preceded Galileo by a century. If he had been able, during his lifetime, to publish the Treatise on Movement and the Treatise on Weight that he was preparing; if at least, in default of this publication, the fragments that he left could have been known immediately after his death, what impulsion would the study of Mechanics have received! Galileo, Simon Stevin, Descartes, would have, at the beginning of their works, found this science more advanced by a stage on the road of progress; by an effort equal to the one that they have given, they would have been able to lead it for a greater distance than they had actually taken it; all the development of the positive sciences from it would have been hastened. Thus the oblivion, for ever deplorable, in which, during some centuries, the thoughts of Leonardo da Vinci touching the principles of Mechanics have remained, has imposed to the march of the human spirit an irremediable delay.
This delay did not happen. Since the middle of the XVIth century, the most essential ideas of Leonardo da Vinci touching Statics and Dynamics were known by those who interested themselves in these sciences; in the pillage in which the manuscript notes of the great artist were handed over, the geometers and the mechanicists made an ample booty; without revealing to the public the source of their riches, they retailed them in their writings; happy larceny, which increased, it is true, in an unmerited fashion the glory of certain authors, but who, at least, exhumed and put back in circulation a portion of the treasures amassed by Leonardo!
Among these who possessed themselves, in order to order them, comment on them and develop them, of the thoughts of Leonardo da Vinci, it is fitting to cite in the first line Jérôme Cardan; he was not alone, some others preceded him or imitated him; it is thus, not to give but one example, that we recover the influence of Leonardo in the writings of Jean-Baptiste Benedetti; but Cardan was of the first to publish the most essential results that the great painter had obtained in meditating on Mechanics; his great notoriety, the ample diffusion of his works, made them to be known everywhere; it is by the writings of Cardan that the ideas of Leonardo arrived to Galileo, to Kepler, to Simon Stevin and that they exerted, on the development of Mechanics, a powerful and beneficent influence.
The opinion that we have just expressed has, for the history of Mechanics, some grave consequences (1). It shows us in the writings of Leonardo and of Cardan the conduit from where the peripatetician Mechanics, after having a long while slept in the basin where the scholastic commentators shut it up, has poured itself out in modern science to fertilize it. If this opinion is right, it is called for to throw a great day for the evolution which has shed of its archaic shell the seeds contained in the science of the School and with them has effected to produce the science of the XVIIth century. It is important therefore to stay it from solid arguments.
That the manuscripts of Leonardo da Vinci had been, in the middle of the XVIth century, the object of a veritable pillage, this is a fact unfortunately too certain; one is familiar with the negligence with which they acquitted themselves of their mission, those who had the guard of this precious deposit: "Not only have the works drafted by the great painter perished, said Libri (2), but we have lost also most of the books where he wrote his notes. After his death, all his manuscripts, his designs and his instruments became the property of François Melzi, his student, to whom he had bequeathed them. Melzi, who was not but a devotee, placed this precious heritage in his house in Vaprio near Milan; his descendants did not hold any account of them and a certain Lelio Gavardi, parent of Alde Manuce the younger, and tutor of this family, having remarked that this beautiful collection was being allowed to waste, stole thirteen of these manuscripts, and carried them to Tuscany in order to sell them to the grand duke François I; but this prince had just died, and they were deposited in Pisa at the house of Alde, who showed them to his friend Mazenta. This latter one disapproved strongly of the conduct of Gavardi who, ashamed of his bad action, charged him to bring back to Milan and to restore these manuscripts to the Melzi. Horace, then head of this family, ignoring the value of these thirteen volumes, made a gift of them to Mazenta and said to him that a lot of other designs and manuscripts of Leonardo had been forgotten in a corner of his house in Vaprio. Many devotees obtained afterwards the designs, the instruments, the anatomical preparations, at length all that remained of the practice of Leonardo. Pompée Leoni, sculptor in the service of Philippe II, was of the better allotted..."
Thus, in the treasure amassed by the genius of Leonardo, each ransacked according to his fancy and took what pleased him. The treatises were retained by those who took interest in them, or circulated from hand to hand until they were mislaid. We know by Pacioli (3) that Leonardo had completely finished the editing of his Treatise of Painting; Vasari, in his Lives of the Best Painters, Sculptors and Architects (4), recounts having seen this manuscript treatise in the hands of a Milanian painter, who was wanting to print it in Rome. Leonardo had equally finished the editing of a Treatise on Perspective; Cellini, in the work that he published in Florence, in 1568, on the same subject, says several times that he had in hand this Treatise, that he had lent it to Sarlio, and that the latter had drawn from it what there is of the better in his work.
Of these Treatises of Leonardo, some copies, some extracts more or less faithful, were circulating in Italy and outside of Italy; this is after one such copy, sent by Del Pozzo, that Du Fresne, in 1651, caused to imprint in Paris as the Treatise on Painting. One other copy, more complete, conserved at the Vatican Library, permitted by Manzi to give from it, in 1817, an edition less impoverished.
The painters and the designers knew what profit they would be able to draw from the pillage of the manuscipts of Leonardo; the mechanicists were scarcely less well-informed. In the XVIth century, the machines that they had invented were still in use and kept the name of their author (5). These therefore who interested themselves in the theory of equilibrium and of movement were assured to discover a rich booty of new ideas in the collection that the carelessness of the Melzi delivered to depredations.
At Milan, not far from the house of Vaprio who kept so badly this treasure, lived Jérôme Cardan. Jérôme Cardan is one of these universal spirits that Italy produced, marvelously fecund, from the XVth and from the XVIth century; as Leonardo da Vinci before him, as Galileo after him, he seems apt to comprehend all the sciences and to perfect them all. Doctor of great renown, he devoted himself to algebra and caused to effect the theory of equations some considerable progress. He unites, elsewhere, from prodigious inconsistencies, ideas most audacious and superstitions most puerile. Astrology and the divination of dreams occupy him scarcely less than sound physics and rigorous arithmetic.
His respect for the intellectual richesse of others does not go as far as scruple; he does not blush to weight the baggage of his own discoveries by slipping into it some borrowings made from the science of his contemporaries. One example makes proof of it.
Excited by a question of Antoine Fiore, who took after Ferro of Bologne a method for resolving an equation of the third degree, Tartaglia (6) succeeded in resolving all the equations of this order. His discovery, which he hid carefully, to the end of being able to support sure challenges to his rivals—as a duelist keeps a secret thrust—finished nevertheless by being sweated out. Cardan interested himself in it vigorously. Several times, he solicited and contrived to solicit Tartaglia so that he would communicate to him his method. After having endured many refusals, he obtained a piece of verse in which was explained the means to have a root of all equations of the third degree. In order to obtain this information, he had not hesitated to engage his Christian faith and his word as a gentleman that he would never publish the method of which he was asking of Tartaglia the revelation: "Io vi giuro, he wrote him, ad sacra Dei evangelia, et da real gentil'huomo, non solamente di non publicar giammai tale vostra inventione, se me le insignate. . . ." When he was familiar with the solution so ardently desired, he was eager to publish it in his Ars Magna. Tartaglia complained vigorously of the perjury thanks to which his discovery appeared for the first time in the book of others. "He had reason to complain," said Libri, "for posterity has been obstinate to call from the name Cardan the formula which gives the resolution of equations of the third degree." Cardan, however, had recognized the priority of Tartaglia, thus that of his predecessors Scipion Ferro and Antoine Fiore; of Ferro, Tartaglia did not cite even the name, when in his turn he published his solution. The geometers of the XVIth century had an irritable self-respect when one possessed oneself of their proper discoveries, but a large conscience when they borrowed the discoveries of others.
One would imagine with difficulty that Cardan, so avid to be familiar with the windfall of Tartaglia and so prompt, despite his swearing, to adorn his book of Algebra from it, would not have suffered from the curiosity to be familiar with the thoughts of Leonardo da Vinci on Mechanics and Physics and, having been familiar with them, that he would have resisted the temptation of gleaning from them some or others in order to nourish his own meditations. He did not resist it.
In 1551, Cardan published his twenty-one books On Subtlety (7); a second Latin edition (8) of this work, more complete than the the first, appeared as early as 1554 and, in 1556, was translated into French by Richard le Blanc (9); the French or Latin editions of this work succeeded themselves, numerously, during the second half of the XVIth century (10). To this writing, Cardan joined later his Opus novum de proportionibus (11). All the Mechanics contained in these two works carry, still recognizable, the mark of Leonardo.
Between the Statics of Leonardo and the Statics of Cardan, the concordance is incessant; the second is scarcely but an edition better ordered than the first; but it would be idle for us to dwell on this concordance; the reading of the pages which will follow will make it clearly apparent.
As one will see it in Chapter IV, Leonardo da Vinci and Cardan do not agree less than exactly in what touches the impossibility of perpetual motion.
The harmony between them is perfect on the subject of the principles of Dynamics; and it is so much the more significant that their opinions on diverse questions of Dynamics have a form very peculiar that one scarcely finds in the works of their predecessors or their contemporaries.
We hope that it will be given to us, someday, to retrace the origins of Dynamics, as we retrace today the origins of Statics; this will be the place to analyze in detail the Dynamics of Leonardo da Vinci and of Cardan and the influence that it has had on the development of rational Mechanics. We will see then the doctrine of the Milanese doctor to be inspired down to the least details from the sparse thoughts in the manuscripts of the great painter.
The borrowings made by Cardan from the Physics of Leonardo da Vinci are less numerous, not that one cannot recognize a few: thus Cardan, wanting to explain how one can light a fire at the focus of a concave mirror, says (12): "The fire which is engendered from mirrors hollowed or raised in clear rotundity, appertains to co-progression. And the reason of the co-progression is not obscure, for if you distribute ten deniers to ten men, each one will have a denier; if you distribute them to five, each one will have two deniers. If therefore the heat which is dispersed in a great space is assembled, all that which was from heat in this great space will be in a small one; however this great assembling of heat contained in this small space will produce great effects, which will merit to be called great, and for this the fire will be engendered."—Now Leonardo da Vinci had written (13): "Of the quality of the heat produced by the rays of the sun in the mirror. The heat of the sun which will be found at the surface of the concave mirror will be divided among the pyramidal rays converging to a single point; so many times this point goes into the surface, so many times it will be hotter than the heat which is found on the mirror; also so many times ab or, if you wish, cd (14), goes into the mirror, so many times its heat will be more powerful than that of the mirror." He had again written elsewhere this passage (15): "One same quality is as much more powerful as it occupies a smaller place. This is understood for heat, for percussion, for weight, for force and for a lot of other things.
- "We will speak first of the heat of the sun, which impresses itself in the concave mirror and is reflected from it in pyramidal figure, a pyramid which acquires proportionally as much more power as it compresses itself more. This is to say if the pyramid hits the object with half of its length, the pyramid compresses half of its density in the lower part; and if the pyramid hits at 99 hundredths of its length, it will compress itself from 99 hundredths of its base and grows from 99 hundredths of the heat that the base receives from the said heat from the sun or from the fire."
One can bring together equally, although in a manner less intimate, the response given by Cardan (16) to this question: "How are the colors of the celestial arc called Iris caused?" with what Leonardo has written of the rainbow (17).
But, in a crowd of occasions, Cardan does not hesitate to turn aside from his illustrious predecessor; on the subject of tides, of the scintillation of the stars, of the suspension of the clouds in the atmosphere, he adopts some solutions distinct from the ones that Leonardo had proposed; his theory of heat, of fire, and of the elastic force of gas is of its own; and this is possibly the most remarkable part of the books On Subtlety.
Cardan was therefore not a vulgar plagiarist; he knew to extract the juice from the thoughts sown by Leonardo, to assimilate them, to transform them and to nourish in his turn the science of the XVIth century from ideas which, for want of his happy indiscretion, were hidden, unused and unknown, shrouded in the house of Melzi.
Even in the domain of Mechanics, where his borrowings from Leonardo have been particularly numerous, he has known, as we are going to see, to set the imprint of his originality next to the seal of genius that had impressed his predecessor.
Cardan disdained not at all to exercise his talent for geometry in some demonstrations constructed in the manner of Archimedes and to fill certain lacunae that the illustrious Syracusian had left gaping. Thus Archimedes had always neglected the weight of the lever or of the balance beam to which he was suspending the loads from which he would study the equilibrium; Cardan had in view determining the mechanical properties of a horizontal, homogenous balance beam suspended by any whatsoever of its points. This is the object of the article entitled, in the De Subtilitate (18), "Staterae ratio" and that his translator Richard Le Blanc designates in these terms: "The manner of the lever vulgarly called in Paris a sleigh, of what customarily the weavers make use, in Latin Statera (19)."
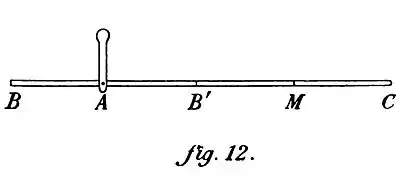
Cardan made his analysis repose on two propositions taken for axioms. He admits, in the first place, that one segment AB' (fig. 12), equal to the small arm AB of the beam and taken on the great arm, makes equilibrium with small arm AB; he admits, in the second place, that the rest B'C of the great arm weighs as if it were an load equal in weight hung in the center M of B'C: "If the balance [beam] is deemed without weight and, from the part which is the difference of the longitudes from the mechanical play, an equal load be extended through all of the member, it will have heaviness equal to the same load hung at the point distant from the hand of the balance through the middle of the whole member."
These principles give easily the solution of the problem posed. This problem, Cardan treats anew in the Opus Novum (20) and he attains to this proposition: The weights (moments) of the two arms AB, AC of the beam are between them as the squares of the lengths of these two arms.
Cardan, elsewhere, does not dissimulate his satisfaction in having obtained one such solution: "Hoc est", says he (21), "quod Archimedes reliquit intactum, cum esset maxime necessarium et ostendit magis abstrusa sed, pace illius dixerim, minus utilia."
This solution was possibly not so arduous to obtain that it were meriting this song of triumph; nevertheless, it had, on the reasonings of the successors of Cardan, an undoubtable influence. Abandoning the requirements that Archimedes had placed at the base of his reasonings on the equilibrium of the lever, Simon Stevin on one part, Galileo on another part, will bring back the study of the lever to the consideration of a homogenous weighted bar, suspended in its middle, and that by means of the same axioms that Cardan has proposed. Now Galileo was familiar if not with the Opus novum, with at least the De Subtilitate, that he cites frequently in his first works; it would be arduous to allow that Simon Stevin had not taken cognizance of any of the multiple editions of this work; as for the Opus novum, the Flemish geometer cites it and critiques it.
These demonstrations of Statics, conceived in the manner of Archimedes, do not at all form the most important part of the considerations that Cardan dedicates to the equilibrium of weights; after another manner of gravity by their significance are the developments that he gives to the axiom of Aristotle; enriching and transforming this axiom by the aid of the thoughts
that Leonardo da Vinci has sown in his manuscripts, he makes from them the Principle of virtual velocities, such as Galileo will employ it, such as it will remain until Descartes.
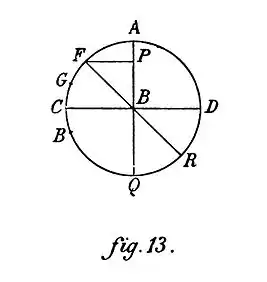
Let us begin from a quotation, from which we will analyze, afterwards, the rich content. Here is how, in the first book of the De Subtilitate, Cardan expresses himself (22), translated by Richard Le Blanc: "Of the balance and of its measure. After these things, it is necessary to see some loads which are placed on the balance. Therefore let a balance be, from which the stem be hung at A (fig. 13), and the lancet where are joined the sides of the balance be CD.... I say that the loads set at C will be more powerful than if the balance were being set in some other place, for instance than if it were being set at F. Now, in order that we know that C is heavier in such a situation than in F, it is necessary that it be moved in equal time through greater space towards the center [of the world]. For we see that the heaviest things, all things being equal, are carried more lightly [rapidly] to the center. Now that this comes to more from the load and from the balance rather placed at C than at F, I show by two reasons.
"The first reason is that if in any time the load is moved from C to E, and that the arc CE be equal to FG, that it would descend from F to G more slowly than from C to E, and thus it will be more light at F than at C.... It is evident from the balances and from those which lift the burdens, that so much the more the burden is far from the lancet, so much the more it is heavy; now the load at C is far from the lancet by the quantity of the line BC and at F, by the quantity of the line FP.... Therefore this reason is general, that so much the more the loads are far from the boundary, or line of the descent by the line right or oblique, that is to say by the angle, so much the more are heavy.... And thus the intention of the load is to be carried in right lines to the center; but for that which it is prevented by ligature, it is moved as it is able."
Thus when a weight descends following the vertical, the power of motion of this weight is, as Aristotle would want it, measured by the velocity with which it falls; but, by the agency of the mechanism which carries it, by the nature of the links [liaisons], according to the word employed by Cardan and reprised by modern Mechanics, it can happen that the weight does not move itself according to the vertical; then, in order to estimate its power of motion, it will be necessary to take account not of the total velocity of the weight, but solely of the vertical component of this velocity or, in other terms, of the velocity of fall.
If therefore one suspends a given weight in some point from a solid moving around a horizontal axis, the motive power of this weight will be so much the greater as the point of suspension lowers itself more rapidly by the effect of a given rotation, imparted to the support; hence, the motive power will be so much the greater as the point of suspension is more distant from the vertical plane containing the axis.
It is for us today very easy to achieve this analysis and, from the premises posed, to draw forth the proportionality between the motive power of the suspended weight and the distance from the point of suspension to the vertical plane containing the axis; It suffices for us to carry ourselves back to the definition of the velocity of fall, the proportion of an infinitesimal fall to its infinitely small duration; we see thus that the motive power of a weight suspended from a body moving around an axis, is measured by the moment of this weight in conformity to the vertical plane containing the axis. But the notion of proportion between two quantities infinitely small was not at all arrived at maturity when Cardan was writing; he was not able therefore to develop the deduction from which we have just traced the progress; it was possible only to show that the motive power of the suspended weight grows in the same time as its moment or else, as it was done in the Opus novum (23), to admit by intuition the proportionality of these two quantities. The mechanical link that unites the axiom of Aristotle, transformed (24) and become the Principle of virtual velocities, to the theory of moments was not any less clearly perceived; it would depend on the progress of infinitesmal analysis before it would become more rigorous.
We have just seen Cardan bring together some from the many other ideas created or accepted by Leonardo da Vinci and to establish between them a link that this great genius had not perhaps suspected, that he had in any case by no means signalled; elsewhere, we find in the doctor of Milan a faithful interpretation of the thoughts of Leonardo; what is said of the tackle-blocks in the Livres de la Subtilité seems extracted from the manuscripts of which the study has been the object of the preceding Chapter.
- "The fourth example of the subtlety," says Cardan (25), "is in tackle-blocks (26)" After having described a tackle-block in four straps, he adds: "The burden therefore. . . is drawn from above by the fourth part of the force. And if each pulley had three coils, the burden could be drawn by the sixth part of the force; and thus a child will be able to draw from above a great load, unless in such an amount that the weight of the cords, the roughness of the coils, or pullies or tackle-blocks prevent. But for what the proportion of times is to forces and powers, the child will draw by two rolls four times more slowly, by three rolls six times more slowly than he does not draw but would lift from a cord by the same force, thus a little greater, being above, and more slowly more than six times or four times, so much as the length of the cord adds more to the load; therefore it arrives that the child scarcely in one hour will draw and lift the same load by such tackle-block, what a man six times more robust, being above, can lift immediately from a single cord."
Leonardo da Vinci had not applied in detail the axiom of Aristotle but to the lever and to tackle-blocks; in what concerns the screw, he was contented with this brief indication (27): "The more a force extends itself out of a wheel across the wheel, out of a lever along the lever or out of a screw across the screw, the more the force is powerful and slow."
This indication Cardan develops (28) under this title: The manner of pulling and of pushing all things with little force. "By similar manner," says he, "the screws that we call vines are made and composed. . . . So much the more therefore will there be curvings in the screw, and so much more will be low, that is to say nearer to the circumference or beyond, so much the more the weight will be light and the movement easy; and so much the more the movement will be easy, so much the more will be slow. The screw therefore is able to be two cubits from these curvings to such a degree large and low, that the weight will be easily lifted by a child of ten years. But, as I have said, so much the more easily it is moved, so much the more slowly it is drawn and lifted."
This Principle of virtual velocities, Cardan applies, in the Opus Novum (29), to the evaluation of the effect produced by the jack and, in the De Subtilitate (30), to the calculation of "a great machine to lift great loads and heavy weights, which is composed of a screw and a hydraulic cylinder."
In all that touches the Principle of virtual velocities, Cardan developed and completed with sagacity the indications that he would have been able to in the reading of the thoughts of Leonardo da Vinci. He was less fortunate in what concerns the inclined plane. In the De Subtilitate, he does not approach the study of it. In the Opus novum, he has in view (31) to determine the weight of a mobile sphere on an inclined plane, weight that he believes, according to the principle of Dynamics universally admitted in this epoch, proportional to the velocity with which the sphere originated to itself will descend following this plane. As this velocity, nothing when the plane is horizontal, grows at the same time as the angle of inclination of the plane, Cardan believed himself able to state the following proposition: The weight of a sphere which
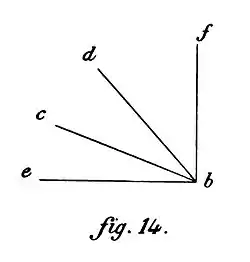
descends an inclined plane is to the weight of the same sphere falling in free fall as the angle of the plane inclined from the horizontal plane is to the right angle.
Although this solution is erroneous, the passage where Cardan expounds it merits being recounted; for he has certainly contributed in suggesting to Simon Stevin on the one hand, and to Galileo on the other hand, the exact solution of this celebrated problem. Stevin, in his Statics, cites and discusses the Opus novum of Cardan; Galileo, when he found for the first time the law of the inclined plane, assuredly had under his eyes the passage that we will cite:
- "Let there be a sphere a of weight g (fig. 14), placed at point b, that one can pull on the inclined plane bc, bf being the vertical plane. On the horizontal plane be, a can be moved by a force as small as one wants, according to what has been said above; in consequence, according to the common opinion, the force which will move a following eb will be nil; on the other hand, according to what has been said, a will be moved towards f by a force always constant and equal to g, in the direction bc by constant force equal to k, in the direction bd lastly by a constant force equal to h; therefore, by the last question, cum termini servent quoad partes eandem rationem singuli per se (32), and as the movement according to be is produced by no force, the relationship between g and k will be as the relationship between the force which moves according to bf to the force which moves according to bc, and as the relationship of the right angle ebf to the angle ebc; and of even the force which moves a according to bf which, according to what has been said, is g to the force which moves according to bd which, by hypothesis, is h, as ebf is to ebd; therefore the resistance to the movement of a according to bd is to the resistance to the movement of the same a according to bc, as h is to k; what one was desiring to demonstrate (33)."
Footnotes
(1) M. E. Wohlwill has expressed in a manner completely incidental, and without insisting on it, the opinion that Tartaglia and Cardan had been subject to, in a manner direct or indirect, the influence of Leonardo da Vinci. — See E. Wohlwill, Die Entdeckung des Beharrungsgesetzes (Zeitschrift für Völkerpsychologie und Sprachwissenschaft, Bd. XIV, p. 386, in note; 1883).
(2) Libri, Histoire des Sciences mathématiques en Italie, vol. III, p. 33. Paris, 1840.
(3) Pacioli, Divina proportione, fol. 1. Venetiis, 1509.
(4) Vasari, Vite..., t. VII, p. 57. Fiorenza, 1550.
(5) Lomazzo, Trattato della pittura, p. 652. Milano, 1585. – Idea del tempio della pittura, p. 17 et p. 106. Milano, 1590.
(6) See, on this subject, Libri, Histoire des Sciences mathématiques en Italie, vol. III, pp. 148ff, Paris, 1840.
(7) Hieronymi Cardani medici Mediolanensis, De Subtititate libri XXI. Ad illustrissimum Principem Ferrandum Gonzagam, Mediolanensis provinciae praefecium. Lugduni, apud Guglielmum Rouiltium, sub Scuto Veneto, in-8°, 1551.
(8) I am not familiar with this edition, except through the mention of it which is made by Cardan in the Apology inserted, in 1530, at the end of Bâle's edition.
(9) Les livres de Hierome Cardanus, médecin milanois, intitulés de la Subtilité et subtiles inventions, ensemble les causes occultes et raisons d'icelles, traduis de latin en françois par Richard le Blanc; à Paris, chez Charles l'Angelier, tenant sa boutique au premier pillier de la grand'salle du Palais; 1556, in-4°.
(10) In 1557, the first edition of the De Subtilitate had been quickly taken in part in: Julii Caesaris Scaligeri exotericarum exercitationum Liber XV; De Subtilitate ad Cardanum, Lutetiae, apud Vascosanum, 1557, in-4°. — To the critics of Jules César Scaliger, Cardan riposted, in 1560, in the Apology which terminates the following edition: Hieronymi Cardini, Mediolanensis medici, De Subtilitate libri XXI, ab authore plus quam mille locis illustrati, nonnulli etiam cum additionibus. Addita insuper Apologia adversus calumniatorem, qua vis horum librorum aperitur. Basilicae, ex officina Petra, Anno MDLX, Mense Martio, in-8°. — Beyond the editions that we have just cited, we have found in Bordeaux, at the Municipal Library and at the University Library: 1st two other Latin editions of the De Subtilitate of Cardan: Norimbergae, apud Petreium, 1560 (in-fol.) et Lugduni, apud Stephanum Michel, 1580 (in-8°); 2nd three other editions of the Livres de la Subtilité translated into French by Richard le Blanc: Paris, Lenoir, 1556 (in-4°); Paris, Lenoir, 1566 (in-8°) and Paris, Cavellat, 1578 (in-8°); 3rd three other editions of the Exercitationes of Scaliger: Francofurti, apud Claudium Marnium et haeredes Joannis Aubrii, 1607 (in-8°); Francofurti, apud A. Wechelum, 1612 (in-8°); Lugduni, apud A. de Harsy, 1615 (in-8°). This sole enumeration makes bright to the eyes the extraordinary vogue which the work of Cardan has enjoyed.
(11) Hieronymi Cardani Mediolanensis, civisque Bononiensis, philosophi, medici et mathematici clarissimi, Opus novum de proportionibus numerorum, motuum, ponderum, sonorum aliarumque rerum mensurandarum, non solum geometrico more stabilitum, set etiam variis experimentis et observationibus rerum in natura, solerti demonstratione illustratum, ad multiplices usus accommodatum, et in V libros digestum. . . . Basileae, ex. officina Henricpetrina, Anno Salutis MDLXX, Mense Martio.
(12) Cardan, Les Livres de la Subtilité, translated from Latin into French by Richard Le Blanc. Paris, l'Angelier, 1556, p. 32.
(13) Les Manuscrits de Léonard de Vinci, published by Charles Ravaisson-Mollien; Ms. A of the Library of the Institute, fol. 20, recto. Paris, 1881.
(14) It is necessary to understand by cd the surface of the luminous image formed in the focal plane of the mirror.
(15) Les Manuscrits de Léonard de Vinci, published by Charles Ravaisson-Mollien; Ms. G of the Library of the Institute, fol. 89, verso. Paris, 1890.
(16) Cardan, Les Livres de la Subtilité, translated from Latin into French by Richard Le Blanc. Paris, l'Angelier, 1556, p. 83.
(17) Les Manuscrits de Léonard de Vinci, published by Charles Ravaisson-Mollien; Ms. F of the Library of the Institute, fol. 67, verso. Paris, 1889.
(18) Cardan, De Subtilitate, Book I, 1st edition, p. 31.
(19) Cardan, Les Livres de la Subtilité, translated from Latin into French by Richard Le Blanc. Paris, l'Angelier, 1556, p. 17.
(20) Cardan, Opus novum, Propositio XCII. Basileae, 1570, p. 84.
(21) Cardan, Opus novum, loc cit.
(22) Cardan, Les Livres de la Subtilité, translated from Latin into French by Richard Le Blanc. Paris, L'Angelier, 1556, pp. 16 and 17.
(23) Cardan, Opus novum, Propositio XCVIII. Basileae, 1570, p. 92.
(24) In the Opus novum, a work conceived in his old age, Cardan seems often to forget the transformation that he has effected to submit to the axiom of Aristotle, in order to appeal to this axiom taken under its first form; thus the theory of the lever (a) is exposed to it by a reasoning analogous to the one that one finds in the Mηχανικὰ προβλήματα; elsewhere the influence of this work makes itself felt at each instant in the Opus novum, that Cardan effects by numerous references to the Treatise of the Stagirite.
- (a) Cardan, Opus novum, Propositio XLV: Rationem staterae ostendere. Basileae, 1570, p. 34.
(25) Cardan, Les Livres de la Subtilité, translated from Latin into French by Richard Le Blanc. Paris, L'Angelier, 1556, p. 333 (Book XVII, Des Arts et inventions artificieuses. La manière de lever facilement les fardeaus [Arts and artificial inventions. The manner of easily lifting tackle-blocks]).
(26) The translator says: "On screws, as of the press". He adds a little further: "Some call them tackle-blocks". Cardan says: "pulleys". Neither the text, nor the figure which accompanies it, leave place to any doubt; it well concerns itself with tackle-blocks.
(27) Les Manuscrits de Léonard de Vinci, published by Charles Ravaisson-Mollien; Ms. A of the Library of the Institute, fol. 35, verso. Paris, 1881.
(28) Cardan, Les Livres de la Subtilité, translated from Latin into French by Richard Le Blanc. Paris, L'Angelier, 1556, p. 333.
(29) Cardan, Opus novum, Propositio LXXI: Proportionem levitatis ponderis per virgam torcularem attracti ad rectam suspensionem invenire. Basileae, 1570, p. 63.
(30) Cardan, Les Livres de la Subtilité, translated from Latin into French by Richard Le Blanc. Paris, L'Angelier, 1556, p. 334.
(31) Cardan, Opus novum, Propositio LXXII: Proportionem ponderis sphæræ pendentis ad ascensum per acclive planum invenire. Basileae, 1570, p. 63.
(32) We renounce translating this obscure member of phrase.
(33) Libri, (Histoire des Sciences mathématiques en Italie, vol. III, p. 174. Paris, 1840) has written what follows: "in his Paralipomena, Cardan has given for the first time the parallelogram of forces for the case where the components act at right angles (Cardini Opera, vol. X, p. 516). Lagrange seems to attribute this proposition to Stevin."—I have not been able to audit this affirmation of Libri; on the other hand, it would be imprudent to accept without verification the affirmations of this author; too often, he reads the old texts in a manner a bit superficial and with the desire to find modern ideas there which were not at all yet conceived; he declares, for example (loc. cit., p. 41), on the subject of the manuscripts of Leonardo da Vinci, that "the theory of the inclined plane is found there explained with a great deal of justice" and we have seen what it is necessary to think of this affirmation.—If the affirmation of Libri touching the Paralipomena of Cardan be well-founded, it is certain that Stevin, who was familiar with the Opus novum when he was writing his Statics, could not have been familiar with this other work.