PHILOSOPHICAL
TRANSACTIONS.
May 20. 1684
The CONTENTS.
1. Two remarkable Cases relating to Vision, communicated to the Publisher, by the learned and ingenious Will. Briggs M. D. Fellow of the College of Physicians, and Physician of St.Thomas's Hospital, Lond. 2. The description and use of the Pores in the skin of the hands and feet, by the learned and ingenious Nehemiah Grew, M. D. Fellow of the College of Physicians, and of the Royal Society. 3. An abstract of a Letter from Mr. Anthony Leewenhoeck of Delft, dated Sept. 17. 1683. containing some Microscopical Observations, about Animals in the scurf of the Teeth, the substance call'd Worms in the Nose, the Cuticula consisting of Scales. 4. A Letter from Mr. John Collins to the Reverend and Learned Dr. John Wallis Savilian Professor of Geometry in the University of Oxford, giving his thoughts about some Defects in Algebra.
Sr. I Received some time since an account of a remarkable Case in Vision, from Dr. Peter Parbarn a worthy Physician in Norwich; which because it so rarely occurs, and the like is mention'd but by few Authors, I imagin'd that the following Transcript of two Letters he was pleas'd to send me about it, might not be unwelcom to you, and therefore I took this opportunity of conveying it to your hands.
First Let. I was lately in Suffolk, and there met with a pretty odd but curious case relating Vision; which I thought then had something of Rarity, and continue still in the perswasion. A Gentleman gave me the history of it, and because his Servant, who was concerned in it, was then in the house, I had the opportunity fully to inform my self, and if there be any Questions you would have propos'd, I shall shortly see him again.
The Gentleman propounded the Case himself, to know the Phylosophy of it, and what should be that particulate Figure in his Servants Eye, that he should see to acutely and strenuously in the day, and be just like a post so soon as the Sun set. The young man may be towards 20 years of age, and all the day hath as good a sight, if not better, than any of the family; distinguisheth at as great a distance any object; sees either nigh at hand or far off, or any of the intermediate spaces as well as any body, and with as much vigour and unweariedness; but when twilight once comes, is (as the Proverb says) blind as a Beetle; fees nothing; runs against Gates, Posts or Rails (any thing either higher, lower, or level to his Eye) and cannot without great difficulty direct himself. Neither is all this from the want of any vigorous influence from the Rays of the Sun, as I conceive; or when he is at home and in the house, he tumbles over Stools, runs his head against Doors, and cannot see or direct himself tolerably well either by the greater or lesser lights of the fire and candle; but commits pleasant mistakes, is apt to complement your feet as readily as present you steadily with a glass of Wine, runs his head against his Master's foot when he is to pull off his Boots, and gives them some other diversions afterward about the Fire and Utensils there, which causeth variety of sometimes pity and other whiles laughter.
I confess this odd and unusual case raised my curiosity to view the Boy well and to discourse with him; there is no disease in the Organ that can be observd; no Vertigo or distemper in the head to interrupt or any way intercept the Spirits in their motions, but to all appearance the fabrick of the Organ is very true and exactly well, and never disturbed with fluxes any way.
I did observe the Eye both by day and night, but could not find fault with any part; neither do I think the suspicion well grounded, that he sees better than others by day-light, because of the vigour and plenty of Rays, for then he might have the same benefit from good fires and candles to invigorate the Organ, and contract the Pupil (for so I suppose it is done, because the greater the Sun-shine is, the better those generally see that are short-sighted) but it seems rather to depend-on some of the Humours, tho I can't tell at present on which, having not had time since to consider of it. I tryed him with Spectacles for variety of light, but they did him no service by either lights.
Second Let. I have had a further account of that odd case I acquainted you with in my last. and also receiv'd a Resolution of those Questions you propounded, which I now send you: I have ranged the problems in the order they were sent me.
Qu. 1 Whether the person was so from a child, or any observable occasion? R. He was thus from the first time he was able to take notice of things, and it came without Distempers.
2. Whether any cloudiness at night falls gradually upon him like a Mist, or all at once when Sun sets? To which he replies, that it comes gradually upon him as daylight declines.
3. What effect the several Aspects of the moon have upon him? He says none, for he is always alike.
4. Whether he feels any pain by fire or candle-light? he says not any.
5. Whether worse in the winter than summer? To which he says, he hath not observ'd any difference.
6. Whether upon taking cold he be worse? he says, he never observ'd any mischief by cold.
7. Whether he sweats much at any labour, and so grows worse upon any sudden stopping of the pores toward night? R. He sweats much at work, but finds no inconvenience, neither observes any difference as to his sight in those days when he works hard or not.
So that if you take this account as a true and plain Narrative without any artifice, it may be judg'd veryrare, and is the first case I ever knew of the like kind. I rest, &c.
Thus far the diligent Observer in his account of this unusual case, which I forbear giving you my thoughts upon at present, reserving them for another occasion; and this being so extraordinary an indisposition of the Eye, it may very well deserve a more particular consideration in the Pathology of that part, which I formerly intimated my intentions one day of publishing. And now 1 have the opportunities of making more frequent Observations in the Distempers that part, which I then thought requisite to so great a design (and which were since put into my hands, by the exceeding bounty and favor of his most Gracious MAJESTY, as I must ever own, when he was pleas'd of late to place me in the care of one of his Hospitals here) I think my self in a double manner oblig'd to prosecute a subject, which may be of so great importance to the world. and should gladly receive any account relating to it.
The case now mention'd (though indeed in a different sense from that of a. Hippocrates[1]) is call'd by later Writers Nyctalopia or Nocturna Caecitas, and is accordingly described; with the Remedies for it, by b. Galen[2], c. Pliny[3], d. Foreflus[4], e, Sennertus[5], and f. Joel[6]; to whom I refer the Reader. Cornelius Celjus, (de Medicin. lib. 6. cap. 6. §. 38.) mentions it under the title of Imbecilitas oculorum; but none of all these have given so exact and full a history of it as will be found in the foregoing Relation.
2. To this unusual case I shall subjoyn, another relating to the same subject, which I lately had the opportunity of observing here in St. Thomas's Hospital, together with my worthy friend Dr. William Dawkins (whom I have the happiness to be joyn'd with there) in a Patient we had for some time under our hands.
The case was this; Daniel Wright aged about 19 years, of a sanguine and plethoric Constitution, about the end of the year 1683. was seiz'd with a dizziness and pain in in the upper part of the head, which he told me he could impure to nothing but the excessive cold weather, which then raged with us to extremity. Hereupon having the misfortune to apply himself to an ignorant Pretender to Physick here, a Plaister for his head was only order'd at that time (without any evacuations) but whether it was the Empl. cephalicum cum eupborbio in the Dispens. or any other I could not learn. The Patient upon this grows much worse, the pains of his head more fixt and girding (I suppose from some Spasms or constrictive Motions of the Meninges) to which succeeded convulsive Fits (which were accompanied afterwards with a Tremor upon his Arms and Legs) and upon this all Objects appear'd double to him, from the fibres of the optic nerves being thus distorted from their wonted Parallelism. After this poor young man had been thus tortur'd by his Empirick, and this Distemper for about 3 months, he was taken in as a great Object of charity into our Hospital. Upon his admission I examined his case as particularly as I could, and judg'd (by his seeing all things double thus) that the Optic Nerves were affected, and that it was gone so far that it would probably end in a gutta serena, and accordingly it fell out not long after his being in the Hospital; which confirms me in the Opinion about Vision I formerly communicated to the R. Society. [7]
In this difficult and extraordinary case, where the Patient had been so long afflicted, and the Fits grew daily worse upon him (so that he had several in a day, which he told me made his Life so uneasy, that he did not care what was done with him) we endeavoured by all ways we could to relieve him. Accordingly we order'd the Cephalic Pills, and an Electuary (which we use in the Hospital in Epileptic Cases) which he rcceiv'd much benefit by: he was also (by intervals) bled in the Jugulars and in the Hemorrhoids and by Leeches which also gave him good relief; his head was shaved, blisters applyed to his Neck, and a Scion made sometime after, &c. we endeavouring by all manner of Revulsions to derive the humour another way, if it were possible; but it was too much fixt, and of too long standing, so that about two months after he had been under our care (and now and then not without some prospect of Relief) a Gutta Serena seiz'd on his right Eye, that he could not see at all on that side; but then the duplicity ceas'd and he saw all Objects single again as before, which is another confirmation of the fore mention'd Opinion.
In the mean time the left Eye being still in danger, we further order'd (besides the continuance of the former Electuary) a Fontanel about the meeting of the Sagittal and Lambdooid Sutures, and Cupping-glasses to his Neck and Shoulders, that nothing might be left unattempted that we thought requisite; but it seems these last were omitted, and whilst we were thus felicitous about preferring his t'other Eye a severe Fit siez'd him, soon after which he died. I hapned the day after to be with a Patient out o'th town, and not having timely notice of his death I mist the opportunity of opening the Body; but I was told that in the upper part of his head, neck and shoulders, a great blackness appear'd not long after he was dead (from the settling of the blood I suppose in those parts) which shews that what was last order'd, which was for several days before his death, had been very proper in this case.
What success the Trepan or Salivation might have had here we did not try; tho the former where there is any discharge of matter, and the latter in venereal pains of the head I know succeed well; but these were not chiefly nocturnal, and the Patient (whenever I prest him in the thing) profest to me the contrary, and seeing him so willing to do any thing for a Cure, and being a very sober temperate Youth, I had no reason to suspect him; and indeed he never suffer'd much of those severe and girding pains but when his Fits were upon him.
Thus, Sir, have I sent you a plain Narrative of this extraordinary Case, hoping you will excuse the careless and un-studied dress 'tis sent in; whereby you will further oblige
SIR,
Your very humble Servant
William Briggs.
By Pores, Physicians mean no more, than certain permeable spaces between the parts of a Body. Wherefore, that there are Pores in the skin of every man's Body, is no more to be question'd than whether Men do ever sweat of perspire.
But in the Hands and Feet, they are very remarkable; both in respect of their Position and their Amplitude, hitherto, so far as I know, describ'd by no Anatomist.
For if anyone will but take the pains, with an indifferent Glass, to survey the Palm of his Hand very well washed with a Ball; he may perceive (besides those great Lines to which some men have given Names, and those of a middle size call'd the Grain of the skin). innumerable little Ridges, of equal bigness and distance, and every where running parallel one with another. And especially, upon the ends and first Joynts of the Fingers and Thumb, upon the top of the Ball, and near the root of the Thumb, a little above the Wrist. In all which places, they are very regularly disposed into Spherical Triangles, and Ellipticks; as in the Hand I have caused to be drawn Fig. 1. Upon these Ridges stand the Pores, all in even Rows, and of that magnitude, as to be visible to a very good Eye without a Glass. But being viewed with one, every Pore looks like a little Fountain, and the sweat may be seen to stand therein, as clear as rock water, and as often as it is wiped off, to spring up within them again.
That which Nature intends in the position of these Ridges, is, That they may the better suit with the use and motion of the Hand: those of the lower side of every Triangle, to the bending in or clutching of the Fingers, and those of the other two sides, and of the Ellipticks, to the pressure of the Hand or Fingers ends against any body, requiring them to yield to the right and left. Upon these Ridges, the Pores are very providently placed, and not in the Furrows which lie between them. that so their structure might be the more sturdy, and less liable to be depraved by compression; whereby only the furrows are dilated or contracted, the Ridges constantly maintaining themselves, and so the Pores unalter'd. And for the same reason, the Pores are also very large, that they may still be the better preferred; tho the skin be never so much compressed and condens'd by the constant use and labour of the Hand. And so those of the Feet, notwithstanding the compression of the skin by the weight of the whole Body.
These Pores being thus made and secur'd, are a very convenient and open passage for the discharge of the more noxous and perspirable parts of the Blood. Which by the continual use of the Hands and Feet, are plentifully brought into them. Whence it is, that the sweat of the Feet, in many people, is much more offensive than that of any other part of the Body. And that many Hypochondriacal Men, and Hysterical Women, have almost a continual burning in the soles of their Feet, and the Palms of their Hands. Yet not on the top of their Feet or back of their Hands; which being not so much chafed nor kept so warm, are the less disposed to receive the said noxious parts; and are therefore unfurnished with this kind of Pores.
I Formerly sent some Observations about Spittle, which I find have been Printed in the Lectures and Collections of Mr. R. H. in the year 1678. Since that time l have often observed my Spittle, out of this Consideration, that if there be any Animals dispersed in our Body, they may at some time or other, be emptied out of the Ductus Salivales into the Mouth. But my expectation in this particular has fail'd, for I have perceived no Animals, or other thing in Spittle than what I formerly mentioned. Tho my Teeth are kept usually very clean, nevertheless when I view them in a Magnifying Glass, I find growing between them a little white matter as thick as wetted flower: in this substance tho I could not perceive any motion, I judged there might probably be living Creatures.
I therfore took some of this flower and mixt it either with pure rain water wherein were no Animals; or else with some of my Spittle (having no Air bubbles to cause a motion in it) and then to my great surprize perceived that the aforesaid matter contained very many small living Animals, which moved themselves very extravagantly, the biggest sort had the shape of A. their motion was strong and nimble, and they darted themselves thro the water or spittle, as a Jack or Pike does thro the water. These were generally not many in number. The 2d. sort had the shape of B. these spun about like a Top, and took a Course sometimes on one side, as is shown at G. and D. they were more in number than the first. In the 3d. sort I could not well distinguish the Figure, for sometimes it seem'd to be an Oval, and other times a Circle. These were so small that they seem'd no bigger than E and therewithal so swift, that I can compare them to nothing better than a swarm of Flies or Gnats, flying and turning among one another in a small space. Of this sort I believe there might be many thousands in a quantity of water no bigger-than a sand, tho the flower were but the 9th. part of the water or spittle containing it.
Besides these Animals there were a great quantity of streaks or threds of different lengths, but like thickness, lying confusedly together, some bent, and others streight as at F. These had no motion or life in them, for I well observed them, having formerly seen live-Animals, in water of the same figure.
I observed the Spittle of two several women, whose Teeth were kept clean, and there were no Animals in the spittle; but the meal between the teeth, being mixt with water, (as before) I found the Animals above described, as also the long particles.
The Spittle of a Child of 8 years old had no living Creatures in it, but the meal between the Teeth, had a great many of the Animals above described, together with the streaks.
The Spittle of an old Man that had lived soberly, had no Animals in it; But the substance upon and between his Teeth, had a great many living Creatures, swimming nimbler then I had hitherto seen. The biggest sort were numerous, and as they moved, bent themselves like G. The other sorts of Animals were in great numbers, insomuch that tho the meal were little, yet the water it was mixt with seem'd to be all alive, there were also the long threads above mentioned. The Spittle of another old man and a good fellow was like the former, but the Animals in the scurf upon the teeth, were not all killed by the parties continual drinking Brandy, Wine, and Tobacco, for I found a few living Animals of the 3d. sort, and in the scurf between the Teeth I found, many more small Animals of the 2 smallest sorts.
I took in my mouth some very strong wine-Vinegar, and closing my Teeth, I gargled and rinsed them very well with the Vinegar, afterwards I washt them very well with fair water, but there were an innumerable quantity of Animals yet remaining in the scurf upon the Teeth, yet most in that between the teeth, and very few Animals of the first sort A.
I took a very little wine-Vinegar and mixt it with the water in which the scurf was dissolved, whereupon the Animals dyed presently. From, hence I conclude, that the Vinegar with which I washt my Teeth; kill'd only those Animals which were on the outside of the scurf, but did not pass thro the whole substance of it.
In many of my foregoing Observations, I saw some clear shining Particles, whereof some were round, others somewhat irregular, of several bignesses, and the largest about 25 times the bulk of a blood-Globule, these if they had not sunk in water, I should have taken for Particles of fat.
The number of these Animals in the scurf of a mans Teeth, are so many that I believe they exceed the number of Men. in a kingdom. For upon the examination of a small parcel of it, no thicker thana Horse-hair, I found too many living Anima's therein, that I guess there might have been 1000 in a quantity of matter no bigger then the 1/100 part of a sand.
A certain man being said to have worms taken out of his face. I took a quantity of these imagined worms, which I laid upon a clean Glass, that I might view them at my leisure. I found them not to differ from what I gave an Account of in my Letter of the 4th of Novemb. 1681. unless it were that some of the hairs in these supposed worms were so tender, that they broke in two upon the least touch, Other worms seem'd to be a bundle of hairs, but when I went to seperate them, it was just as if I had toucht a' soft fat body.
I squeezed some black specks out of the thick of my own Nose, which I saw to be bundles of hairs, I then took out hairs from one of them to the number of 36.
Fig. A. B. C. D. E. is a bundle of hairs, as it appears in a Microscope, the part A. B. C. before I took it out of my Nose, lay even with the skin, and appear'd like a black speck; the hairs were not all of a length, but one stood out more than another, as at B. a single hair standing out as B. was transparent, and in the lower part oi the bundle C. D. E. A. all the hairs together were transparent. parent. In some bundles of hairs the part next the skin lay quite even, as if it had been cut with a pair of sizers. B. D. were the roots of hairs, lying one of them deeper than another.
I took the worms out of the Noses of 2 other persons, and I found the number of hairs in a bundle, to be from 3, 4, 5, 6, and 9. to 25, and 30. when the worms lay deepest in the Nose, they seldom contained any hairs, unless the person they came from were very black, and then the hairs were more easily perceivable.
In the pressing out of worms, I could tell whether there were hairs in them or no, for if the substance came out streight, then there were always hairs, but if bended and bow'd, none.
The make and conformation of these worms, I suppose to be after this manner. When the Root of a hair lying deep in the skin, supplies so much nourishment as to make the hair grow out and appear upon the face, the upper part of the hair by rubbing, or some other violence, comes often to be broke off, the Trunk of it still remaining in the skin. When new matter is supplyed, another hair grows by the side of the former, that was broken; and this so often till there comes sometimes to be 8.10.20. or 36. in a bundle. Yet this number is not made up in 1. or 2. years, but probably in a great many.
The reason of this my conclusion, is grounded upon the bluntness of the tops of all the hairs found in these worms, whereas all the other hairs growing upon the face are sharp-pointed, till such time as they come to be broken.
In the year 1674. I writ to Mr. Oldenburg that I found the Cuticula, or uppermost skin of a body to consist of round Particles or Scales: I also gave him my Opinion, how this skin was made, and how the upper part of it was worn off, and the under part to succeed in its place.
Since that time there was little difference in what I observed, until now of late, that I have made use of another way. For at first I saw by a common Microscope the parts of the Scales appearing to the Eye as they were round, lying close in order, and so small that a sand would cover 200, or 250, of them, as is here shewn in Fig. H. But examining them since, by a Glass which magnified more, I am satisfied that they are not made out at the grosser part of the moisture or sustance which is evaporated out of the body, as I formerly thought, but are meer Scales, such as grow upon the outward skin of a fish, and are called fish-scales.
These Scales lye upon our body just as they do upon fishes, the most part of them are guingue-lateral, the figure of a whole one is here shewn by a magnifying Glass at K the side O. P. was falt'ned to the skin, and is not so broad as if it be measured higher. Some of the Scales were not so long as K. and some had not the sides so even, but these last I took to be pulled off the body before they were fully grown. They are very thin, for I judge their bredth is above 25 times more than their thickness. They lie three deep upon the body, every part being covered with 3 scales succesively, tho not above 1/3, part of a scale discover it self to the Eye, the other 2/3 parts being hid by the other scales. As Fig. M. where the part exposed to view is marked 1, 2, 3, 4. the rest is covered by other scales. The point 3 is not always so sharp as I have here made it, but it being like the Original, which seem'd a perfect scale, I would not alter it.
The scales of Fishes also appear but in part, to the Eye, but it is very observable tho fishes never change their scales; yet men do often. Particularly I instance in my self at this time, being the first of September. That the scales came off me not by one and one, but 1000 in a Cluster. When I pluck off a scale from my body which sticks fast, and perhaps is but newly grown, there comes blood after it, or at least there remains a red spot,
I took off the skin from a scar in my Arm, caused by blood-letting 25 years since, and found the scales to have the shape of L.
Thro many of the aforesaid scales, there run transparent lines, in an odd manner, as at M. and these lines are sometimes stuck with round Balls, of the bigness of 1/6 a blood-globule, as may be seen in the same Figure.
These lines, I believe are caused by the sweat of the body, bringing with it some gross substances which adhere to the scales; the Globules also may either come whole out of the body, or else be made afterwards out of the matter which is evaporated.
It's easy to conceive how a Louse, Flea, or other infect may thrust his sting or snout into the skin, for they need not do it thro the scales, but between the Plates or Mailes.
From hence also may be gathered, that there are no pores in the Cuticula, for the conveying out of sweat, because that may owze out from between the scales, tho they stick never so close together, without supposing that there are channels made for its passage: Let us only reckon how many Vacuities a Scale has, whereby it is nourisht so as to grow, and that in the space of 1/3 part of a scale there may be 100 such Vacuities, thro which the humours of the body may pass, and that 200 such parts of a scale may be covered with a sand. It will follow then, that the body may exhale out of 20000 places in a quantity no bigger then what a sand will cover.
Hereout might be concluded that our Body is nothing but a Pore, notwithstanding what our Physicians speak of the Pores or passages for sweat, as if there were such places contriv'd by Nature for nothing else. For a drop of sweat though by the pressure of the Air it becomes round, yet it may be compounded of Particles coming from many thousand places.
I took some scales coming from the inward and most callous part of the hand, and found them of the same circumference with them of my Body, but as the one sort were very clear and transparent, so the other were so full of lines and so thick beset with Globules, that they seemed to be composed of nothing else; now we find by experience that the hand not only between the fingers, but in the hollow of it, is subject to be moist, more than other parts of the body; so that tho the scales fall off from the other parts of the body for want of nourishment, yet the scales upon the hands and feet are still kept on by a clammy moisture and fat, which being brought to that place to be evacuated, sticks to the Scales, and keeps them together, leaving only some small out-lets for the thinnest of the matter. By this means the skin of the hand, tho it be nothing but scales, comes to be of an extraordinary thickness, which may be increast by hard labour, whereby the moisture is brought into those parts, and the scales are more
packed and clotted together. 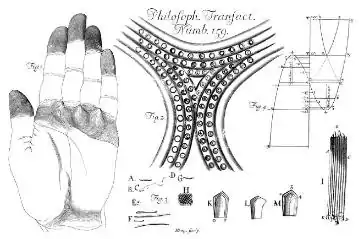
(Upload an image to replace this placeholder.)
TO describe the Locus of a cubick Equation.
A Cardanick Equation convenient for the purpose, (viz. such as shall have the dioristick limits rational) must have the Coefficient of the roots to be the triple of a square number such is a³-48a=N.
Assume a rank of roots in Arithmetical progression, and raise resolvends thereto a³-48a=N or resolvends.
| R | N | ||
| Such are | 1 | 1 | -48=47 |
| 2 | 8 | -96=88 | |
| 3 | 27 | -144=17 | |
| 4 | 64 | -192=128 | |
| 5 | 125 | -240=115 | |
| 6 | 216 | -288=72 | |
| 7 | 343 | -336=+7 | |
| 8 | 512 | -384=+128 | |
| 9 | 729 | -432=+297 |
Draw a Base line and a perpendicular thereto, and from O in the Base line prick the negative resolvends downwards, and the affirmative ones upwards, and raise their roots upon them as ordinates, a Curve passing through the same is one Moity of the Curve or Locus on the right hand for affirmative roots, and the other moity on the left hand is described in the same manner by assuming a rank of negative roots, and raising resolvends thereunto. The Curve Fig. 4. may give a resemblance of the thing.
And 16 the third part of the Coefficient of the roots cubed is equal to the square of 64 half the resolvend, or dioristick limit. Which in composing of Cardans canon is always substracted from the square of half the absolute, as in the example following.
If I were to find the root belonging to the resolvend 297
The square of half thereof is 22052¼
The square of 64 half the dioristick Limit 4096
The difference is 17956¼
And the rule is 148½ + √17956¼.
148½ + √17956¼.
That is in a quadratick Æquation, if 297 were the sum of the two roots and 64 the root of the Rectangle: then if from the square of half the sum, the rectangle be subducted, there remains the square of half the difference of the roots, and giving them an universal Cube root, it is. 3 3
vr48% 'l'V179§ 5f 'l' v I4-8%-~v1r8s619to 9 theroot fought. In the former Scheme, QB and QP. may signifie the roots of Cardam Binomial; that run infinitely upward, and terminate at Q, as is mentioned in Sectim fbe pb. And if they can be continued downwards, probably they will terminate at 0, and H. The $0146/E line in Section 2.-1. may here be represented by the line 9 S. and the Chord line between 9 and ¥> by if from whence tis plain that any root between 9 and 8 found near, may be limited by Approximations of Majm and Minus. As ru CAZ{DAlK§ RULES”
1 The description of the Low: is before handled. 2 The tout/5 line affording approaches by an [Equation derived ourof that proposed is before described, and the method of drawing is mentioned by DMWHM in theTranfactions-3-The Limits are of two kinds (fain) either the in/e limits when the resolvent is O~ and the equation falls a dcg1'€€ lower: or the dim/hc/1 limits whereby a pair of roots gain or loose their poffibility, as is before described. 4. Car/lon; canons are but the sum of the roots of a solid quadratic equation arising out of half the diar;{li¢l= limit as the v of the rectangle, and the resolvent as the fumm 5' If the roots of those lfimmmlf are separately Erickt down as ordinates on their rejolizfenigtlqey begat cur-réf infinitely continued upward, and meeting in a point bisecting the root that is equal to a 'pair of equal roots, when the equation is Juli: limited, or dioristick as aforesaid in the Figure at, Q 6 If these /fimwwlr are prickt down as ordinates to their rcfolvends, Mr. 1Qu/ran upon sudden thoughts, supposed they may describe both sides of an H)']'CTb0!¢. 7 If so they cannot be continued downwards, but by the method in Mercator: Logaritbmotcchnia: most: numbers of a conilant habitude belonging to any arithmetical progression, may by aid of the differences, and a Table of Figurative numbers (yea, and I add otherwise) be continued upward or downward, and if these run downward they will probably end both in the bafé limits at'O and R.
8 If these binomial Cf/5Y'U€5 be continued downward, and separately found should always added make the root of a cubick Equation capable of 3 roots: then Cardam impossible or negative ro0ts are prov'd possible, and we only in ignorance how to extract them.
9 Assume any root within the limits of 3 possible roots, and raise a resolvent to it, and when you have done, by Cnrclanu Rules improved; you may find that root, and, with a little varying the same, both the other roots (as in the Postscript): for every number or magnitude capable of a cube root, is capable of two more, see Section the 11th. following.
10 If the roots in the former Section, be assumed in Arithmetical progression, and the equation with its several Resolvends be depressed, there will come out a regular Series of Quadratick Equations, whence an easie method will rise of writing down such ranks as multiplied by an Arithmetical progression, shall always beget the same cubick equation, the Resolvend only varying.
11 Let the roots of this series of quadraticks be found as usual in binomials, let these binomials be cubed, and then let it be observed, whether the results are constant portions of the square of the Resolvend and of the dioristick limit: and if so, Cardans Rules will have their defect supplyed.
12 In breaking biquadratick, 'tis asserted that by leaving the Resolvend at liberty, it may be infinitely and rationally done, without the Aid of the separating cubick Equation.
13 But Supposing such separating cubick in store, of which Bartholimus in his dioristick hath given us great furniture in Spicies, why may not several roots of that equation be assumed rational, and thence the biquadratick broken into as many pairs of quadratick equations?
14 May not from hence a method arise of writing down 2 Series of quadraticks that multiplied together shall always beget the same biquadratick Nomes, the Resolvend only varying? and hence the Locus of the equation is easily described.
15 Here again (as in the 11) if the binomial roots of these quadraticks be squaredly squared, and those results are constant portions of the cube of the Resolvend, and the dioristick limit; it will be certain there may be general surd Canons for equations of the 4th. dimension, and Monsieur Cluverius (now at London) positively asserts he hath a general method to obtain them for all Dimensions.
16 As Cardans are surd canons deriv'd from the Resolvend, and dioristick limit, so it were worthy disquisition, whether other furd Canons (of which many are fitted to particular cases by your self, Leibnitz and others) do not arise out of the limits of those particular cases and equations, and whether the glimpse of a general Method might thence be deriv'd for all other equations, though encumbred with negative quantities? which Mr. Gregory, a little before his death, said he had attained.
17 The Learned Dr. Pell hath often asserted that after the Limits of an equation are once obtain'd, then it is easy to find all the roots to any Resolvend offer'd.
Now for instance (according to Huddens method) in a biquadratick equation you must multiply all the terms beginning with the highest, and so in order by 4, 3, 2, 1 and the last term or Resolvend by O. whereby it is destroyed, and you come to a cubick Equation, the same as Harriot uses to take away the penultimate Term of the biquadratick, the roots whereof being found, and as roots having Resolvends raised thereto in the biquadratick Equation, are the dioristick Limits thereof.
18 And if this easy method were known, we may come down the Ladder to the bottom, and fall into irrational quantities, and ascend again. Against which assymetry, an Equation might be assumed low, as rational quadratick, and thence a cubick Equation formed, whole limits should be found by aid of the quadratic Equation, and out of that cubick a Biquadratick Equation, whose limits should be found by the aid of that cubick Equation, &c.
19 Equations may be so continued of two Nomes, that both the dioristick and base limits, should be rational, then supposing such Equation incomplete, the increasing or diminishing the roots, fills up all the vacant places.
Q. Whether or in what place one or both sorts of Limits shall loose their rationality? And what is the nature of the roots thus drawn? in this I think you have already determined in divers of your surd Canons.
20 What Dr. Pells method mention'd in Section 17 should be I cannot guess, unless it be either.
To make surd Canons. Or good approaches.
Or that raising Resolvends out of assumed roots, those should make a store from whence to derive the roots of the Resolvend offered.
Or making quadratick Equations out of the dioristick and base limits, those might be interpoled, by aid of a Table of figurate numbers, or otherwise thereby, as in quadratick Equations to attain two roots of a biquadratick at once. which if performed the greatest difficulties are overcome, and why should not this seem probable, in regard the Curve or Locus, be the Equation what it will, makes indented porches.
21 Suppose I should propound two cubick or biquadratick Equations, in both whereof all the signs are +. It is propoundded out of these two, to derive a third Equation, whose root shall be the Summm, Difference, or Rectangle of the Roots of the two Equations propounded. This Mr Gregory a little before his death writ word he had obtained and in the following Series for finding the Moity of a Hyperbolick Logarithm I suppose made use of. From a number propos'd fubllraél: an Unit, let that be Numerator, and to it add an Unit, let that be Denominator and call that fraction N.
s as 1 9 H is
Thgn N1-i+1r+N+N+N+N, ée. 15
I 2 f 7 i II .13
Equal to half the Hyperbolick Logarithm fought. EXAMPLE in the Number
TheFra<9cionis§ I, 3333333===33;33g3 3, 370370:-=-' 123456
5, 41 1 >'1== 8230
The Rank 1§ 7 is easily 7, 4-)'7z==:= 5.5-3 made by dividing ev'ry 9, SO 8=== 5 6 precedingnumberby 9.11, 562: 5-13, 6==:= o
3465733
6931466 which is
Thg Hypcrbolick Logarithm of 2 fought. I want time to consider the prrmifes, but hope you will, (in re ard you seem to think it strange that any diflicnlrieg houlg remain about Cubielgs that are not presently resolved) your considerations wherein will be very acceptable and worthy Publick view-Other
Other Series in Print of M€Yfdl07f,4 dc- dispatch not as this doth neither thereby can the Logarithm of 1 be ealil y made, but by making the Logarithms of such mixt nnmbersor fractions that multiplied together make the result 2 just as zxr;:=3; whence having and finding that of 15, you presently have the Logarithm of 3.»2
2 A Cardanuk Equation that is a Cnbick one wanting the second term, may be multiplied or divided by a rank of continual proportionals, so as to render the coefficient of the roots canonick, that is, to make it the same with the }Equations of the Table, that find the Sine, Tangent, or Secant oi' the third part of that arch to which any Sine, Tangent, or Seeant is pro ounded, and so finding the roots in the tables, those fought are thence obtained by Multiplication or Division- Yea, and the coefficient of the roots may in like manner be rendred an Unit, and then the Resolvends fought in a table of the sums or differences of the Cubes of numbers and their roots, shall help you to Inch roots, as multiplied or divided as aforesaid shall be the true ones fought.
23 It is an enquiry worth consideration, whether two of the roots of a biquadratick may not be kept constant, and the rest be en creased or diminished, either Arithmetically, or by multiplication and diyiiiou in a known Rana? certainly regular Progreilions will arise, though as yet, we cannot cncrcaie create the true roots of an IEquation without as much di miuilhing the Negative. nor can we multiply or divide the roots without we alter all of them. and consequently cannot reduce ooeilicients to such habitues as are' delirabllr. 14. It is a pleasant concmnity out ot a root to raise a Reiblvend iblvend without railing any of the Powers of the root, and at the same time without a thorough binomial Division to depress the Equation a degree lower.
EXAMPLE
Let the Equation be a 1* to a 'l'6a 'l' zoa;: -1072.
Let the root be 4, the resolvent is thus raised by adding the coefficients as you go, and multiplying by the root, thus -I-45' I 0', § .1fQ.I1[4, X4 "7"i'§ 6.§ .6. ', § .~62X4- »»2f§ Xl' 2o“'~;.(>8;»{4, 1',7v, , with the same work the Equation may be depressed without Division.
EXAMPLE
Let the Equation be as before, and place the root with the former products underneath respectively, the summ is the depressed Equation. ai. + lou; J, gal” zca- ~I'~ 71.7170 T4. 'l'5'6'l'24f8 l'1C77.
The sum 8.4-'l'I4 h 'ii 6 z d+z6 S:i::;o. that is divided by a. 14:1 1' 62 a1'z6 5321* o. which is the under ZEquation fought found without Division
25 It's conceived that al1 Equations maybe so regulated as robe reduced tons mam/Arithmetical Progrellion sol multi pliers in whole numbers, asthelF uation hath dimensions, whereof one of the progressions shall be a Seriesot'roots= hence the raifiiiglleiolveiitlsby tentative work is rendred Logarithmetical mb e c, .., N
J:'orExam plc write down any; arithmetic all'rogrefiioi1s, 'w%-R R lr
1X6X3
2X7Xf
3X8X7' fl§
fliiifyo Fhmigenm Rc'omp¢wmw1<k of a cubiclg Efiquation, ”"““1 8 2 1 say the Rank II. are the Reknlvends or 168§ 'Wl10l'C roots are the Rank R. Thiscuhiek jiz quation is easily attained out of the d1l'lerenx 4 A 1, ~
yxi x'~>g golces of the Rank R. for out of the Rank R in any Æquation proposed raise separately the respective powers (with regard to their Cocllicients) and out of the three ~ ~ "'i t n
ag ranks so raised compose their rcipective 1 erenccs, fl 21.3 they shall be the same with the differences of the rank 11 5 of Resolvends or Homogenea Campamrivnw here noted by H. If such Equation be cncombred with fractions they are all removed at once, by multiplying most conveniently, b the least; number that is divisible by the Denominators of fnc fractions, hence also the infinite Series before mentioned (and others) are reduce able to Lo arithmg. 26 Where IE nations have all tieir terms adfecfted with the Eimefign boili 'tor -) Mn Nwvtffn and Mr- Gregor] deceased have atlirmed they are all reduce able to tome pure high power, which is of singular use in the infinite Series. And a Learned ivrman where this cannot be done, hath afiertcd ierted that they may be reduced to a higher power, with a variable Coellicient. which is the root fought with ¥lCOIll° adi lend or fubd- icend. And even this would renderan ealy tentative l, ()g;l, l'l€lllIlCflCl1l way for attaining the root.
27 ll' but o in Rootof an [Equation can be found ata time, then queitioulefs a better Method is not yet attained, then what is mentioned in the printed proposal about Printing Mr. lf»¢»€¢'rf 'I'reatii7:s therein mentioned
28 Lastly, as to Conltrnctions tor Illquations, the following Problelne seenis to be universal.
Any two analytic ='iuf'1/ef (vi#—) such as wherein the Habitude between the Bafe and Ordinate may be expressed by an Equation being given in Magnitude and Pohtion, and from the points of theirinterlection ordinates let tall to the Am of either figure, or upon parallels to the said ./bm, the inquiry is of what [Equation those ordinates are the roots P Dr Barre." liked the proposition as well grounded, and left a discourse about doing itin the conick Sections, in which there .ire 3 eaies, either the axes are parallel or being produced concur, beyond the vertexes of the figures without; or other wile intellect: within the figures. .i4r, (;1-/guy entred on the Rune contemplation, but death deprived us of the benefit of his thong; its
Of Analytick (alias Geometrick) Curves there are innumerable forts. ofwhiffh I shall mention one or two kinds. Between an Arithmetical l'rogreHion and its iiluares, or between its filuares and its cubes. or its cubes and Biquadratics, there may be inter poled as many Arithmetical or Geometrical means as you pleale I and thence /.im or <;'m-z/ei ¢l¢ 1'lViLl, which some call i'f1m§ 1c/ni'/f OF l'¢¢r.fzbc//1//<rf, /ICQ G7'0g/)}'iC$ Ucometrzae, mrs mln/cr/aléf P1-jntgd in Img/ in Q, iQ11'[().
Postscript explaining Section the 9th.
After you have obtained the Cube roots of Cmlwf Binomials, according to Vw Svbn-fm, in D f tin, i or Kei;/w, if you change the Sines of the rational parts of those roots, as also the Sines of, the Radical Parts, and multiply those parts by g, the results are also roots of the cubick Equation first proposed
EXAMPLE.
—1. I 21-'-7-O: 1°fO The cube Roots of the Binomials are ral Hx;—2 2%~~- "E Their fumm is the Root fOllgl1lI°;.'”°. °:l" y "l And the other two Roots are »~f~ 2; V15 zl-.-VZ 3 4 Also in this Equation;~-~6<>a~—<2';'fO The Binomial Roots are +4 +V-4.
- 4—~V°4~
Hence the Root fought is +8 And the other two roots are—4+V4- 1 2 t ~-»- 4—vm
ADVERTIEMENT.
These papers were sent by Mr. Ctllim to Dr. M411/13- in a Lefter of 3 Ui*-rw 1681, (with this Character, I bfwejénfyvu berewith my thoughts about /bm: dqééls in AQ#/fra:) and are 2. Copy of what he had written to some other (but I know not whom) to whom he speaks all along in the second pcrfon, whereas ot others he ipeaks in the third person- And he did intend (had he lived lon er) to perfect it further; by omitting some things which F though here he notes as defects) he found after to be done already, and supplying some others. But he lived not to perfecft it, and therefore (that it be not 1091) WC here give it as we found it.
OXFORD,
Printed at the THEATER, and are to le fold by M&f '7>in, at the *Ang*/, and Samuel Smith, at the Princes Arms in St. Paul's Church-yard LONDON, 1684.
- ↑ In Porrhet. lib. 2. §. 40.
- ↑ Ser Galende Ocul. Part 6. cap. 10.
- ↑ Plin. nat. hist. lib. 8. cap. 50.
- ↑ Fores. lib. 1. abserv. 38.
- ↑ Sennert. lib. 1 part. 3. sect., 2, cao, 44.
- ↑ Joel practic. lib. 2. Sect. 1. §. 10.
- ↑ In Philos. Collect. No. 6 & Transact. No. 147.