An image should appear at this position in the text. A high-res raw scan of the page is available. To use it as-is, as a placeholder, edit this page and replace "{{missing image}}" with "{{raw image|Euclid's Elements 1714 Barrow translation.djvu/26}}". If it needs to be edited first (e.g. cropped or rotated), you can do so by clicking on the image and following the guidance provided. [Show image]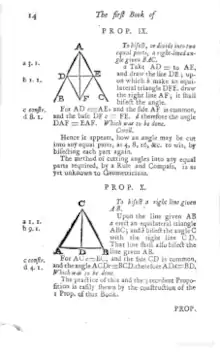

To biſect, or divide into two equal parts, a right-lined angle given BAC.

aa 3. 1.
b 1. 1. Take AD = to AE, and draw the line DE; upon which b make an equilateral triangle DFE. draw the right line AF; it ſhall biſect the angle.

For AD cc conſtr.
d 8. 1. = AE, and the ſide AF is common, and the baſe DF c = FE. d therefore the angle DAF = EAF. Which was to be done.

Hence it appears, how an angle may be cut into any equal parts, as 4, 8, 16, &c. to wit, by biſecting each part again.

The method of cutting angles into any equal parts required, by a Rule and Compaſs, is as yet unknown to Geometricians.

An image should appear at this position in the text. A high-res raw scan of the page is available. To use it as-is, as a placeholder, edit this page and replace "{{missing image}}" with "{{raw image|Euclid's Elements 1714 Barrow translation.djvu/26}}". If it needs to be edited first (e.g. cropped or rotated), you can do so by clicking on the image and following the guidance provided. [Show image]

To biſect a right line given AB.

Upon the line given AB aa 1. 1.
b 9. 1. erect an equilateral triangle ABC; and b biſect the angle C with the right line CD. That line ſhall alſo biſect the line given AB.

For AC cc conſtr.
d 4. 1. = BC, and the ſide CD is common, and the angle ACD c = BCD. therefore AD d = BD. Which was to be done.

The practice of this and the precedent Propoſition is eaſily ſhewn by the conſtruction of the 1. Prop. of this Book.