Page:Calculus Made Easy.pdf/241

This page has been proofread, but needs to be validated.

FINDING AREAS BY INTEGRATING

221

Volumes by Integration.

What we have done with the area of a little strip of a surface, we can, of course, just as easily do with the volume of a little strip of a solid. We can add up all the little strips that make up the total solid, and find its volume, just as we have added up all the small little bits that made up an area to find the final area of the figure operated upon.

Examples.

(1) Find the volume of a sphere of radius $r$ .

A thin spherical shell has for volume $4\pi x^{2}dx$ (see Fig. 59, p. 216); summing up all the concentric shells which make up the sphere, we have

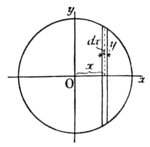
volume sphere $=\int _{x=0}^{x=r}4\pi x^{2}\,dx=4\pi \left[{\frac {x^{3}}{3}}\right]_{0}^{r}={\tfrac {4}{3}}\pi r^{3}$ .

Fig. 62.

We can also proceed as follows: a slice of the sphere, of thickness $dx$ , has for volume $\pi y^{2}dx$ (see Fig. 62). Also $x$ and $y$ are related by the expression

$y^{2}=r^{2}-x^{2}$ .

This article is issued from Wikisource. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.