Page:Calculus Made Easy.pdf/239

This page has been proofread, but needs to be validated.

FINDING AREAS BY INTEGRATING

219

Example. The curve $y=x^{2}-5$ is revolving about the axis of $x$ . Find the area of the surface generated by the curve between $x=0$ and $x=6$ .

A point on the curve, the ordinate of which is $y$ , describes a circumference of length $2\pi y$ , and a narrow belt of the surface, of width $dx$ , corresponding to this point, has for area $2\pi y\,dx$ . The total area is

${\begin{aligned}2\pi \int _{x=0}^{x=6}y\,dx&=2\pi \int _{x=0}^{x=6}(x^{2}-5)\,dx=2\pi \left[{\frac {x^{3}}{3}}-5x\right]_{0}^{6}\\&=6.28\times 42=263.76.\end{aligned}}$ .

Areas in Polar Coordinates.

When the equation of the boundary of an area is given as a function of the distance $r$ of a point of it from a fixed point $O$ (see Fig. 61) called the pole, and

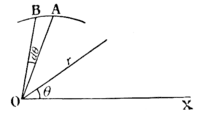
Fig. 61.

of the angle which $r$ makes with the positive horizontal direction $OX$ , the process just explained can be applied just as easily, with a small modification. Instead of a strip of area, we consider a small triangle $OAB$ , the angle at $O$ being $d\theta$ , and we find the sum

This article is issued from Wikisource. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.