Page:Calculus Made Easy.pdf/231

This page has been proofread, but needs to be validated.

FINDING AREAS BY INTEGRATING

211

All integration between limits requires the difference between two values to be thus found. Also note that, in making the subtraction the added constant $C$ has disappeared.

Examples

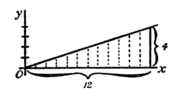
(1) To familiarize ourselves with the process, let us take a case of which we know the answer beforehand. Let us find the area of the triangle (Fig. 53), which

Fig. 53.

has base $x=12$ and height $y=4$ . We know beforehand, from obvious mensuration, that the answer will come $24$ .

Now, here we have as the “curve” a sloping line for which the equation is

$y={\frac {x}{3}}$ .

The area in question will be

$\int _{x=0}^{x=12}y\cdot dx=\int _{x=0}^{x=12}{\frac {x}{3}}\cdot dx$ .

Integrating ${\dfrac {x}{3}}\,dx$ (p. 194), and putting down the

This article is issued from Wikisource. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.