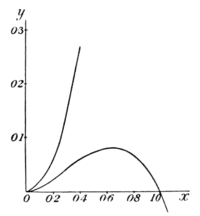
curve goes to the origin, as if there were a minimum there; but instead of continuing beyond, as it should do for a minimum, it retraces its steps (forming what is called a “cusp”). There is no minimum, therefore, although the condition for a minimum is satisfied, namely ${\displaystyle {\dfrac {dy}{dx}}=0}$. It is necessary therefore always to check by taking one value on either side.

Now, if we take ${\displaystyle x={\tfrac {16}{25}}=0.64}$. If ${\displaystyle x=0.64}$, ${\displaystyle y=0.7373}$ and ${\displaystyle y=0.0819}$; if ${\displaystyle x=0.6}$, ${\displaystyle y}$ becomes ${\displaystyle 0.6389}$ and ${\displaystyle 0.0811}$; and if ${\displaystyle x=0.7}$, ${\displaystyle y}$ becomes ${\displaystyle 0.8996}$ and ${\displaystyle 0.0804}$.

This shows that there are two branches of the curve; the upper one does not pass through a maximum, but the lower one does.

(7) A cylinder whose height is twice the radius of the base is increasing in volume, so that all its parts