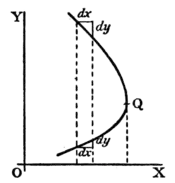
If a curve has the form of Fig. 18, the value of ${\displaystyle {\dfrac {dy}{dx}}}$ will be negative in the upper part, and positive in the lower part; while at the nose of the curve where it becomes actually perpendicular, the value of ${\displaystyle {\dfrac {dy}{dx}}}$ will be infinitely great.

Now that we understand that ${\displaystyle {\dfrac {dy}{dx}}}$ measures the steepness of a curve at any point, let us turn to some of the equations which we have already learned how to differentiate.

(1) As the simplest case take this:

It is plotted out in Fig. 19, using equal scales for ${\displaystyle x}$ and ${\displaystyle y}$. If we put ${\displaystyle x=0}$, then the corresponding ordinate will be ${\displaystyle y=b}$; that is to say, the “curve” crosses the ${\displaystyle y}$-axis at the height ${\displaystyle b}$. From here it