< A Treatise on Painting
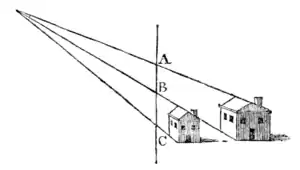
Chap. CCCXLIV.—Why a painted Object does not appear so far distant as a real one, though they be conveyed to the Eye by equal Angles.
If a house be painted on the pannel B C, at the

apparent distance of one mile, and by the side of it a real one be perceived at the true distance of one mile also; which objects are so disposed, that the pannel, or picture, A C, intersects the pyramidical rays with the same opening of angles; yet these two objects will never appear of the same size, nor at the same distance, if seen with both eyes[1].
- ↑ This position has been already laid down in chapter cxxiv. (and will also be found in chapter cccxlviii.); and the reader is referred to the note on that passage, which will also explain that in the text, for further illustration. It may, however, be proper to remark, that though the author has here supposed both objects conveyed to the eye by an angle of the same extent, they cannot, in fact, be so seen, unless one eye be shut; and the reason is this: if viewed with both eyes, there will be two points of sight, one in the centre of each eye; and the rays from each of these to the objects must of course be different, and will consequently form different angles.
This article is issued from Wikisource. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.