It may happen that a colour does not alter, though placed at different distances, when the thickness of the air and the distance are in the same inverse proportion. It is proved thus: let A be the
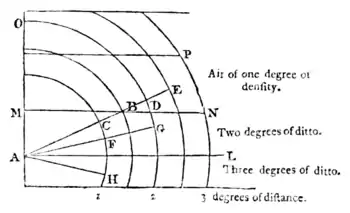
eye, and H any colour whatever, placed at one degree of distance from the eye, in a quality of air of four degrees of thickness; but because the second degree above, A M N L, contains a thinner air by one half, which air conveys this colour, it follows that this colour will appear as if removed double the distance it was at before, viz. at two degrees of distance, A F and F G, from the eye; and it will be placed in G. If that is raised to the second degree of air A M N L, and to the degree O M, P N, it will necessarily be placed at E, and will be removed from the eye the whole length of the line A E, which will be proved in this manner to be equal in thickness to the distance A G. If in the same quality of air the distance A G interposed between the eye and the colour occupies two degrees, and A E occupies two degrees and a half, it is sufficient to preserve the colour G, when raised to E, from any change, because the degree A C and the degree A F being the same in thickness, are equal and alike, and the degree C D, though equal in length to the degree F G, is not alike in point of thickness of air; because half of it is situated in a degree of air of double the thickness of the air above: this half degree of distance occupies as much of the colour as one whole degree of the air above would, which air above is twice as thin as the air below, with which it terminates; so that by calculating the thickness of the air, and the distances, you will find that the colours have changed places without undergoing any alteration in their beauty. And we shall prove it thus: reckoning first the thickness of air, the colour H is placed in four degrees of thickness, the colour G in two degrees, and E at one degree. Now let us see whether the distances are in an equal inverse proportion; the colour E is at two degrees and a half of distance, G at two degrees, and H at one degree. But as this distance has not an exact proportion with the thickness of air, it is necessary to make a third calculation in this manner: A C is perfectly like and equal to A F; the half degree, C B, is like but not equal to A F, because it is only half a degree in length, which is equal to a whole degree of the quality of the air above; so that by this calculation we shall solve the question. For A C is equal to two degrees of thickness of the air above, and the half degree C B is equal to a whole degree of the same air above; and one degree more is to be taken in, viz. B E, which makes the fourth. A H has four degrees of thickness of air, A G also four, viz. A F two in value, and F G also two, which taken together make four. A E has also four, because A C contains two, and C D one, which is the half of A C, and in the same quality of air; and there is a whole degree above in the thin air, which all together make four. So that if A E is not double the distance A G, nor four times the distance A H, it is made equivalent by the half degree C B of thick air, which is equal to a whole degree of thin air above. This proves the truth of the proposition, that the colour H G E does not undergo any alteration by these different distances.