HARMONY (Gr. ἁρμονία, a concord of musical sounds, ἁρμόζειν to join; ἁρμονική (sc. τεχνή) meant the science or art of music, μουσική being of wider significance), a combination of parts so that the effect should be aesthetically pleasing. In its earliest sense in English it is applied, in music, to a pleasing combination of musical sounds, but technically it is confined to the science of the combination of sounds of different pitch.
I. Concord and Discord—By means of harmony modern music has attained the dignity of an independent art. In ancient times, as at the present day among nations that have not come under the influence of European music, the harmonic sense was, if not altogether absent, at all events so obscure and undeveloped as to have no organizing power in the art. The formation by the Greeks of a scale substantially the same as that which has received our harmonic system shows a latent harmonic sense, but shows it in a form which positively excludes harmony as an artistic principle. The Greek perception of certain successions of sounds as concordant rests on a principle identifiable with the scientific basis of concord in simultaneous sounds. But the Greeks did not conceive of musical simultaneity as consisting of anything but identical sounds; and when they developed the practice of magadizing—i.e. singing in octaves—they did so because, while the difference between high and low voices was a source of pleasure, a note and its octave were then, as now, perceived to be in a certain sense identical. We will now start from this fundamental identity of the octave, and with it trace the genesis of other concords and discords; bearing in mind that the history of harmony is the history of artistic instincts and not a series of progressive scientific theories.

The unisonous quality of octaves is easily explained when we examine the “harmonic series” of upper partials (see Sound). Every musical sound, if of a timbre at all rich (and hence pre-eminently the human voice), contains some of these upper partials. Hence, if one voice produce a note which is an upper partial of another note sung at the same time by another voice, the higher voice adds nothing new to the lower but only reinforces what is already there. Moreover, the upper partials of the higher voice will also coincide with some of the lower. Thus, if a note and its octave be sung together, the upper octave is itself No. 2 in the harmonic series of the lower, No. 2 of its own series is No. 4 of the lower, and its No. 3 is No. 6, and so on. The impression of identity thus produced is so strong that we often find among people unacquainted with music a firm conviction that a man is singing in unison with a boy or an instrument when he is really singing in the octave below. And even musical people find a difficulty in realizing more than a certain brightness and richness of single tone when a violinist plays octaves perfectly in tune and with a strong emphasis on the lower notes. Doubling in octaves therefore never was and never will be a process of harmonization.
Now if we take the case of one sound doubling another in the 12th, it will be seen that here, too, no real addition is made by the higher sound to the lower. The 12th is No. 3 of the harmonic series, No. 2 of the higher note will be No. 6 of the lower, No. 3 will be No. 9, and so on. But there is an important difference between the 12th and the octave. However much we alter the octave by transposition into other octaves, we never get anything but unison or octaves. Two notes two octaves apart are just as devoid of harmonic difference as a plain octave or unison. But, when we apply our principle of the identity of the octave to the 12th, we find that the removal of one of the notes by an octave may produce a combination in which there is a distinct harmonic element. If, for example, the lower note is raised by an octave so that the higher note is a fifth from it, No. 3 of the harmonic series of the higher note will not belong to the lower note at all. The 5th is thus a combination of which the two notes are obviously different; and, moreover, the principle of the identity of octaves can now operate in a contrary direction and transfer this positive harmonic value of the 5th to the 12th, so that we regard the 12th as a 5th plus an octave, instead of regarding the 5th as a compressed 12th.[1] At the same time, the relation between the two is quite close enough to give the 5th much of the feeling of harmonic poverty and reduplication that characterizes the octave; and hence when medieval musicians doubled a melody in 5ths and octaves they believed themselves to be doing no more than extending and diversifying the means by which a melody might be sung in unison by different voices. How they came to prefer for this purpose the 4th to the 5th seems puzzling when we consider that the 4th does not appear as a fundamental interval in the harmonic series until that series has passed beyond that part of it that maintains any relation to our musical ideas. But it was of course certain that they obtained the 4th as the inversion of the 5th; and it is at least possible that the singers of lower voices found a peculiar pleasure in singing below higher voices in a position which they felt harmonically as that of a top part. That is to say, a bass, in singing a fourth below a tenor, would take pleasure in doubling in the octave an alto singing normally a 5th above the tenor.[2] This should also, perhaps, be taken in connexion with the fact that the interval of the downward 4th is in melody the earliest that became settled. And it is worth noticing that, in any singing-class where polyphonic music is sung, there is a marked tendency among the more timid members to find their way into their part by a gentle humming which is generally a 4th below the nearest steady singers.
The limited compass of voices soon caused modifications in the medieval parallelisms of 4ths and 5ths, and the introduction of independent ornaments into one or more of the voices increased to an extent which drew attention to other intervals. It was long, however, before the true criterion of concord and discord was attained; and at first the notion of concord was purely acoustic, that is to say, the ear was sensitive only to the difference in roughness and smoothness between combinations in themselves. And even the modern researches of Helmholtz fail to represent classical and modern harmony, in so far as the phenomena of beats are quite independent of the contrapuntal nature of concord and discord which depends upon the melodic intelligibility of the motion of the parts. Beats give rise to a strong physical sense of discord akin to the painfulness of a flickering light (see Sound). Accordingly, in the earliest experiments in harmony, the ear, in the absence of other criteria, attached much more importance to the purely acoustic roughness of beats than our ears under the experience of modern music. This, and the circumstance that the imperfect concords[3] (the 3rds and 6ths) long remained out of tune owing to the incompleteness of the Pythagorean system of harmonic ratios, sufficiently explain the medieval treatment of these combinations as discords differing only in degree from the harshness of 2nds and 7ths. In the earliest attempts at really contrapuntal writing (the astonishing 13th and 14th-century motets, in which voices are made to sing different melodies at once, with what seems to modern ears a total disregard of sound and sense) we find that the method consists in a kind of rough-hewing by which the concords of the octave, 5th and 4th are provided at most of the strong accents, while the rest of the harmony is left to take care of itself. As the art advanced the imperfect concords began to be felt as different from the discords; but as their true nature appeared it brought with it such an increased sense of the harmonic poverty of octaves, 5ths and 4ths, as ended in a complete inversion of the earliest rules of harmony.
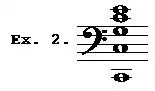 |
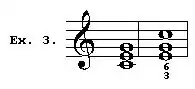 |
The harmonic system of the later 15th century, which culminated in the “golden age” of the 16th-century polyphony, may be described as follows: Imagine a flux of simultaneous independent melodies, so ordered as to form an artistic texture based not only on the variety of the melodies themselves, but also upon gradations between points of repose and points in which the roughness of sound is rendered interesting and beautiful by means of the clearness with which the melodic sense in each part indicates the convergence of all towards the next point of repose. The typical point of repose owes its effect not only to the acoustic smoothness of the combination, but to the fact that it actually consists of the essential elements present in the first five notes of the harmonic series. The major 3rd has thus in this scheme asserted itself as a concord, and the fundamental principle of the identity of octaves produces the result that any combination of a bass note with a major 3rd and a perfect 5th above it, at any distance, and with any amount of doubling, may constitute a concord available even as the final point of repose in the whole composition. And by degrees the major triad, with its major 3rd, became so familiar that a chord consisting of a bare 5th, with or without an octave, was regarded rather as a skeleton triad without the 3rd than as a concord free from elements of imperfection. Again, the identity of the octave secured for the combination of a note with its minor 3rd and minor 6th a place among concords; because, whether so recognized by early theorists or not, it was certainly felt as an inversion of the major triad. The fact that its bass note is not the fundamental note (and therefore has a series of upper partials not compatible with the higher notes) deprives it of the finality and perfection of the major triad, to which, however, its relationship is too near for it to be felt otherwise than as a concord. This sufficiently explains why the minor 6th ranks as a concord in music, though it is acoustically nearly as rough as the discord of the minor 7th, and considerably rougher than that of the 7th note of the harmonic series, which has not become accepted in our musical system at all.
But the major triad and its inversion are not the only concords that will be produced by our flux of melodies. From time to time this flux will arrest attention by producing a combination which, while it does not appeal to the ear as being a part of the harmonic chord of nature, yet contains in itself no elements not already present in the major triad. Theorists have in vain tried to find in “nature” a combination of a note with its minor 3rd and perfect 5th; and so long as harmony was treated unhistorically and unscientifically as an a priori theory in which every chord must needs have a “root,” the minor triad, together with nearly every other harmonic principle of any complexity, remained a mystery. But the minor triad, as an artistic and not purely acoustic phenomenon, is an inevitable thing. It has the character of a concord because of our intellectual perception that it contains the same elements as the major triad; but its absence of connexion with the natural harmonic series deprives it of complete finality in the simple system of 16th-century harmony, and at the same time gives it a permanent contrast with the major triad; a contrast which is acoustically intensified by the fact that, though its intervals are in themselves as concordant as those of the major triad, their relative position produces decidedly rough combinations of “resultant tones.”
By the time our flux of melodies had come to include the major and minor triads as concords, the notion of the independence of parts had become of such paramount importance as totally to revolutionize the medieval conception of the perfect concords. Fifths and octaves no longer formed an oasis in a desert of cacophony, but they assumed the character of concord so nearly approaching to unison that a pair of consecutive 5ths or octaves began to be increasingly felt as violating the independence of the parts. And thus it came about that in pure 16th-century counterpoint (as indeed at the present day whenever harmony and counterpoint are employed in their purest significance) consecutive 5ths and octaves are strictly forbidden. When we compare our laws of counterpoint with those of medieval discant (in which consecutive 5ths and octaves are the rule, while consecutive 3rds and 6ths are strictly forbidden) we are sometimes tempted to think that the very nature of the human ear has changed. But it is now generally recognized that the process was throughout natural and inevitable, and the above account aims at showing that consecutive 5ths are forbidden by our harmonic system for the very reason which inculcated them in the system of the 12th century.
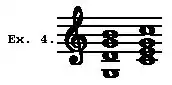 |
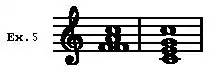 |
II. Tonality.—As soon as the major and minor triad and their first inversions were well-defined entities, it became evident that the successions of these concords and their alternations with discord involved principles at once larger and more subtle than those of mere difference in smoothness and artificiality. Not only was a major chord (or at least its skeleton) necessary for the final point of repose in a composition, but it could not itself sound final unless the concords as well as the discords before it showed a well-defined tendency towards it. This tendency was best realized when the penultimate concord had its fundamental note at the distance of a 5th or a 4th above or below that of the final chord. When the fundamental note of the penultimate chord is a 5th above or (what is the same thing) a 4th below that of the final chord, we have an “authentic” or “perfect” cadence, and the relation between the two chords is very clear. While the contrast between them is well marked, they have one note in common—for the root of the penultimate chord is the 5th of the final chord; and the statement of this common note, first as an octave or unison and then as a 5th, expresses the first facts of harmony with a force which the major 3rds of the chords can only strengthen, while it also involves in the bass that melodic interval of the 4th or the 5th which is now known to be the germ of all melodic scales. The relation of the final note of a scale with its upper 5th or lower 4th thus becomes a fundamental fact of complex harmonic significance—that is to say, of harmony modified by melody in so far as it concerns the succession of sounds as well as their simultaneous combination. In our modern key-system the final note of the scale is called the tonic, and the 5th above or 4th below it is the dominant. (In the 16th century the term “dominant” has this meaning only in the “authentic” modes other than the Phrygian, but as an aesthetic fact it is present in all music, though the theory here given would not have been intelligible to any composers before the 18th century). Another penultimate chord asserts itself as the converse of the dominant—namely, the chord of which the root is a 5th below or a 4th above the final. This chord has not that relationship to the final which the dominant chord shows, for its fundamental note is not in the harmonic series of the final. But the fundamental note of the final chord is in its harmonic series, and in fact stands to it as the dominant stands to the final. Thus the progression from subdominant, as it is called, to tonic, or final, forms a full close known as the “plagal cadence,” second only in importance to the “perfect” or “authentic cadence.” In our modern key-system these three chords, the tonic, the dominant and the subdominant, form a firm harmonic centre in reference to which all other chords are grouped. The tonic is the final in which everything ultimately resolves: the dominant stands on one side of it as a chord based on the note harmonically most closely related to the tonic, and the subdominant stands on the other side as the converse and opposite of the dominant, weaker than the dominant because not directly derived from the tonic. The other triads obtainable from the notes of the scale are all minor, and of less importance; and their relationship to each other and to the tonic is most definite when they are so grouped that their basses rise and fall in 4th and 5ths, because they then tend to imitate the relationship between tonic, dominant and subdominant.
 |
|
Here are the six common chords of the diatonic scale. The triad on the 7th degree or “leading-note” (B) is a discord, and is therefore not given here. The submediant is so-called because if the subdominant is taken a 5th below the tonic, the submediant will come midway between it and the tonic, as the mediant comes midway between tonic and dominant. |
Now, in the 16th century it was neither necessary nor desirable that chords should be grouped exclusively in this way. The relation between tonic, dominant and subdominant must necessarily appear at the final close, and in a lesser degree at subordinate points of repose; but, where no harmonies were dwelt on as stable and independent entities except the major and minor triads and their first inversions, a scheme in which these were confined to the illustration of their most elementary relationship would be intolerably monotonous. It is therefore neither surprising nor a sign of archaism that the tonality of modal music is from the modern point of view often very indefinite. On the contrary, the distinction between masterpieces and inferior works in the 16th century is nowhere more evident than in the expressive power of modal tonality, alike where it resembles and where it differs from modern. Nor is it too much to say that that expressive power is based on the modern sense of key, and that a description of modal tonality in terms of modern key will accurately represent the harmonic art of Palestrina and the other supreme masters, though it will have almost as little in common with 16th-century theory and inferior 16th-century practice as it has with modern custom. We must conceive modal harmony and tonality as a scheme in which voices move independently and melodiously in a scale capable of bearing the three chords of the tonic, dominant and subdominant, besides three other minor triads, but not under such restrictions of symmetrical rhythm and melodic design as will necessitate a confinement to schemes in which these three cardinal chords occupy a central position. The only stipulation is that the relationship of at least two cardinal chords shall appear at every full close. At other points the character and drift of the harmony is determined by quite a different principle—namely, that, the scale being conceived as indefinitely extended, the voices are agreed in selecting a particular section of it, the position of which determines not only the melodic character of each part but also the harmonic character of the whole, according to its greater or less remoteness from the scale in which major cardinal chords occupy a central position. Historically these modes were derived, with various errors and changes, from the purely melodic modes of the Greeks. Aesthetically they are systems of modern tonality adapted to conditions in which the range of harmony was the smallest possible, and the necessity for what we may conveniently call a clear and solid key-perspective incomparably slighter than that for variety within so narrow a range. We may thus regard modal harmony as an essentially modern scheme, presented to us in cross-sections of various degrees of obliquity, and modified at every close so as either to take us to a point of view in which we see the harmony symmetrically (as in those modes[4] of which the final chord is normally major, namely the Ionian, which is practically our major scale, the Mixolydian and the Lydian, which last is almost invariably turned into Ionian by the systematic flattening of its 4th degree) or else to transform the mode itself so that its own notes are flattened and sharpened into suitable final chords (as is necessary in those modes of which the triad on the final is normally minor, namely, the Dorian, Phrygian and Aeolian). In this way we may describe Mixolydian tonality as a harmonic scheme in which the keys of G major and C major are so combined that sometimes we feel that we are listening to harmony in C major that is disposed to overbalance towards the dominant, and sometimes that we are in G major with a pronounced leaning towards the subdominant. In the Dorian mode our sensations of tonality are more confused. We seem to be wandering through all the key-relationships of a minor tonic without defining anything, until at the final close the harmonies gather strength and bring us, perhaps with poetic surprise, to a close in D with a major chord. In the Phrygian mode the difficulty in forming the final close is such that classical Phrygian compositions actually end in what we feel to be a half-close, an impression which is by the great masters rendered perfectly artistic by the strong feeling that all such parts of the composition as do not owe their expression to the variety and inconstancy of their harmonic drift are on the dominant of A minor.
It cannot be too strongly insisted that the expression of modal music is a permanent artistic fact. Its refinements may be crowded out by the later tonality, in which the much greater variety of fixed chords needs a much more rigid harmonic scheme to control it, but they can never be falsified. And when Beethoven in his last “Bagatelle” raises the 6th of a minor scale for the pleasure he takes in an unexpectedly bright major chord; or when, in the Incarnatus of his Mass in D, he makes a free use of the Dorian scale, he is actuated by precisely the same harmonic and aesthetic motives as those of the wonderful opening of Palestrina’s eight-part Stabat Mater; just as in the Lydian figured chorale in his A minor Quartet he carries out the principle of harmonic variety, as produceable by an oblique melodic scale, with a thoroughness from which Palestrina himself would have shrunk. (We have noted that in 16th-century music the Lydian mode is almost invariably Ionicized.)
 |
 |
III. Modern Harmony and Tonality.—In the harmonic system of Palestrina only two kinds of discord are possible, namely, suspensions and passing-notes. The principle of the suspension is that while parts are moving from one concord to another one of the parts remains behind, so as to create a discord at the moment when the other parts proceed. The suspended part then goes on to its concordant note, which must lie on an adjacent (and in most cases a lower) degree of the scale. Passing-notes are produced transiently by the motion of a part up or down the scale while other parts remain stationary. The possibilities of these two devices can be worked out logically so as to produce combinations of extreme harshness. And, when combined with the rules which laid on the performers the responsibility for modifying the strict scale of the mode in order to form satisfactory closes and avoid melodic harshness, they sometimes gave rise to combinations which the clearest artistic intellects of the 16th century perceived as incompatible with the modal style. For example, in a passage written thus the singer of the lower part would be obliged to flatten his B in order to avoid the ugly “tritone” between F and B, while the other singer would be hardly less likely on the spur of the moment to sharpen his G under the impression that he was making a close; and thus one of the most complex and characteristically modern discords, that of the augmented 6th, did frequently occur in 16th-century performances, and was not always regarded as a blunder. But if the technical principles of 16th-century discord left much to the good taste of composers and singers, they nevertheless in conjunction with that good taste severely restricted the resources of harmony; for, whatever the variety and artificiality of the discords admitted by them, they all had this in common, that every discord was transient and could only arise as a phenomenon of delay in the movement of one or more parts smoothly along the scale (“in conjunct motion”) or of a more rapid motion up and down the scale in which none but the rigorously concordant first and last notes received any emphasis. No doubt there were many licenses (such as the “changing-note”) which introduced discords by skip, or on the strong beat without preparation, but these were all as natural as they were illogical. They were artistic as intelligible accidents, precisely like those which make language idiomatic, such as “attraction of the relative” in Greek. But when Monteverde and his fellow monodists tried experiments with unprepared discords, they opened up possibilities far too vast to be organized by them or by the next three generations. We have elsewhere compared the difference between early and modern harmony with that between classical Greek, which is absolutely literal and concrete in expression, and modern English, which is saturated with metaphors and abstractions. We may go further and say that a 16th-century discord, with its preparation and resolution, is, on a very small scale, like a simile, in which both the figure and its interpretation are given, whereas modern discord is like the metaphor, in which the figure is a substitute for and not an addition to the plain statement. It is not surprising that the sudden opening up of the whole possibilities of modern harmony at the end of the 16th century at first produced a chaos of style.
Another feature of the harmonic revolution arose from the new habit of supporting a single voice on chords played by an instrument. This, together with the use of discords in a new sense, drew attention to the chords as things in themselves and not as moments of greater or less repose in a flux of independent melodies. This was as valuable an addition to musical thought and expression as the free use of abstract terms is in literature, but it had precisely the same dangers, and has until recent times vitiated harmonic theory and divorced it from the modest observation of the practice of great masters. When, early in the 18th century, Rameau devoted much of his best energy to the elaboration of a theory of harmony, his field of observation was a series of experiments begun in chaos and resolved, not as yet in a great art, but in a system of conventions, for the contemporary art of Bach and Handel was beyond the scope of contemporary theory. He showed great analytical genius and sense of tonality in his development of the notion of the “fundamental bass,” and it is rather to his credit than otherwise that he did not emphasize the distinction between discords on the dominant and those on other degrees of the scale. But his system, with all subsequent improvements, refutations and repairs only led to that bane of 19th-century theory and source of what may be called the journalese of harmonic style, according to which every chord (no matter how obviously artificial and transient) must be regarded, so to speak, as a literal fact for which a root and a scientific connexion with the natural harmonic series must at all cost be found. Some modern theorists have, however, gone too far in denying the existence of harmonic roots altogether, and certainly it is neither scientific nor artistic to regard the coincidence of the major triad with the first five notes of the harmonic series as merely accidental. It is not likely that the dominant 7th owes all its naturalness to a resemblance to the flat 7th of the harmonic series, which is too far out of tune even to pass for an augmented 6th. But the dominant major 9th certainly gains in sonorousness from its coincidence with the 9th harmonic, and many cases in music could be found where the dominant 7th itself would gain from being so far flattened as to add coincidence with a natural harmonic to its musical significance as an unprepared discord (see, for example the “native wood-notes wild” of the distant huntsmen in the second act of Tristan und Isolde, where also the 9th and 11th are involved, and, moreover, on horns, of which the natural scale is the harmonic series itself). If the distinction between “essential” and “unessential” discords is, in the light of history and common sense, a difference only in degree, it is thus none the less of great aesthetic importance. Arithmetic and acoustics show that in proportion as musical harmony emphasizes combinations belonging to the lower region of the harmonic series the effect will be sonorous and natural; but common sense, history and aesthetics also show that the interaction of melody, harmony and rhythm must produce a host of combinations which acoustics alone cannot possibly explain. These facts are amply competent to explain themselves. To describe them in detail is beyond the scope of the present article, but a few examples from different periods are given at the end in musical type.
IV. The Minor Mode.—When the predecessors of Bach and Handel had succeeded in establishing a key-system able to bear the weight of free discord, that key-system took two forms, in both of which the three chords of tonic, dominant and subdominant occupied cardinal points. In the one form the tonic chord was natural, that is to say, major. In the other form the tonic chord was artificial, that is to say, minor. In the minor mode so firm is the position of the tonic and dominant (the dominant chord always being major) that it is no longer necessary, as in the 16th century, to conclude with a major chord, although it long remained a frequent practice, rather because of the inherent beauty and surprise of the effect than because of any mere survival of ancient customs, at least where great masters are concerned. (This final major chord is known as the Tierce de Picardie.) The effect of the minor mode is thus normally plaintive because it centres round the artificial concord instead of the natural; and, though the keynote bears this minor artificial triad, the ear nevertheless has an expectation (which may be intensified into a powerful emotional effect) that the final conclusion of the harmonic scheme may brighten out into the more sonorous harmonic system of major chords. Let us once more recall those ecclesiastical modes of which the 3rd degree is normally minor. We have seen how they may be regarded as the more oblique of the various cross-sections of the 16th-century harmonic scheme. Now, the modern minor mode is too firmly rooted in its minor tonic chord for the 16th-century feeling of an oblique harmonic scheme to be of more than secondary importance, though that feeling survives, as the discussion of key-relationships will show us. But it is constantly thrust into the background by the new possibility that the minor tonic chord with its attendant minor harmonies may give place to the major system round the same tonic, and by the certainty that if any change is made at the conclusion of the work it will be upon the same tonic and not have reference to some other harmonic centre. In other words, a major and minor key on the same tonic are felt as identical in everything but expression (a point in which the Tonic Sol Fa system, as hitherto practised, with its identification of the minor key with its “relative” instead of its tonic major, shows a most unfortunate confusion of thought). The characteristics of the major and minor modes may of course be modified by many artistic considerations, and it would be as absurd to develop this account into a scheme of pigeon-holed passions as to do the same for the equally obvious and closely parallel fact that in drama a constant source of pathos is the placing of our sympathies in an oblique relation to the natural sequence of events or to the more universal issues of the subject.
V. Key-Relationships.—On the modern sense of the identity of the tonic in major and minor rests the whole distinctive character of modern harmony, and the whole key-system of the classical composers. The masters of the 16th century naturally found it necessary to make full closes much more frequently than would be desirable if the only possible close was that on the final of the mode. They therefore formed closes on other notes, but they formed them on these exactly as on a final. Thus, a close on the second degree of the Ionian mode was identical with a Dorian final close. The notes, other than the final, on which closes could be made were called modulations. And what between the three “regular modulations” (known as the dominant, mediant, and participant) and the “conceded modulations,” of which two were generally admitted in each mode simply in the interests of variety, a composer was at liberty to form a full close on any note which did not involve too many extraneous sharps or flats for its correct accomplishment. But there was a great difference between modal and modern conceptions of modulation. We have said that the close on the second degree of the Ionian mode was Dorian, but such a modulation was not regarded as a visit paid to the Dorian mode, but merely as the formation of a momentary point of repose on the second degree of the Ionian mode. When therefore it is said that the modulations of 16th-century music are “purposeless and shifting,” the criticism implies a purpose in change of key which is wholly irrelevant. The modal composers’ purpose lay in purely local relationships of harmony, in various degrees of refinement which are often crowded out of the larger and more coarse-grained scheme of modern harmony, but which modern harmony is perfectly capable of employing in precisely the same sense whenever it has leisure.
Modulation, in the modern sense of the term, is a different thing. The modern sense of tonality is so firm, and modern designs so large, that it is desirable that different portions of a composition should be arranged round different harmonic centres or keys, and moreover that the relation between these keys and the primary key should be felt, and the whole design should at last return to the primary key, to remain there with such emphasis and proportion as shall leave upon the mind the impression that the whole is in the primary key and that the foreign keys have been as artistically grouped around it as its own local harmonies. The true principles on which keys are related proved so elastic in the hands of Beethoven that their results utterly outstripped the earlier theory which adhered desperately to the limitations of the 16th century; and so vast is the range of key which Beethoven is able to organize in a convincing scheme of relationship, that even modern theory, dazzled by the true harmonic possibilities, is apt to come to the conclusion, more lame and impotent than any ancient pedantry, that all keys are equally related. A vague conception, dubbed “the unity of the chromatic scale,” is thus made to explain away the whole beauty and power of Wagner’s no less than Beethoven’s harmonic system. We have not space to dispute the matter here, and it must suffice to state dogmatically and statistically the classical facts of key-relationship, including those which Beethoven established as normal possibilities on the suggestion of Haydn, in whose works they appear as special effects.
a. Direct Relationships.—The first principle on which two keys are considered to be related is a strengthening of that which determined the so-called modulations of the 16th-century modes. Two keys are directly related when the tonic chord of the one is among the common chords of the other. Thus, D minor is related to C major because the tonic chord of D minor is the common chord on the supertonic of C (see Ex. 6). In the same way the four other related keys to C major are E minor the mediant, F major the subdominant, G major the dominant and A minor the submediant.
 |
This last key-relationship is sometimes called the “relative” minor, partly because it is usually expressed by the same key-signature as the tonic, but probably more justifiably because it is the point of view from which to reckon the key-relationships of the minor tonic. If we take the minor scale in its “harmonic” form (i.e. the form deducible from its chords of minor tonic, minor subdominant and major dominant, without regard to the exigencies of melody in concession to which the “melodic” minor scale raises the 6th in ascent and flattens the 7th in descent), we shall find it impossible to build a common chord upon its mediant (Ex. 10). But we have seen that A minor is related to C major; therefore it is absurd to suppose that C major is not related to A minor. Clearly then we must deduce some of the relationships of a minor tonic as the converse of those of a major tonic. Thus we may read Ex. 6 backwards and reason as follows: A minor is the submediant of C major; therefore C major is the mediant or relative major of A minor. D minor is the supertonic of C major; therefore C major is related to D minor and may be called its flat 7th. Taking A minor as our standard key, G major is then the flat 7th to A minor. The remaining major keys (C major to E minor = F major to A minor) may be traced directly as well as conversely; and the subdominant, being minor, does not involve an appeal to the major scale at all. But with the dominant we find the curious fact that while the dominant chord of a minor key is major it is impossible to regard the major dominant key as directly related to the minor tonic, since it does not contain the minor tonic chord at all; e.g. the only chord of A in E major is A major. But the dominant minor key contains the tonic chord of the primary minor key clearly enough as subdominant, and therefore when we modulate from a minor tonic to a minor dominant we feel that we have a direct key-relationship and have not lost touch with our tonic. Thus in the minor mode modulation to the dominant key is, though frequent and necessary, a much more uphill process than in the major mode, because the naturally major dominant chord has first to be contradicted. On the other hand, a contrast between minor tonic and major dominant key is very difficult to work on a large scale (as, for example, in the complementary key for second subjects of sonata movements) because, while the major dominant key behaves as if not directly related to the minor tonic, it also gives a curious sensation of being merely on the dominant instead of in it; and thus we find that in the few classical examples of a dominant major second subject in a minor sonata-movement the second subject either relapses into the dominant minor, as in Beethoven’s Kreutzer Sonata and the finale of Brahms’s Third Symphony, or begins in it, as in the first movement of Brahms’s Fourth Symphony.
The effect of a modulation to a related key obviously depends upon the change of meaning in the chords common to both keys, and also in the new chords introduced. Thus, in modulating to the dominant we invest the brightest chord of our first key with the finality and importance of a tonic; our original tonic chord becomes comparatively soft in its new position as subdominant; and a new dominant chord arises, surpassing in brilliance the old dominant (now tonic) as that surpassed the primary tonic. Again, in modulating to the subdominant the softest chord of the primary key becomes tonic, the old tonic is comparatively bright, and a new and softer subdominant chord appears. We have seen the peculiarities of modulation to the dominant from a minor tonic, and it follows from them that modulation from a minor tonic to the subdominant involves the beautiful effect of a momentary conversion of the primary tonic chord to major, the poetic and often dramatically ironical power of which is manifested at the conclusion of more than half the finest classical slow movements in minor keys, from Bach’s E♭ minor Prelude in the first book of the Forty-eight to the slow movement of Brahms’s G major String Quintet, Op. 111.
The effect of the remaining key-relationships involves contrasts between major and minor mode; but it is otherwise far less defined, since the primary tonic chord does not occupy a cardinal position in the second key. These key-relationships are most important from a minor tonic, as the change from minor to major is more vivid than the reverse change. The smoothest changes are those to “relative” minor, “relative” major (C to A minor; C minor to E♭); and mediant minor and submediant major (C to E minor; C minor to A♭). The change from major tonic to supertonic minor is extremely natural on a small scale, i.e. within the compass of a single melody, as may be seen in countless openings of classical sonatas. But on a large scale the identity of primary dominant with secondary subdominant confuses the harmonic perspective, and accordingly in classical music the supertonic minor appears neither in the second subjects of first movements nor as the key for middle movements.[5] But since the key-relationships of a minor tonic are at once more obscure harmonically and more vivid in contrast, we find that the converse key-relationship of the flat 7th, though somewhat bold and archaic in effect on a small scale, has once or twice been given organic function on a large scale in classical movements of exceptionally fantastic character, of which the three great examples are the ghostly slow movement of Beethoven’s D major Trio, Op. 70, No. 1, the scherzo of his Ninth Symphony, and the finale of Brahms’s D minor Violin Sonata (where, however, the C major theme soon passes permanently into the more orthodox dominant minor).
Thus far we have the set of key-relationships universally recognized since the major and minor modes were established, a relationship based entirely on the place of the primary tonic chord in the second key. It only remains for us to protest against the orthodox description of the five related keys as being the “relative” minor or major and the dominant and subdominant with their “relative” minors or majors; a conception which expresses the fallacious assumption that keys which are related to the same key are related to one another, and which thereby implies that all keys are equally related and that classical composers were fools. It cannot be too strongly insisted that there is no foundation for key-relationship except through a tonic, and that it is through the tonic that the most distant keys have always been connected by every composer with a wide range of modulation, from Haydn to Brahms and (with due allowance for the conditions of his musical drama) Wagner.
b. Indirect Relationships.—So strong is the identity of the tonic in major and minor mode that Haydn and Mozart had no scruple in annexing, with certain reservations, the key-relationships of either as an addition to those of the other. The smoothness of Mozart’s style makes him prefer to annex the key-relationships of the tonic minor (e.g. C major to A♭, the submediant of C minor), because the primary tonic note is in the second key, although its chord is transformed. His range of thought does not allow him to use these keys otherwise than episodically; but he certainly does not treat them as chaotically remote by confining them to rapid modulations in the development-portions of his movements. They occur characteristically as beautiful purple patches before or during his second subjects. Haydn, with his mastery of rational paradox, takes every opportunity, in his later works, of using all possible indirect key-relationships in the choice of key for slow movements and for the trios of minuets. By using them thus sectionally (i.e. so as not to involve the organic connecting links necessary for the complementary keys of second subjects) he gives himself a free hand; and he rather prefers those keys which are obtained by transforming the minor relationships of a major primary key (e.g. C to A major instead of A minor). These relationships are of great brilliance and also of some remoteness of effect, since the primary tonic note, as well as its chord, disappears entirely. Haydn also obtains extreme contrasts by changing both modes (e.g. C minor to A major, as in the G minor Quartet, Op. 72, No 6, where the slow movement is in E major), and indeed there is not one key-contrast known to Beethoven and Brahms which Haydn does not use with complete sense of its meaning, though his art admits it only as a surprise.
Beethoven rationalized every step in the whole possible range of key-relationship by such harmonic means as are described in the article Beethoven. Haydn’s favourite key-relationships he used for the complementary key in first movements; and he at once discovered that the use of the major mediant as complementary key to a major tonic implied at all events just as much suggestion of the submediant major in the recapitulation as would not keep the latter half of the movement for too long out of the tonic. The converse is not the case, and where Beethoven uses the submediant major as complementary key in a major first movement he does not subsequently introduce the still more remote and brilliant mediant in the recapitulation. The function of the complementary key is that of contrast and vividness, so that if the key is to be remote it is as well that it should be brilliant rather than sombre; and accordingly the easier key-relationships obtainable through transforming the tonic into minor do not appear as complementary keys until Beethoven’s latest and most subtle works, as the Quartet in B♭, Op. 130 (where we again note that the flat submediant of the exposition is temporarily answered by the flat mediant of the recapitulation).
c. Artificial Key-relationships.—Early in the history of the minor mode it was discovered that the lower tetrachord could be very effectively and naturally altered so as to resemble the upper (thus producing the scale C D♭ E♮ F, G A♭ B♮ C). This produces a flat supertonic (the chord of which is generally presented in its first inversion, and is known as the Neapolitan 6th, from its characteristic use in the works of the Neapolitan school which did so much to establish modern tonality) and its origin, as just described, often impels it to resolve on a major tonic chord. Consequently it exists in the minor mode as a phenomenon not much more artificial than the mode itself; and although the keys it thus connects are extremely remote, and the effect of their connexion very surprising, the connexion is none the less real, whether from a major or a minor tonic, and is a crucial test of a composer’s sense of key-perspective. Thus Philipp Emanuel Bach in a spirit of mere caprice puts the charming little slow movement of his D major Symphony into E♭ and obliterates all real relationship by chaotic operatic connecting links. Haydn’s greatest pianoforte sonata (which, being probably his last, is of course No. 1 in most editions) is in E♭, and its slow movement is in F♮ major (= F♭). That key had already appeared, with surprising effect, in the wanderings of the development of the first movement. No attempt is made to indicate its connexion with E♭; and the finale begins in E♭, but its first bar is unharmonized and starts on the one note which most contradicts E♮ and least prepares the mind for E♭. The immediate repetition of the opening phrase a step higher on the normal supertonic strikes the note which the opening had contradicted, and thus shows its function in the main key without in the least degree explaining away the paradoxical effect of the key of the slow movement. Brahms’s Violoncello Sonata Op. 99, is in F; a prominent episode in the development of the first movement is in E♯ minor (= G♭), thus preparing the mind for the slow movement, which is in F♯ major (= G♭), with a central episode in F minor. The scherzo is in F minor, and begins on the dominant. Thus if we play its first chord immediately after the last chord of the slow movement we have exactly that extreme position of flat supertonic followed by dominant which is a favourite form of cadence in Wagner, who can even convey its meaning by its mere bass without any harmonies (Walküre, Act 3, Scene 2: “Was jetzt du bist, das sage dir selbst”).
Converse harmonic relationships are, as we have seen, always weaker than their direct forms. And thus the relation of C major to B major or minor (as shown in the central episode of the slow movement just mentioned) is rare. Still more rare is the obtaining of indirect artificial relationships, of which the episode in the first movement just mentioned is an illustration in so far as it enhances the effect of the slow movement, but is inconclusive in so far as it is episodic. For with remote key-relationships everything depends upon whether they are used with what may be called cardinal function (like complementary keys) or not. Even a near key may occur in the course of wandering modulations without producing any effect of relationship at all, and this should always be borne in mind whenever we accumulate statistics from classical music.
d. Contrary and Unconnected Keys.—There remain only two pairs of keys that classical music has not brought into connexion, a circumstance which has co-operated with the utter vagueness of orthodox theories on the subject to confirm the conventionally progressive critic in his conviction that all modulations are alike. We have seen how the effect of modulation from major tonic to minor supertonic is, on a large scale, obscured by the identity of the primary dominant with the secondary subdominant, though the one chord is major and the other minor. Now when the supertonic becomes major this difference no longer obviates the confusion, and modulation from C major to D major, though extremely easy, is of so bewildering effect that it is used by classical composers only in moments of intensely dramatic surprise, as, for example, in the recapitulation of the first subject of Beethoven’s Eroica Symphony, and the last variation (or coda) of the slow movement of his Trio in B♭, Op. 97. And in both cases the balance is restored by the converse (and equally if not more contradictory) modulation between major tonic and major flat 7th, though in the slow movement of the B♭ Trio the latter is represented only by its dominant chord which is “enharmonically” resolved into quite another key. The frequent attempts made by easy-going innovators to treat these key-contrasts on another footing than that of paradox, dramatic surprise or hesitation, only show a deficient sense of tonality, which must also mean an inability to see the intensely powerful effect of the true use of such modulations in classical music, an effect which is entirely independent of any ability to formulate a theory to explain it.[6] There now remains only one pair of keys that have never been related, namely, those that (whether major or minor) are at the distance of a tritone 4th. In the first place they are unrelated because there is no means of putting any form of a tonic chord of F♯ into any form of the key of C, or vice versa; and in the second place because it is impossible to tell which of two precisely opposite keys the second key may be (e.g. we have no means of knowing that a direct modulation from C to F♯ is not from C to G♭, which is exactly the same distance in the opposite direction). And this brings us to the only remaining subjects of importance in the science and art of harmony, namely, those of the tempered scale, enharmonic ambiguity and just intonation. Before proceeding we subjoin a table of all the key-relationships from major and minor tonics, representing the degrees by capital Roman figures when the second key is major and small figures when minor. Thus I represents tonic major, iv represents subdominant minor, and so on. A flat or a sharp after the figure indicates that the normal degree of the standard scale has been lowered or raised a semitone, even when in any particular pair of keys it would not be expressed by a flat or a sharp. Thus vi♭ would, from the tonic of B♭ major, express the position of the slow movement of Beethoven’s Sonata, Op. 106, which is written in F♯ minor since G♭ minor is beyond the practical limits of notation.
| TABLES OF KEY-RELATIONSHIPS |
| A. From Major Tonic |
 |
| B. From Minor Tonic 3
|
| 2 Very rare, but the slow movement of Schubert’s C major String Quintet demonstrates it magnificently.
3 All the indirect relationships from a minor tonic are distinctly strained and, except in the violently contrasted doubly indirect keys, obscure as being themselves minor. But the direct artificial modulation is quite smooth, and rich rather than remote. See Beethoven’s C♯ minor Quartet. 4 No classical example, though the clearer converse from a major tonic occurs effectively. 5 Not (with the exception of II) so violent as when from major tonic. Bach, whose range seldom exceeds direct key-relationships, is not afraid to drift from D minor to C minor, though nothing would induce him to go from D major to C major or minor. |
VI. Temperament and Enharmonic Changes.—As the facts of artistic harmony increased in complexity and range, the purely acoustic principles which (as Helmholtz has shown) go so far to explain 16th-century aesthetics became more and more inadequate; and grave practical obstacles to euphonious tuning began to assert themselves. The scientific (or natural) ratios of the diatonic scale were not interfered with by art so long as no discords were “fundamental”; but when discords began to assume independence, one and the same note often became assignable on scientific grounds to two slightly different positions in pitch, or at all events to a position incompatible with even tolerable effect in performance. Thus, the chord of the diminished 7th is said to be intolerably harsh in “just intonation,” that is to say, intonation based upon the exact ratios of a normal minor scale. In practical performance the diminished 7th contains three minor 3rds and two imperfect 5ths (such as that which is present in the dominant 7th), while the peculiarly dissonant interval from which the chord takes its name is very nearly the same as a major 6th. Now it can only be said that an intonation which makes nonsense of chords of which every classical composer from the time of Corelli has made excellent sense, is a very unjust intonation indeed; and to anybody who realizes the universal relation between art and nature it is obvious that the chord of the diminished 7th must owe its naturalness to its close approximation to the natural ratios of the minor scale, while it owes its artistic possibility to the extremely minute instinctive modification by which its dissonance becomes tolerable. As a matter of fact, although we have shown here and in the article Music how artificial is the origin and nature of all but the very scantiest materials of the musical language, there is no art in which the element of practical compromise is so minute and so hard for any but trained scientific observation to perceive. If a painter could have a scale of light and shade as nearly approaching nature as the practical intonation of music approaches the acoustic facts it really involves, a visit to a picture gallery would be a severe strain on the strongest eyes, as Ruskin constantly points out. Yet music is in this respect exactly on the same footing as other arts. It constitutes no exception to the universal law that artistic ideas must be realized, not in spite of, but by means of practical necessities. However independent the treatment of discords, they assert themselves in the long run as transient. They resolve into permanent points of repose of which the basis is natural; but the transient phenomena float through the harmonic world adapting themselves, as best they can, to their environment, showing as much dependence upon the stable scheme of “just intonation” as a crowd of metaphors and abstractions in language shows a dependence upon the rules of the syllogism. As much and no more, but that is no doubt a great deal. Yet the attempt to determine the point in modern harmony where just intonation should end and the tempered scale begin, is as vexatious as the attempt to define in etymology the point at which the literal meaning of a word gives places to a metaphorical meaning. And it is as unsound scientifically as the conviction of the typical circle-squarer that he is unravelling a mystery and measuring a quantity hitherto unknown. Just intonation is a reality in so far as it emphasizes the contrast between concord and discord; but when it forbids artistic interaction between harmony and melody it is a chimera. It is sometimes said that Bach, by the example of his forty-eight preludes and fugues in all the major and minor keys, first fixed the modern scale. This is true practically, but not aesthetically. By writing a series of movements in every key of which the keynote was present in the normal organ and harpsichord manuals of his and later times, he enforced the system by which all facts of modern musical harmony are represented on keyed instruments by dividing the octave into twelve equal semitones, instead of tuning a few much-used keys as accurately as possible and sacrificing the euphony of all the rest. This system of equal temperament, with twelve equal semitones in the octave, obviously annihilates important distinctions, and in the most used keys it sours the concords and blunts the discords more than unequal temperament; but it is never harsh; and where it does not express harmonic subtleties the ear instinctively supplies the interpretation; as the observing faculty, indeed, always does wherever the resources of art indicate more than they express.
Now it frequently happens that discords or artificial chords are not merely obscure in their intonation, whether ideally or practically, but as produced in practice they are capable of two sharply distinct interpretations. And it is possible for music to take advantage of this and to approach a chord in one significance and quit it with another. Where this happens in just intonation (in so far as that represents a real musical conception) such chords will, so to speak, quiver from one meaning into the other. And even in the tempered scale the ear will interpret the change of meaning as involving a minute difference of intonation. The chord of the diminished 7th has in this way four different meanings—
 |
and the chord of the augmented 6th, when accompanied by the fifth, may become a dominant 7th or vice versa, as in the passage already cited in the coda of the slow movement of Beethoven’s B♭ Trio, Op. 97. Such modulations are called enharmonic. We have seen that all the more complex musical phenomena involve distinctions enharmonic in the sense of intervals smaller than a semitone, as, for instance, whenever the progression D E in the scale of C, which is a minor tone, is identified with the progression of D E in the scale of D, which is a major tone (differing from the former as 89 from 910). But the special musical meaning of the word “enharmonic” is restricted to the difference between such pairs of sharps with flats or naturals as can be represented on a keyboard by the same note, this difference being the most impressive to the ear in “just intonation” and to the imagination in the tempered scale.
Not every progression of chords which is, so to speak, spelt enharmonically is an enharmonic modulation in itself. Thus a modulation from D flat to E major looks violently enharmonic on paper, as in the first movement of Beethoven’s Sonata, Op. 110. But E major with four sharps is merely the most convenient way of expressing F flat, a key which would need six flats and a double flat. The reality of an enharmonic modulation can be easily tested by transporting the passage a semitone. Thus, the passage just cited, put a semitone lower, becomes a perfectly diatonic modulation from C to E flat. But no transposition of the sixteen bars before the return of the main theme in the scherzo of Beethoven’s Sonata in E♭, Op. 31, No. 3, will get rid of the fact that the diminished 7th (G B♭ D♭ E♮), on the dominant of F minor, must have changed into G B♭ D♭ F♭ (although Beethoven does not take the trouble to alter the spelling) before it could resolve, as it does, upon the dominant of A♭. But though there is thus a distinction between real and apparent enharmonic modulations, it frequently happens that a series of modulations perfectly diatonic in themselves returns to the original key by a process which can only be called an enharmonic circle. Thus the whole series of keys now in practical use can be arranged in what is called the circle of fifths (C G D A E B F♯ [= G♭] D♭ A♭ B♭ F C, from which series we now see the meaning of what was said in the discussion of key-relationships as to the ambiguity of the relationships between keys a tritone fourth apart). Now no human memory is capable of distinguishing the difference of pitch between the keys of C and B♯ after a wide series of modulations. The difference would be perceptible enough in immediate juxtaposition, but after some interval of time the memory will certainly accept two keys so near in pitch as identical, whether in “just intonation” or not. And hence the enharmonic circle of fifths is a conception of musical harmony by which infinity is at once rationalized and avoided, just as some modern mathematicians are trying to rationalize the infinity of space by a non-Euclidian space so curved in the fourth dimension as to return upon itself. A similar enharmonic circle progressing in major 3rds is of frequent occurrence and of very rich effect. For example, the keys of the movements of Brahms’s C Minor Symphony are C minor, E major, A♭ major (= G♯), and C (= B♯). And the same circle occurs in the opposite direction in the first movement of his Third Symphony, where the first subject is in F, the transition passes directly to D♭ and thence by exactly the same step to A (= B♭♭). The exposition is repeated, which of course means that in “just intonation” the first subject would begin in G♭♭ and then pass through a transition in E♭♭♭ to the second subject in C♭♭♭. As the development contains another spurious enharmonic modulation, and the recapitulation repeats in another position the first spurious enharmonic modulation of the exposition, it would follow that Brahms’s movement began in F and ended in C sextuple-flat! So much, then, for the application of bad metaphysics and circle-squaring mathematics to the art of music. Neither in mathematics nor in art is an approximation to be confused with an imperfection. Brahms’s movement begins and ends in F much more exactly than any wooden diagonal fits a wooden square.
The following series of musical illustrations show the genesis of typical harmonic resources of classical and modern music.
| Ex. 12.—Three concords (ionic, first inversion of subdominant, and dominant of A minor, a possible 16th-century cadence in the Phrygian mode). |  |
| Ex. 13.—The same chords varied by a suspension (*). |  |
| Ex. 14.—Ditto, with the further addition of a double suspension (*) and two passing notes (††). |  |
| Ex. 15.—Ditto, with a chromatic alteration of the second chord (*) and an “essential” discord (dominant 7th) at (†). |  |
| Ex. 16.—Ditto, with chromatic passing notes (**) and appoggiaturas (††). |  |
| Ex. 17.—The last two chords of Ex. 16 attacked unexpectedly, the first appoggiatura (*) prolonged till it seems to make a strange foreign chord before it resolves on the short note at ‡, while the second appoggiatura (†) is chromatic. |  |
| Ex. 18.—The same enharmonically transformed so as to become a variation of the “dominant ninth” of C minor. The G♯ at * is really A♭, and ‡ is no longer a note of resolution, but a chromatic passing-note. |  |
(Intended to comprise the general conceptions set forth in the above article.)
1. Musical sounds, or notes, are sensations produced by regular periodical vibrations in the air, sufficiently rapid to coalesce in a single continuous sensation, and not too rapid for the mechanism of the human ear to respond.
2. The pitch of a note is the sensation corresponding to the degree of rapidity of its vibrations; being low or grave where these are slow, and high or acute where they are rapid.
3. An interval is the difference in pitch between two notes.
4. Rhythm is the organization, in a musical scheme, of sounds in respect of time.
5. Melody is the organization, in a musical scheme, of rhythmic notes in respect of pitch.
6. Harmony is the organization, in a musical scheme, of simultaneous combinations of notes on principles whereby their acoustic properties interact with laws of rhythm and melody.
7. The harmonic series is an infinite series of notes produced by the subdivision of a vibrating body or column of air into aliquot parts, such notes being generally inaudible except in the form of the timbre which their presence in various proportions imparts to the fundamental note produced by the whole vibrating body or air-column.
8. A concord is a combination which, both by its acoustic smoothness and by its logical origin and purpose in a musical scheme, can form a point of repose.
9. A discord is a combination in which both its logical origin in a musical scheme and its acoustic roughness show that it cannot form a point of repose.
10. The perfect concords and perfect intervals are those comprised within the first four members of the harmonic series, namely, the octave, as between numbers 1 and 2 of the series (see Ex. 1 above); the 5th, as between Nos. 2 and 3; and the 4th, as between Nos. 3 and 4.
11. All notes exactly one or more octaves apart are regarded as harmonically identical.
12. The root of a chord is that note from which the whole or the most important parts of the chord appear (if distributed in the right octaves) as members of the harmonic series.
13. A chord is inverted when its lowest note is not its root.
14. The major triad is a concord containing three different notes which (octaves being disregarded) are identical with the first, third and fifth members of the harmonic series (the second and fourth members being negligible as octaves).
15. The minor triad is a concord containing the same intervals as the major triad in a different order; in consequence it is artificial, as one of its notes is not derivable from the harmonic series.
16. Unessential discords are those that are treated purely as the phenomena of transition, delay or ornament, in an otherwise concordant harmony.
17. Essential discords are those which are so treated that the mind tends to regard them as definite chords possessing roots.
18. A key is an harmonic system in which there is never any doubt as to which note or triad shall be the final note of music in that system, nor of the relations between that note or chord and the other notes or chords. (In this sense the church modes are either not keys or else they are subtle mixtures of keys.)
19. This final note of a key is called its tonic.
20. The major mode is that of keys in which the tonic triad and the two other cardinal triads are major.
21. The minor mode is that of keys in which the tonic triad and one other cardinal triad are minor.
22. A diatonic scale is a series of the notes essential to one major or minor key, arranged in order of pitch and repeating itself in other octaves on reaching the limit of an octave.
23. Modulation is the passing from one key to another.
24. Chromatic notes and chords are those which do not belong to the diatonic scale of the passage in which they occur, but which are not so used as to cause modulation.
25. Enharmonic intervals are minute intervals which never occur in music as directly measured quantities, though they exist as differences between approximately equal ordinary intervals, diatonic or chromatic. In an enharmonic modulation, two chords differing by an enharmonic quantity are treated as identical.
26. Pedal or organ point is the sustaining of a single note in the bass (or, in the case of an inverted pedal, in an upper part) while the harmonies move independently. Unless the harmonies are sometimes foreign to the sustained note, it does not constitute a pedal. In modern music pedals take place on either the tonic or the dominant, other pedal-notes being rare and of complex meaning. Double pedals (of tonic and dominant, with tonic below) are not unusual. The device is capable of very free treatment, and has produced many very bold and rich harmonic effects in music since the earlier works of Beethoven. It probably accounts for many so-called “essential discords.”
In the form of drones the pedal is the only real harmonic device of ancient and primitive music. The ancient Greeks sometimes used a reiterated instrumental note as an accompaniment above the melody. These primitive devices, though harmonic in the true modern sense of the word, are out of the line of harmonic development, and did not help it in any definite way.
27. The fundamental bass of a harmonic passage is an imaginary bass consisting of the roots of the chords.
28. A figured bass, or continuo, is the bass of a composition supplied with numerals indicating the chords to be filled in by the accompanist. Thorough-bass (Ger. Generalbass) is the art of interpreting such figures. (D. F. T.)
- ↑ Musical intervals are reckoned numerically upwards along the degrees of the diatonic scales (described below). Intervals greater than an octave are called compound, and are referred to their simple forms, e.g. the 12th is a compound 5th.
- ↑ It is at least probable that this is one of the several rather obscure reasons for the peculiar instability of the 4th in modern harmony, which is not yet satisfactorily explained.
- ↑ The perfect concords are the octave, unison, 5th and 4th. Other diatonic combinations, whether concords or discords, are called imperfect.
- ↑ See Plain Song.
- ↑ Until Beethoven developed the resources for a wider scheme of key-contrasts, the only keys for second subjects of sonata-movements were the dominant (when the tonic was major) and the “relative” major or dominant minor (when the tonic was minor). A wider range was possible only in the irresponsible style of D. Scarlatti.
- ↑ Many theorists mistake the usual extreme emphasis on the dominant chord of the dominant key, in preparation for second subjects, for a modulation to the major supertonic, but this can deceive no one with any sense of tonality. A good practical test is to see what becomes of such passages when translated into the minor mode. Illusory modulation to the flat 7th frequently occurs as a bold method of throwing strong emphasis on to the subdominant at the outset of a movement, as in Beethoven’s Sonata, Op. 31, No. 1.
