CIRCLE (from the Lat. circulus, the diminutive of circus, a
ring; the cognate Gr. word is κιρκος, generally used in the form
κρίκος), a plane curve definable as the locus of a point which
moves so that its distance from a fixed point is constant.
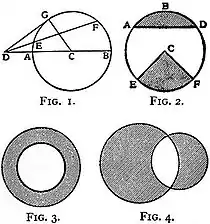
The form of a circle is familiar to all; and we proceed to define certain lines, points, &c., which constantly occur in studying its geometry. The fixed point in the preceding definition is termed the “centre” (C in fig. 1); the constant distance, e.g. CG, the “radius.” The curve itself is sometimes termed the “circumference.” Any line through the centre and terminated at both extremities by the curve, e.g. AB, is a “diameter”; any other line similarly terminated, e.g. EF, a “chord.” Any line drawn from an external point to cut the circle in two points, e.g. DEF, is termed a “secant”; if it touches the circle, e.g. DG, it is a “tangent.” Any portion of the circumference terminated by two points, e.g. AD (fig. 2), is termed an “arc”; and the plane figure enclosed by a chord and arc, e.g. ABD, is termed a “segment”; if the chord be a diameter, the segment is termed a “semicircle.” The figure included by two radii and an arc is a “sector,” e.g. ECF (fig. 2). “Concentric circles” are, as the name obviously shows, circles having the same centre; the figure enclosed by the circumferences of two concentric circles is an “annulus” (fig. 3), and of two non-concentric circles a “lune,” the shaded portions in fig. 4; the clear figure is sometimes termed a “lens.”
The circle was undoubtedly known to the early civilizations, its simplicity specially recommending it as an object for study. Euclid defines it (Book I. def. 15) as a “plane figure enclosed by one line, all the straight lines drawn to which from one point within the figure are equal to one another.” In the succeeding three definitions the centre, diameter and the semicircle are defined, while the third postulate of the same book demands the possibility of describing a circle for every “centre” and “distance.” Having employed the circle for the construction and demonstration of several propositions in Books I. and II. Euclid devotes his third book entirely to theorems and problems relating to the circle, and certain lines and angles, which he defines in introducing the propositions. The fourth book deals with the circle in its relations to inscribed and circumscribed triangles, quadrilaterals and regular polygons. Reference should be made to the article Geometry: Euclidean, for a detailed summary of the Euclidean treatment, and the elementary properties of the circle.
In the article Geometry: Analytical, it is shown that the general equation to a circle in rectangular Cartesian co-ordinates is x2+y2+2gx+2fy+c=0, i.e. in the general equation of the second degree the co-efficients of x2 and y2 are Cartesian co-ordinates. equal, and of xy zero. The co-ordinates of its centre are –g/c, –f/c; and its radius is (g2+f 2–c)12. The equations to the chord, tangent and normal are readily derived by the ordinary methods.
Consider the two circles:—
Obviously these equations show that the curves intersect in four points, two of which lie on the intersection of the line, 2(g – g′)x + 2(f – f ′)y + c – c′ = 0, the radical axis, with the circles, and the other two where the lines x2 + y2 = (x + iy) (x – iy) = 0 (where i = √–1) intersect the circles. The first pair of intersections may be either real or imaginary; we proceed to discuss the second pair.
The equation x2 + y2 = 0 denotes a pair of perpendicular imaginary lines; it follows, therefore, that circles always intersect in two imaginary points at infinity along these lines, and since the terms x2 + y2 occur in the equation of every circle, it is seen that all circles pass through two fixed points at infinity. The introduction of these lines and points constitutes a striking achievement in geometry, and from their association with circles they have been named the “circular lines” and “circular points.” Other names for the circular lines are “circulars” or “isotropic lines.” Since the equation to a circle of zero radius is x2 + y2 = 0, i.e. identical with the circular lines, it follows that this circle consists of a real point and the two imaginary lines; conversely, the circular lines are both a pair of lines and a circle. A further deduction from the principle of continuity follows by considering the intersections of concentric circles. The equations to such circles may be expressed in the form x2 + y2 = α2, x2 + y2 = β2. These equations show that the circles touch where they intersect the lines x2 + y2 = 0, i.e. concentric circles have double contact at the circular points, the chord of contact being the line at infinity.
In various systems of triangular co-ordinates the equations to circles specially related to the triangle of reference assume comparatively simple forms; consequently they provide elegant algebraical demonstrations of properties concerning a triangle and the circles intimately associated with its geometry. In this article the equations to the more important circles—the circumscribed, inscribed, escribed, self-conjugate—will be given; reference should be made to the article Triangle for the consideration of other circles (nine-point, Brocard, Lemoine, &c.); while in the article Geometry: Analytical, the principles of the different systems are discussed.
The equation to the circumcircle assumes the simple form aβγ + bγα + cαβ = 0, the centre being cos A, cos B, cos C. The inscribed circle is cos 12A √α cos 12B √β + cos 12C √γ = 0, with centre α = β = γ; while the escribed circle opposite the angle A Trilinear co-ordinates. is cos 12A √–α + sin 12B √β + sin 12C √γ = 0, with centre -α = β = γ. The self-conjugate circle is α2 sin 2A + β2 sin 2B + γ2 sin 2C = 0, or the equivalent form a cosA α2 + b cos B β2 + c cos C γ2 = 0, the centre being sec A, sec B, sec C.
The general equation to the circle in trilinear co-ordinates is readily deduced from the fact that the circle is the only curve which intersects the line infinity in the circular points. Consider the equation
| aβγ + bγα + Cαβ + (lα + mβ + nγ) (aα + bβ + cγ) = 0 | (1). |
This obviously represents a conic intersecting the circle aβγ + bγα + cαβ = 0 in points on the common chords lα + mβ + nγ = 0, aα + bβ + cγ = 0. The line lα + mβ + nγ is the radical axis, and since aα + bβ + cγ = 0 is the line infinity, it is obvious that equation (1) represents a conic passing through the circular points, i.e. a circle. If we compare (1) with the general equation of the second degree uα2 + vβ2 + wγ2 + 2u′βγ + 2v′γα + 2w′αβ = 0, it is readily seen that for this equation to represent a circle we must have
The corresponding equations in areal co-ordinates are readily derived by substituting x/a, y/b, z/c for α, β, γ respectively in the trilinear equations. The circumcircle is thus seen to be a2yz + b2zx + c2xy = 0, with centre sin 2A, sin 2B, Areal co-ordinates.sin 2C; the inscribed circle is √(x cot 12A) + √(y cot 12B) + √(z cot 12C) = 0, with centre sin A, sin B, sin C; the escribed circle opposite the angle A is √(–x cot 12A) + √(y tan 12B) + √(z tan 12C)=0, with centre – sin A, sin B, sin C; and the self-conjugate circle is x2 cot A + y2 cot B + z2 cot C = 0, with centre tan A, tan B, tan C. Since in areal co-ordinates the line infinity is represented by the equation x + y + z = 0 it is seen that every circle is of the form a2yz + b2zx + c2xy + (lx + my + nz)(x + y + z) = 0. Comparing this equation with ux2 + vy2 + wz2 + 2u′yz + 2v′zx + 2w′xy = 0, we obtain as the condition for the general equation of the second degree to represent a circle:—
In tangential (p, q, r) co-ordinates the inscribed circle has for its equation (s – a)qr + (s – b)rp + (s – c)pq = 0, s being equal to 12(a + b + c); an alternative form is qr cot 12A + rp cot 12B + pq cot 12C = 0; the centre is ap + bq + cr = 0, or p sin A + q sin B + r sin C = 0. Tangential co-ordinates.The escribed circle opposite the angle A is –sqr + (s – c)rp + (s – b)pq = 0 or –qr cot 12A + rp tan 12B + pq tan 12C = 0, with centre –ap + bq + cr = 0. The circumcircle is a √(p) + b √(q) + c √(r) = 0, the centre being p sin 2A + q sin 2B + r sin 2C = 0. The general equation to a circle in this system of co-ordinates is deduced as follows: If ρ be the radius and lp + mq + nr = 0 the centre, we have ρ=(lp1–mq1+nr1)/(l+m+n), in which p1, q1, r1 is a line distant ρ from the point lp+mq+nr=0. Making this equation homogeneous by the relation Σa2(p−q) (p−r) = 4Δ2 (see Geometry: Analytical), which is generally written {ap, bq, cr}2 = 4Δ2, we obtain {ap, bq, cr}2ρ2 = 4Δ2 {(lp+mq+nr)/(l+m+n)}2, the accents being dropped, and p, q, r regarded as current co-ordinates. This equation, which may be more conveniently written {ap, bq, cr}2 = (λp + μq + νr)2, obviously represents a circle, the centre being λp+μq+νr=0, and radius 2Δ/(λ + μ + ν). If we make λ = μ = ν = 0, ρ is infinite, and we obtain {ap, bq, cr}2=0 as the equation to the circular points.
Centres and Circle of Similitude.—The “centres of similitude” of two circles may be defined as the intersections of the common tangents to the two circles, the direct common tangents giving rise to the “external centre,” the transverse tangents to the “internal centre.” It may be readily shown that the external and internal centres are the points where the line joining the centres of the two circles is divided externally and internally in the ratio of their radii.
The circle on the line joining the internal and external centres of similitude as diameter is named the “circle of similitude.” It may be shown to be the locus of the vertex of the triangle which has for its base the distance between the centres of the circles and the ratio of the remaining sides equal to the ratio of the radii of the two circles.
With a system of three circles it is readily seen that there are six centres of similitude, viz. two for each pair of circles, and it may be shown that these lie three by three on four lines, named the “axes of similitude.” The collinear centres are the three sets of one external and two internal centres, and the three external centres.
Coaxal Circles.—A system of circles is coaxal when the locus of points from which tangents to the circles are equal is a straight line. Consider the case of two circles, and in the first place suppose them to intersect in two real points A and B. Then by Euclid iii. 36 it is seen that the line joining the points A and B is the locus of the intersection of equal tangents, for if P be any point on AB and PC and PD the tangents to the circles, then PA·PB = PC2 = PD2, and therefore PC = PD. Furthermore it is seen that AB is perpendicular to the line joining the centres, and divides it in the ratio of the squares of the radii. The line AB is termed the “radical axis.” A system coaxal with the two given circles is readily constructed by describing circles through the common points on the radical axis and any third point; the minimum circle of the system is obviously that which has the common chord of intersection for diameter, the maximum is the radical axis—considered as a circle of infinite radius. In the case of two non-intersecting circles it may be shown that the radical axis has the same metrical relations to the line of centres.
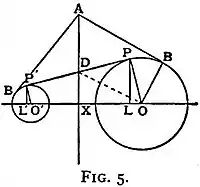
There are several methods of constructing the radical axis in this case. One of the simplest is: Let P and P′ (fig. 5) be the points of contact of a common tangent; drop perpendiculars PL, P′L′, from P and P′ to OO′, the line joining the centres, then the radical axis bisects LL′ (at X) and is perpendicular to OO′. To prove this let AB, AB¹ be the tangents from any point on the line AX. Then by Euc. i. 47, AB2=AO2–OB2=AX2+OX2+OP2; and OX2=OD2–DX2=OP2+PD2–DX2. Therefore AB2=AX2–DX2+PD2. Similarly AB′2=AX2–DX2+DP′2. Since PD=PD′, it follows that AB=AB′.
To construct circles coaxal with the two given circles, draw the tangent, say XR, from X, the point where the radical axis intersects the line of centres, to one of the given circles, and with centre X and radius XR describe a circle. Then circles having the intersections of tangents to this circle and the line of centres for centres, and the lengths of the tangents as radii, are members of the coaxal system.
In the case of non-intersecting circles, it is seen that the minimum circles of the coaxal system are a pair of points I and I′, where the orthogonal circle to the system intersects the line of centres; these points are named the “limiting points.” In the case of a coaxal system having real points of intersection the limiting points are imaginary. Analytically, the Cartesian equation to a coaxal system can be written in the form x2+y2+2ax±k2=0, where a varies from member to member, while k is a constant. The radical axis is x = 0, and it may be shown that the length of the tangent from a point (0, h) is h2 ± k2, i.e. it is independent of a, and therefore of any particular member of the system. The circles intersect in real or imaginary points according to the lower or upper sign of k2, and the limiting points are real for the upper sign and imaginary for the lower sign. The fundamental properties of coaxal systems may be summarized:—
1. The centres of circles forming a coaxal system are collinear;
2. A coaxal system having real points of intersection has imaginary limiting points;
3. A coaxal system having imaginary points of intersection has real limiting points;
4. Every circle through the limiting points cuts all circles of the system orthogonally;
5. The limiting points are inverse points for every circle of the system.
The theory of centres of similitude and coaxal circles affords elegant demonstrations of the famous problem: To describe a circle to touch three given circles. This problem, also termed the “Apollonian problem,” was demonstrated with the aid of conic sections by Apollonius in his book on Contacts or Tangencies; geometrical solutions involving the conic sections were also given by Adrianus Romanus, Vieta, Newton and others. The earliest analytical solution appears to have been given by the princess Elizabeth, a pupil of Descartes and daughter of Frederick V. John Casey, professor of mathematics at the Catholic university of Dublin, has given elementary demonstrations founded on the theory of similitude and coaxal circles which are reproduced in his Sequel to Euclid; an analytical solution by Gergonne is given in Salmon’s Conic Sections. Here we may notice that there are eight circles which solve the problem.
All exact relations pertaining to the mensuration of the circle involve the ratio of the circumference to the diameter. This ratio, invariably denoted by π, is constant for all circles, but it does not admit of exact arithmetical expression, being of the nature of an incommensurable number. Very early in the history of geometry it was known that the circumference and area of a circle of radius r could be expressed in the forms 2πr and πr2. The exact geometrical evaluation of the second quantity, viz. πr2, which, in reality, is equivalent to determining a square equal in area to a circle, engaged the attention of mathematicians for many centuries. The history of these attempts, together with modern contributions to our knowledge of the value and nature of the number π, is given below (Squaring of the Circle).
The following table gives the values of this constant and several expressions involving it:—
| Number. | Logarithm. | Number. | Logarithm. | ||
| π | 3.1415927 | 0.4971499 | π2 | 9.8696044 | 0.9942997 |
| 2π | 6.2831858 | 0.7981799 | |||
| 4π | 12.5663706 | 1.0992099 | 16π2 | 0.0168869 | 2.2275490 |
| 12π | 1.5707963 | 0.1961199 | |||
| 13π | 1.0471976 | 0.0200286 | √π | 1.7724539 | 0.2485750 |
| 14π | 0.7853982 | 1.8950899 | |||
| 16π | 0.5235988 | 1.7189986 | ∛π | 1.4645919 | 0.1657166 |
| 18π | 0.3926991 | 1.5940599 | |||
| 112π | 0.2617994 | 1.4179686 | 1√π | 0.5641896 | 1.7514251 |
| 43π | 4.1887902 | 0.6220886 | |||
| π180 | 0.0174533 | 2.2418774 | 2√π | 1.1283792 | 0.0524551 |
| 1π | 0.3183099 | 1.5028501 | 12√π | 0.2820948 | 1.4503951 |
| 4π | 1.2732395 | 0.1049101 | ∛(6π) | 0.2820948 | 1.4503951 |
| 14π | 0.0795775 | 2.9097901 | ∛(34π) | 0.6203505 | 1.7926371 |
| 180π | 57.2957795 | 1.7581226 | loge π | 1.1447299 | 0.0587030 |
Useful fractional approximations are 22/7 and 355/113.
A synopsis of the leading formula connected with the circle will now be given.
1. Circle.—Data: radius = a. Circumference = 2πa. Area = πa2.
2. Arc and Sector.—Data: radius = a; θ = circular measure of angle subtended at centre by arc; c = chord of arc; c2 = chord of semi-arc; c4 = chord of quarter-arc.
Exact formulae are:—Arc = aθ, where θ may be given directly, or indirectly by the relation c=2a sin 12θ. Area of sector = 12a2θ = 12 radius × arc.
Approximate formulae are:—Arc = 13(8c2 − c) (Huygen’s formula); arc = 145(c − 40c2 + 256c4).
3. Segment.—Data: a, θ, c, c2, as in (2); h = height of segment, i.e. distance of mid-point of arc from chord.
Exact formulae are:—Area = 12a2(θ − sin θ) = 12a2θ − 14c2 cot 12θ = 12a2 − 12c √(a2 − 14c2). If h be given, we can use c2 + 4h2 = 8ah, 2h = c tan 14θ to determine θ.
Approximate formulae are:—Area = 115(6c + 8c2)h; = 23 √(c2 + 8/5h2)·h; = 115(7c + 3α)h, α being the true length of the arc.
From these results the mensuration of any figure bounded by circular arcs and straight lines can be determined, e.g. the area of a lune or meniscus is expressible as the difference or sum of two segments, and the circumference as the sum of two arcs. (C. E.*)
Squaring of the Circle.
The problem of finding a square equal in area to a given circle, like all problems, may be increased in difficulty by the imposition of restrictions; consequently under the designation there may be embraced quite a variety of geometrical problems. It has to be noted, however, that, when the “squaring” of the circle is especially spoken of, it is almost always tacitly assumed that the restrictions are those of the Euclidean geometry.
Since the area of a circle equals that of the rectilineal triangle whose base has the same length as the circumference and whose altitude equals the radius (Archimedes, Κύκλου μέτρησις, prop. 1), it follows that, if a straight line could be drawn equal in length to the circumference, the required square could be found by an ordinary Euclidean construction; also, it is evident that, conversely, if a square equal in area to the circle could be obtained it would be possible to draw a straight line equal to the circumference. Rectification and quadrature of the circle have thus been, since the time of Archimedes at least, practically identical problems. Again, since the circumferences of circles are proportional to their diameters—a proposition assumed to be true from the dawn almost of practical geometry—the rectification of the circle is seen to be transformable into finding the ratio of the circumference to the diameter. This correlative numerical problem and the two purely geometrical problems are inseparably connected historically.
Probably the earliest value for the ratio was 3. It was so among the Jews (1 Kings vii. 23, 26), the Babylonians (Oppert, Journ. asiatique, August 1872, October 1874), the Chinese (Biot, Journ. asiatique, June 1841), and probably also the Greeks. Among the ancient Egyptians, as would appear from a calculation in the Rhind papyrus, the number (43)4, i.e. 3.1605, was at one time in use.[1] The first attempts to solve the purely geometrical problem appear to have been made by the Greeks (Anaxagoras, &c.)[2], one of whom, Hippocrates, doubtless raised hopes of a solution by his quadrature of the so-called meniscoi or lune.[3]
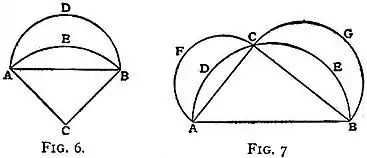
[The Greeks were in possession of several relations pertaining to the quadrature of the lune. The following are among the more interesting. In fig. 6, ABC is an isosceles triangle right angled at C, ADB is the semicircle described on AB as diameter, AEB the circular arc described with centre C and radius CA = CB. It is easily shown that the areas of the lune ADBEA and the triangle ABC are equal. In fig. 7, ABC is any triangle right angled at C, semicircles are described on the three sides, thus forming two lunes AFCDA and CGBEC. The sum of the areas of these lunes equals the area of the triangle ABC.]
As for Euclid, it is sufficient to recall the facts that the original author of prop. 8 of book iv. had strict proof of the ratio being < 4, and the author of prop. 15 of the ratio being > 3, and to direct attention to the importance of book x. on incommensurables and props. 2 and 16 of book xii., viz. that “circles are to one another as the squares on their diameters” and that “in the greater of two concentric circles a regular 2n-gon can be inscribed which shall not meet the circumference of the less,” however nearly equal the circles may be.
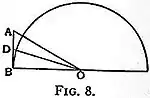
With Archimedes (287–212 B.C.) a notable advance was made. Taking the circumference as intermediate between the perimeters of the inscribed and the circumscribed regular n-gons, he showed that, the radius of the circle being given and the perimeter of some particular circumscribed regular polygon obtainable, the perimeter of the circumscribed regular polygon of double the number of sides could be calculated; that the like was true of the inscribed polygons; and that consequently a means was thus afforded of approximating to the circumference of the circle. As a matter of fact, he started with a semi-side AB of a circumscribed regular hexagon meeting the circle in B (see fig. 8), joined A and B with O the centre, bisected the angle AOB by OD, so that BD became the semi-side of a circumscribed regular 12-gon; then as AB:BO:OA::1: √3:2 he sought an approximation to √3 and found that AB:BO > 153:265. Next he applied his theorem[4] BO + OA:AB::OB:BD to calculate BD; from this in turn he calculated the semi-sides of the circumscribed regular 24-gon, 48-gon and 96-gon, and so finally established for the circumscribed regular 96-gon that perimeter:diameter < 317:1. In a quite analogous manner he proved for the inscribed regular 96-gon that perimeter:diameter > 31071:1. The conclusion from these therefore was that the ratio of circumference to diameter is < 317 and > 31071. This is a most notable piece of work; the immature condition of arithmetic at the time was the only real obstacle preventing the evaluation of the ratio to any degree of accuracy whatever.[5]
No advance of any importance was made upon the achievement of Archimedes until after the revival of learning. His immediate successors may have used his method to attain a greater degree of accuracy, but there is very little evidence pointing in this direction. Ptolemy (fl. 127–151), in the Great Syntaxis, gives 3.141552 as the ratio[6]; and the Hindus (c. A.D. 500), who were very probably indebted to the Greeks, used 62832/20000, that is, the now familiar 3.1416.[7]
It was not until the 15th century that attention in Europe began to be once more directed to the subject, and after the resuscitation a considerable length of time elapsed before any progress was made. The first advance in accuracy was due to a certain Adrian, son of Anthony, a native of Metz (1527), and father of the better-known Adrian Metius of Alkmaar. In refutation of Duchesne(Van der Eycke), he showed that the ratio was < 317120 and > 315106, and thence made the exceedingly lucky step of taking a mean between the two by the quite unjustifiable process of halving the sum of the two numerators for a new numerator and halving the sum of the two denominators for a new denominator, thus arriving at the now well-known approximation 316113 or 335113, which, being equal to 3.1415929. . ., is correct to the sixth fractional place.[8]
The next to advance the calculation was Francisco Vieta. By finding the perimeter of the inscribed and that of the circumscribed regular polygon of 393216 (i.e. 6 × 216) sides, he proved that the ratio was > 3.1415926535 and < 3.1415926537, so that its value became known (in 1579) correctly to 10 fractional places. The theorem for angle-bisection which Vieta used was not that of Archimedes, but that which would now appear in the form 1 − cos θ = 2 sin2 12θ. With Vieta, by reason of the advance in arithmetic, the style of treatment becomes more strictly trigonometrical; indeed, the Universales Inspectiones, in which the calculation occurs, would now be called plane and spherical trigonometry, and the accompanying Canon mathematicus a table of sines, tangents and secants.[9] Further, in comparing the labours of Archimedes and Vieta, the effect of increased power of symbolical expression is very noticeable. Archimedes’s process of unending cycles of arithmetical operations could at best have been expressed in his time by a “rule” in words; in the 16th century it could be condensed into a “formula.” Accordingly, we find in Vieta a formula for the ratio of diameter to circumference, viz. the interminate product[10]—
From this point onwards, therefore, no knowledge whatever of geometry was necessary in any one who aspired to determine the ratio to any required degree of accuracy; the problem being reduced to an arithmetical computation. Thus in connexion with the subject a genus of workers became possible who may be styled “π-computers or circle-squarers”—a name which, if it connotes anything uncomplimentary, does so because of the almost entirely fruitless character of their labours. Passing over Adriaan van Roomen (Adrianus Romanus) of Louvain, who published the value of the ratio correct to 15 places in his Idea mathematica (1593),[11] we come to the notable computer Ludolph van Ceulen (d. 1610), a native of Germany, long resident in Holland. His book, Van den Circkel (Delft, 1596), gave the ratio correct to 20 places, but he continued his calculations as long as he lived, and his best result was published on his tombstone in St Peter’s church, Leiden. The inscription, which is not known to be now in existence,[12] is in part as follows:—
. . . . Qui in vita sua multo labore circumferentiae circuli proximam rationem ad diametrum invenit sequentem—
| quando diameter est 1 | |
| tum circuli circumferentia plus est | |
| quam | 314159265358979323846264338327950288 |
| 100000000000000000000000000000000000 | |
| et minus | |
| quam | 314159265358979323846264338327950289 |
| 100000000000000000000000000000000000 . . . | |
This gives the ratio correct to 35 places. Van Ceulen’s process was essentially identical with that of Vieta. Its numerous root extractions amply justify a stronger expression than “multo labore,” especially in an epitaph. In Germany the “Ludolphische Zahl” (Ludolph’s number) is still a common name for the ratio.[13]
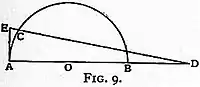
Up to this point the credit of most that had been done may be set down to Archimedes. A new departure, however, was made by Willebrord Snell of Leiden in his Cyclometria, published in 1621. His achievement was a closely approximate geometrical solution of the problem of rectification (see fig. 9): ACB being a semicircle whose centre is O, and AC the arc to be rectified, he produced AB to D, making BD equal to the radius, joined DC, and produced it to meet the tangent at A in E; and then his assertion (not established by him) was that AE was nearly equal to the arc AC, the error being in defect. For the purposes of the calculator a solution erring in excess was also required, and this Snell gave by slightly varying the former construction. Instead of producing AB (see fig. 10) so that BD was
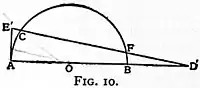
equal to r, he produced it only so far that, when the extremity D′ was joined with C, the part D′F outside the circle was equal to r; in other words, by a non-Euclidean construction he trisected the angle AOC, for it is readily seen that, since FD′ = FO = OC, the angle FOB = 13AOC.[14] This couplet of constructions is as important from the calculator’s point of view as it is interesting geometrically. To compare it on this score with the fundamental proposition of Archimedes, the latter must be put into a form similar to Snell’s. AMC being an arc of a circle (see fig. 11) whose centre is O, AC its chord, and HK the tangent drawn at the middle point of the arc and bounded by OA, OC produced, then, according to Archimedes, AMC < HK, but > AC. In modern trigonometrical notation the propositions to be compared stand as follows:—
| 2 tan 12θ > θ > 2 sin 12θ | (Archimedes); |
| tan 13θ + 2 sin 13θ > θ > 3 sin θ2 + cos θ | (Snell). |
It is readily shown that the latter gives the best approximation to θ; but, while the former requires for its application a knowledge of the trigonometrical ratios of only one angle (in other words, the ratios of the sides of only one right-angled triangle), the latter requires the same for two angles, θ and 13θ.
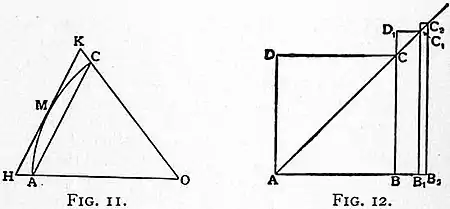
Grienberger, using Snell’s method, calculated the ratio correct to 39 fractional places.[15] C. Huygens, in his De Circuli Magnitudine Inventa, 1654, proved the propositions of Snell, giving at the same time a number of other interesting theorems, for example, two inequalities which may be written as follows[16]—
As might be expected, a fresh view of the matter was taken by René Descartes. The problem he set himself was the exact converse of that of Archimedes. A given straight line being viewed as equal in length to the circumference of a circle, he sought to find the diameter of the circle. His construction is as follows (see fig. 12). Take AB equal to one-fourth of the given line; on AB describe a square ABCD; join AC; in AC produced find, by a known process, a point C1 such that, when C1B1 is drawn perpendicular to AB produced and C1D1 perpendicular to BC produced, the rectangle BC1 will be equal to 14ABCD; by the same process find a point C2 such that the rectangle B1C2 will be equal to 14BC1; and so on ad infinitum. The diameter sought is the straight line from A to the limiting position of the series of B’s, say the straight line AB∞. As in the case of the process of Archimedes, we may direct our attention either to the infinite series of geometrical operations or to the corresponding infinite series of arithmetical operations. Denoting the number of units in AB by 14c, we can express BB1, B1B2, . . . in terms of 14c, and the identity AB∞ = AB + BB1 + B1B2 + . . . gives us at once an expression for the diameter in terms of the circumference by means of an infinite series.[17] The proof of the correctness of the construction is seen to be involved in the following theorem, which serves likewise to throw new light on the subject:—AB being any straight line whatever, and the above construction being made, then AB is the diameter of the circle circumscribed by the square ABCD (self-evident), AB1 is the diameter of the circle circumscribed by the regular 8-gon having the same perimeter as the square, AB2 is the diameter of the circle circumscribed by the regular 16-gon having the same perimeter as the square, and so on. Essentially, therefore, Descartes’s process is that known later as the process of isoperimeters, and often attributed wholly to Schwab.[18]
In 1655 appeared the Arithmetica Infinitorum of John Wallis, where numerous problems of quadrature are dealt with, the curves being now represented in Cartesian co-ordinates, and algebra playing an important part. In a very curious manner, by viewing the circle y = (1 − x2)12 as a member of the series of curves y = (1 − x2)1, y = (1 − x2)2, &c., he was led to the proposition that four times the reciprocal of the ratio of the circumference to the diameter, i.e. 4/π, is equal to the infinite product
3 · 3 · 5 · 5 · 7 · 7 · 9 . . .2 · 4 · 4 · 6 · 6 · 8 · 8 . . . ;
and, the result having been communicated to Lord Brounker, the latter discovered the equally curious equivalent continued fraction
1 + 122
+ 322
+ 522
+ 722 . . .
The work of Wallis had evidently an important influence on the next notable personality in the history of the subject, James Gregory, who lived during the period when the higher algebraic analysis was coming into power, and whose genius helped materially to develop it. He had, however, in a certain sense one eye fixed on the past and the other towards the future. His first contribution[19] was a variation of the method of Archimedes. The latter, as we know, calculated the perimeters of successive polygons, passing from one polygon to another of double the number of sides; in a similar manner Gregory calculated the areas. The general theorems which enabled him to do this, after a start had been made, are
A′2n = 2An A′nAn + A′2n or 2A′n A2nA′n + A2n (Gregory),
where An, A′n are the areas of the inscribed and the circumscribed regular n-gons respectively. He also gave approximate rectifications of circular arcs after the manner of Huygens; and, what is very notable, he made an ingenious and, according to J. E. Montucla, successful attempt to show that quadrature of the circle by a Euclidean construction was impossible.[20] Besides all this, however, and far beyond it in importance, was his use of infinite series. This merit he shares with his contemporaries N. Mercator, Sir I. Newton and G. W. Leibnitz, and the exact dates of discovery are a little uncertain. As far as the circle-squaring functions are concerned, it would seem that Gregory was the first (in 1670) to make known the series for the arc in terms of the tangent, the series for the tangent in terms of the arc, and the secant in terms of the arc; and in 1669 Newton showed to Isaac Barrow a little treatise in manuscript containing the series for the arc in terms of the sine, for the sine in terms of the arc, and for the cosine in terms of the arc. These discoveries formed an epoch in the history of mathematics generally, and had, of course, a marked influence on after investigations regarding circle-quadrature. Even among the mere computers the series
θ = tan − 13 tan3 θ + 15 tan5 θ − . . .,
specially known as Gregory’s series, has ever since been a necessity of their calling.
The calculator’s work having now become easier and more mechanical, calculation went on apace. In 1699 Abraham Sharp, on the suggestion of Edmund Halley, took Gregory’s series, and, putting tan θ = 13√3, found the ratio equal to
from which he calculated it correct to 71 fractional places.[21] About the same time John Machin calculated it correct to 100 places, and, what was of more importance, gave for the ratio the rapidly converging expression
which long remained without explanation.[22] Fautet de Lagny, still using tan 30°, advanced to the 127th place.[23]
Leonhard Euler took up the subject several times during his life, effecting mainly improvements in the theory of the various series.[24] With him, apparently, began the usage of denoting by π the ratio of the circumference to the diameter.[25]
The most important publication, however, on the subject in the 18th century was a paper by J. H. Lambert,[26] read before the Berlin Academy in 1761, in which he demonstrated the irrationality of π. The general test of irrationality which he established is that, if
a1b1 ± a2b2 ± a3b3 ± . . .
be an interminate continued fraction, a1, a2, . . ., b1, b2 . . . be integers, a1/b1, a2/b2, . . . be proper fractions, and the value of every one of the interminate continued fractions
a1b1 ± . . .,a2b2 ± . . ., . . . be < 1, then the given continued fraction represents an irrational quantity. If this be applied to the right-hand side of the identity
tan mn = mn – m23n – m25n . . .
it follows that the tangent of every arc commensurable with the radius is irrational, so that, as a particular case, an arc of 45°, having its tangent rational, must be incommensurable with the radius; that is to say, π/4 is an incommensurable number.[27]
This incontestable result had no effect, apparently, in repressing the π-computers. G. von Vega in 1789, using series like Machin’s, viz. Gregory’s series and the identities
π/4 = 5 tan–1 17 + 2 tan–1 {379 (Euler, 1779),
π/4 = tan–1 17 + 2 tan–1 13 (Hutton, 1776),
neither of which was nearly so advantageous as several found by Charles Hutton, calculated π correct to 136 places.[28] This achievement was anticipated or outdone by an unknown calculator, whose manuscript was seen in the Radcliffe library, Oxford, by Baron von Zach towards the end of the century, and contained the ratio correct to 152 places. More astonishing still have been the deeds of the π-computers of the 19th century. A condensed record compiled by J. W. L. Glaisher (Messenger of Math. ii. 122) is as follows:—
| Date. | Computer. | No. of fr. digits calcd. |
No. of fr. digits correct. |
Place of Publication. |
| 1842 | Rutherford | 208 | 152 | Trans. Roy. Soc. (London, 1841), p. 283. |
| 1844 | Dase | 205 | 200 | Crelle’s Journ.. xxvii. 198. |
| 1847 | Clausen | 250 | 248 | Astron. Nachr. xxv. col. 207. |
| 1853 | Shanks | 318 | 318 | Proc. Roy. Soc. (London, 1853), 273. |
| 1853 | Rutherford | 440 | 440 | Ibid. |
| 1853 | Shanks | 530 | .. | Ibid. |
| 1853 | Shanks | 607 | .. | W. Shanks, Rectification of the Circle (London, 1853). |
| 1853 | Richter | 333 | 330 | Grunert’s Archiv, xxi. 119. |
| 1854 | Richter | 400 | 330 | Ibid. xxii. 473. |
| 1854 | Richter | 400 | 400 | Ibid. xxiii. 476. |
| 1854 | Richter | 500 | 500 | Ibid. xxv. 472. |
| 1873 | Shanks | 707 | .. | Proc. Roy. Soc. (London), xxi. |
By these computers Machin’s identity, or identities analogous to it, e.g.
π/4 = 4tan–1 15 − tan–1 170 + tan–1 199 (Rutherford),
and Gregory’s series were employed.[29]
A much less wise class than the π-computers of modern times are the pseudo-circle-squarers, or circle-squarers technically so called, that is to say, persons who, having obtained by illegitimate means a Euclidean construction for the quadrature or a finitely expressible value for π, insist on using faulty reasoning and defective mathematics to establish their assertions. Such persons have flourished at all times in the history of mathematics; but the interest attaching to them is more psychological than mathematical.[30]
It is of recent years that the most important advances in the theory of circle-quadrature have been made. In 1873 Charles Hermite proved that the base η of the Napierian logarithms cannot be a root of a rational algebraical equation of any degree.[31] To prove the same proposition regarding π is to prove that a Euclidean construction for circle-quadrature is impossible. For in such a construction every point of the figure is obtained by the intersection of two straight lines, a straight line and a circle, or two circles; and as this implies that, when a unit of length is introduced, numbers employed, and the problem transformed into one of algebraic geometry, the equations to be solved can only be of the first or second degree, it follows that the equation to which we must be finally led is a rational equation of even degree. Hermite[32] did not succeed in his attempt on π; but in 1882 F. Lindemann, following exactly in Hermite’s steps, accomplished the desired result.[33] (See also Trigonometry.)
References.—Besides the various writings mentioned, see for the history of the subject F. Rudio, Geschichte des Problems von der Quadratur des Zirkels (1892); M. Cantor, Geschichte der Mathematik (1894–1901); Montucla, Hist. des. math. (6 vols., Paris, 1758, 2nd ed. 1799–1802); Murhard, Bibliotheca Mathematica, ii. 106-123 (Leipzig, 1798); Reuss, Repertorium Comment. vii. 42-44 (Göttingen, 1808). For a few approximate geometrical solutions, see Leybourn’s Math. Repository, vi. 151-154; Grunert’s Archiv, xii. 98, xlix. 3; Nieuw Archief v. Wisk. iv. 200-204. For experimental determinations of π, dependent on the theory of probability, see Mess. of Math. ii. 113, 119; Casopis pro pĭstování math. a fys. x. 272-275; Analyst, ix. 176. (T. Mu.)
- ↑ Eisenlohr, Ein math. Handbuch d. alten Ägypter, übers. u. erklärt (Leipzig, 1877); Rodet, Bull. de la Soc. Math. de France, vi. pp. 139-149.
- ↑ H. Hankel, Zur Gesch. d. Math. im Alterthum, &c., chap, v (Leipzig, 1874); M. Cantor, Vorlesungen über Gesch. d. Math. i. (Leipzig, 1880); Tannery, Mém. de la Soc., &c., à Bordeaux; Allman, in Hermathena.
- ↑ Tannery. Bull. des sc. math. [2], x. pp. 213-226.
- ↑ In modern trigonometrical notation, 1 + sec θ:tan θ::1:tan 12θ.
- ↑ Tannery, “Sur la mesure du cercle d’Archimède,” in Mém. . ..Bordeaux[2], iv. pp. 313-339; Menge, Des Archimedes Kreismessung (Coblenz, 1874).
- ↑ De Morgan, in Penny Cyclop, xix. p. 186.
- ↑ Kern, Aryabhattíyam (Leiden, 1874), trans. by Rodet (Paris,1879).
- ↑ De Morgan, art. “Quadrature of the Circle,” in English Cyclop.; Glaisher, Mess. of Math. ii. pp. 119-128, iii. pp. 27-46; de Haan, Nieuw Archief v. Wisk. i. pp. 70-86, 206-211.
- ↑ Vieta, Opera math. (Leiden, 1646); Marie, Hist. des sciences math. iii. 27 seq. (Paris, 1884).
- ↑ Klügel, Math. Wörterb. ii. 606, 607.
- ↑ Kästner, Gesch. d. Math. i. (Göttingen, 1796–1800).
- ↑ But see Les Délices de Leide (Leiden, 1712); or de Haan, Mess. of Math. iii. 24-26.
- ↑ For minute and lengthy details regarding the quadrature of the circle in the Low Countries, see de Haan, “Bouwstoffen voor de geschiedenis, &c.,” in Versl. en Mededeel. der K. Akad. van Wetensch. ix., x., xi., xii. (Amsterdam); also his “Notice sur quelques quadrateurs, &c.,” in Bull. di bibliogr. e di storia delle sci. mat. e fis. vii. 99-144.
- ↑ It is thus manifest that by his first construction Snell gave an approximate solution of two great problems of antiquity.
- ↑ Elementa trigonometrica (Rome, 1630); Glaisher, Messenger of Math. iii. 35 seq.
- ↑ See Kiessling’s edition of the De Circ. Magn. Inv. (Flensburg, 1869); or Pirie’s tract on Geometrical Methods of Approx. to the Value of π (London, 1877).
- ↑ See Euler, “Annotationes in locum quendam Cartesii,” in Nov. Comm. Acad. Petrop. viii.
- ↑ Gergonne, Annales de math. vi.
- ↑ See Vera Circuli et Hyperbolae Quadratura (Padua, 1667); and the Appendicula to the same in his Exercitationes geometricae (London, 1668).
- ↑ Penny Cyclop. xix. 187.
- ↑ See Sherwin’s Math. Tables (London, 1705), p. 59.
- ↑ See W. Jones, Synopsis Palmariorum Matheseos (London, 1706); Maseres, Scriptores Logarithmici (London, 1791–1796), iii. 159 seq.; Hutton, Tracts, i. 266.
- ↑ See Hist. de l’Acad. (Paris, 1719); 7 appears instead of 8 in the 113th place.
- ↑ Comment. Acad. Petrop. ix., xi.; Nov. Comm. Ac. Pet. xvi.; Nova Acta Acad. Pet. xi.
- ↑ Introd. in Analysin Infin. (Lausanne, 1748), chap. viii.
- ↑ Mém. sur quelques propriétés remarquables des quantités transcendantes, circulaires, et logarithmiques.
- ↑ See Legendre, Eléments de géométrie (Paris, 1794), note iv.; Schlömilch, Handbuch d. algeb. Analysis (Jena, 1851), chap. xiii.
- ↑ Nova Acta Petrop. ix. 41; Thesaurus Logarithm. Completus, 633.
- ↑ On the calculations made before Shanks, see Lehmann, “Beitrag zur Berechnung der Zahl π,” in Grunert’s Archiv, xxi. 121-174.
- ↑ See Montucla, Hist. des rech. sur la quad. du cercle (Paris, 1754, 2nd ed. 1831); de Morgan, Budget of Paradoxes (London, 1872).
- ↑ “Sur la fonction exponentielle,” Comples rendus (Paris), lxxvii. 18, 74, 226, 285.
- ↑ See Crelle’s Journal, lxxvi. 342.
- ↑ See “Über die Zahl π,” in Math. Ann. xx. 213.