Straining Actions and Working Stresses.
17. In metal bridges wrought iron has been replaced by mild steel—a stronger, tougher and better material. Ingot metal or mild steel was sometimes treacherous when first introduced, and accidents occurred, the causes of which were obscure. In fact, small differences of composition or variations in thermal treatment during manufacture involve relatively large differences of quality. Now it is understood that care must be taken in specifying the exact quality and in testing the material supplied. Structural wrought iron has a tenacity of 20 to 2212 tons per sq. in. in the direction of rolling, and an ultimate elongation of 8 or 10% in 8 in. Across the direction of rolling the tenacity is about 18 tons per sq. in., and the elongation 3% in 8 in. Steel has only a small difference of quality in different directions. There is still controversy as to what degree of hardness, or (which is nearly the same thing) what percentage of carbon, can be permitted with safety in steel for structures.
The qualities of steel used may be classified as follows:—(a) Soft steel, having a tenacity of 2212 to 26 tons per sq. in., and an elongation of 32 to 24% in 8 in. (b) Medium steel, having a tenacity of 26 to 34 tons per sq. in., and 28 to 25% elongation. (c) Moderately hard steel, having a tenacity of 34 to 37 tons per sq. in., and 17% elongation, (d) Hard steel, having a tenacity of 37 to 40 tons per sq. in., and 10% elongation. Soft steel is used for rivets always, and sometimes for the whole superstructure of a bridge, but medium steel more generally for the plates, angle bars, &c., the weight of the bridge being then reduced by about 7% for a given factor of safety. Moderately hard steel has been used for the larger members of long-span bridges. Hard steel, if used at all, is used only for compression members, in which there is less risk of flaws extending than in tension members. With medium or moderately hard steel all rivet holes should be drilled, or punched ⅛ in. less in diameter than the rivet and reamed out, so as to remove the ring of material strained by the punch.
In the specification for bridge material, drawn up by the British Engineering Standards Committee, it is provided that the steel shall be acid or basic open-hearth steel, containing not more than 0.06% of sulphur or phosphorus. Plates, angles and bars, other than rivet bars, must have a tensile strength of 28 to 32 tons per sq. in., with an elevation of 20% in 8 in. Rivet bars tested on a gauge length eight times the diameter must have a tensile strength of 26 to 30 tons per sq. in. and an elongation of 25%.
18. Straining Actions.—The external forces acting on a bridge may be classified as follows:—
(1) The live or temporary load, for road bridges the weight of a dense crowd uniformly distributed, or the weight of a heavy wagon or traction engine; for railway bridges the weight of the heaviest train likely to come on the bridge. (2) An allowance is sometimes made for impact, that is the dynamical action of the live load due to want of vertical balance in the moving parts of locomotives, to irregularities of the permanent way, or to yielding of the structure. (3) The dead load comprises the weight of the main girders, flooring and wind bracing, or the total weight of the superstructure exclusive of any part directly carried by the piers. This is usually treated as uniformly distributed over the span. (4) The horizontal pressure due to a wind blowing transversely to the span, which becomes of importance in long and high bridges. (5) The longitudinal drag due to the friction of a train when braked, about one-seventh of the weight of the train. (6) On a curved bridge the centrifugal load due to the radical acceleration of the train. If w is the weight of a locomotive in tons, r the radius of curvature of the track, v the velocity in feet per sec.; then the horizontal force exerted on the bridge is wv2/gr tons. (7) In some cases, especially in arch and suspension bridges, changes of temperature set up stresses equivalent to those produced by an external load. In Europe a variation of temperature of 70° C. or 126° F. is commonly assumed. For this the expansion is about 1 in. in 100 ft. Generally a structure should be anchored at one point and free to move if possible in other directions. Roughly, if expansion is prevented, a stress of one ton per sq. in. is set up in steel structures for each 12° change of temperature.
i. Live Load on Road Bridges.—A dense crowd of people may be taken as a uniform load of 80 to 120 ℔ per sq. ft. But in recent times the weight of traction engines and wagons which pass over bridges has increased, and this kind of load generally produces greater straining action than a crowd of people. In manufacturing districts and near large towns loads of 30 tons may come on road bridges, and county and borough authorities insist on provision being made for such loads. In Switzerland roads are divided into three classes according to their importance, and the following loads are prescribed, the designer having to provide sufficient strength either for a uniformly distributed crowd, or for a heavy wagon anywhere on the roadway:—
| Crowd, ℔ per sq. ft. | Wagon, tons per axle. | |
| Main Roads | 92 | 10 with 13 ft. wheel base |
| Secondary Roads | 72 | 6 with 10 ft. wheel base |
| Other Roads | 51 | 3 with 8 ft. wheel base |
In England still larger loads are now provided for. J. C. Inglis (Proc. Inst. C.E. cxli. p. 35) has considered two cases—(a) a traction engine and boiler trolley, and (b) a traction engine and trucks loaded with granite. He has calculated the equivalent load per foot of span which would produce the same maximum bending moments. The following are some of the results:—
| Span Ft. | 10. | 20. | 30. | 40. | 50. |
| Equivalent load in tons per ft. run, Case a | 1.75 | 0.95 | 0.70 | 0.73 | 0.72 |
| Do. Case b | 3.25 | 1.7 | 1.3 | 1.2 | 1.15 |
Large as these loads are on short spans, they are not more than must often be provided for.
Live Load on Railway Bridges.—The live load is the weight of the heaviest train which can come on the bridge. In the earlier girder bridges the live load was taken to be equivalent to a uniform load of 1 ton per foot run for each line of way. At that time locomotives on railways of 4 ft. 812 in. gauge weighed at most 35 to 45 tons, and their length between buffers was such that the average load did not exceed 1 ton per foot run. Trains of wagons did not weigh more than three-quarters of a ton per foot run when most heavily loaded. The weights of engines and wagons are now greater, and in addition it is recognized that the concentration of the loading at the axles gives rise to greater straining action, especially in short bridges, than the same load uniformly distributed along the span. Hence many of the earlier bridges have had to be strengthened to carry modern traffic. The following examples of some of the heaviest locomotives on English railways is given by W. B. Farr (Proc. Inst. C.E. cxli. p. 12):—
| Total weights, tons | 84.35 | 98.90 | 91.90 | 85.48 |
| Tons per ft. over all | 1.58 | 1.71 | 1.62 | 1.61 |
| Tons per ft. of wheel base | 1.92 | 2.04 | 1.97 | 1.95 |
| Maximum axle load, tons | 19.00 | 16.00 | 18.70 | 18.50 |
| Total weight, tons | 77.90 | 78.80 | 76.46 | 75.65 |
| Tons per ft. over all | 1.54 | 1.50 | 1.54 | 1.51 |
| Tons per ft. of wheel base | 2.02 | 2.02 | 2.03 | 2.00 |
| Maximum axle load, tons | 15.90 | 16.00 | 13.65 | 15.50 |
| Total weight, tons | 53.80 | 58.61 | 60.80 | 47.00 |
| Tons per ft. over all | 1.60 | 1.68 | 1.70 | 1.55 |
| Tons per ft. of wheel base | 2.45 | 2.52 | 2.23 | 3.03 |
| Maximum axle load, tons | 17.54 | 15.29 | 17.10 | 15.77 |
Farr has drawn diagrams of bending moment for forty different very heavy locomotives on different spans, and has determined for each case a uniform load which at every point would produce as great a bending moment as the actual wheel loads. The following short abstract gives the equivalent uniform load which produces bending moments as great as those of any of the engines calculated:—
| Span in Ft. | Load per ft. run equivalent to actual Wheel Loads in Tons, for each Track. |
| 5.0 | 7.6 |
| 10.0 | 4.85 |
| 20.0 | 3.20 |
| 30.0 | 2.63 |
| 50.0 | 2.24 |
| 100.0 | 1.97 |
Fig. 36 gives the loads per axle and the distribution of loads in some exceptionally heavy modern British locomotives.
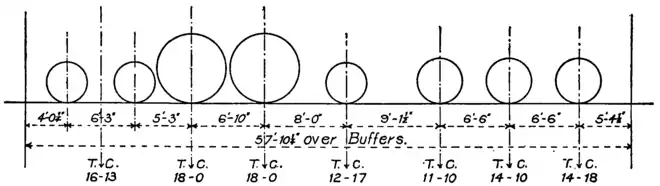
Express Passenger Engine, G. N. Ry.
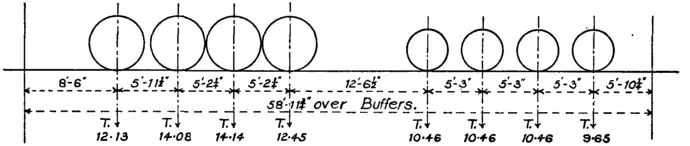
Goods Engine, L. & Y. Ry.
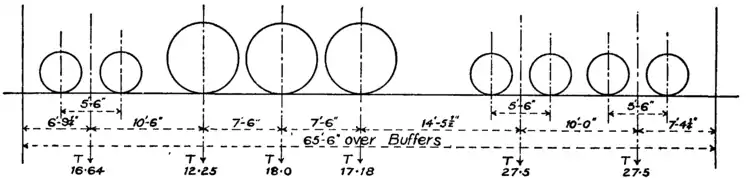
Passenger Engine, Cal. Ry.
Fig. 36.
In Austria the official regulations require that railway bridges shall be designed for at least the following live loads per foot run and per track:—
| Span. | Live Load in Tons. | ||
| Metres. | Ft. | Per metre run. | Per ft. run. |
| 1 | 3.3 | 20 | 6.1 |
| 2 | 6.6 | 15 | 4.6 |
| 5 | 16.4 | 10 | 3.1 |
| 20 | 65.6 | 5 | 1.5 |
| 30 | 98.4 | 4 | 1.2 |
It would be simpler and more convenient in designing short bridges if, instead of assuming an equivalent uniform rolling load, agreement could be come to as to a typical heavy locomotive which would produce stresses as great as any existing locomotive on each class of railway. Bridges would then be designed for these selected loads, and the process would be safer in dealing with flooring girders and shearing forces than the assumption of a uniform load.
Some American locomotives are very heavy. Thus a consolidation engine may weigh 126 tons with a length over buffers of 57 ft., corresponding to an average load of 2.55 tons per ft. run. Also long ore wagons are used which weigh loaded two tons per ft. run. J. A. L. Waddell (De Pontibus, New York, 1898) proposes to arrange railways in seven classes, according to the live loads which may be expected from the character of their traffic, and to construct bridges in accordance with this classification. For the lightest class, he takes a locomotive and tender of 93.5 tons, 52 ft. between buffers (average load 1.8 tons per ft. run), and for the heaviest a locomotive and tender weighing 144.5 tons, 52 ft. between buffers (average load 2.77 tons per ft. run). Wagons he assumes to weigh for the lightest class 1.3 tons per ft. run and for the heaviest 1.9 tons. He takes as the live load for a bridge two such engines, followed by a train of wagons covering the span. Waddell’s tons are short tons of 2000 ℔.
ii. Impact.—If a vertical load is imposed suddenly, but without velocity, work is done during deflection, and the deformation and stress are momentarily double those due to the same load at rest on the structure. No load of exactly this kind is ever applied to a bridge. But if a load is so applied that the deflection increases with speed, the stress is greater than that due to a very gradually applied load, and vibrations about a mean position are set up. The rails not being absolutely straight and smooth, centrifugal and lurching actions occur which alter the distribution of the loading. Again, rapidly changing forces, due to the moving parts of the engine which are unbalanced vertically, act on the bridge; and, lastly, inequalities of level at the rail ends give rise to shocks. For all these reasons the stresses due to the live load are greater than those due to the same load resting quietly on the bridge. This increment is larger on the flooring girders than on the main ones, and on short main girders than on long ones. The impact stresses depend so much on local conditions that it is difficult to fix what allowance should be made. E. H. Stone (Trans. Am. Soc. of C.E. xli. p. 467) collated some measurements of deflection taken during official trials of Indian bridges, and found the increment of deflection due to impact to depend on the ratio of dead to live load. By plotting and averaging he obtained the following results:—
| Dead load in per cent of total load | 10 | 20 | 30 | 40 | 50 | 70 | 90 |
| Live load in per cent of total load | 90 | 80 | 70 | 60 | 50 | 30 | 10 |
| Ratio of live to dead load | 9 | 4 | 2.3 | 1.5 | 1.0 | 0.43 | 0.10 |
| Excess of deflection and stress due to moving load per cent | 23 | 13 | 8 | 5.5 | 4.0 | 1.6 | 0.3 |
These results are for the centre deflections of main girders, but Stone infers that the augmentation of stress for any member, due to causes included in impact allowance, will be the same percentage for the same ratios of live to dead load stresses. Valuable measurements of the deformations of girders and tension members due to moving trains have been made by S. W. Robinson (Trans. Am. Soc. C.E. xvi.) and by F. E. Turneaure (Trans. Am. Soc. C.E. xli.). The latter used a recording deflectometer and two recording extensometers. The observations are difficult, and the inertia of the instrument is liable to cause error, but much care was taken. The most striking conclusions from the results are that the locomotive balance weights have a large effect in causing vibration, and next, that in certain cases the vibrations are cumulative, reaching a value greater than that due to any single impact action. Generally: (1) At speeds less than 25 m. an hour there is not much vibration. (2) The increase of deflection due to impact at 40 or 50 m. an hour is likely to reach 40 to 50% for girder spans of less than 50 ft. (3) This percentage decreases rapidly for longer spans, becoming about 25% for 75-ft. spans. (4) The increase per cent of boom stresses due to impact is about the same as that of deflection; that in web bracing bars is rather greater. (5) Speed of train produces no effect on the mean deflection, but only on the magnitude of the vibrations.
A purely empirical allowance for impact stresses has been proposed, amounting to 20% of the live load stresses for floor stringers; 15% for floor cross girders; and for main girders, 10% for 40-ft. spans, and 5% for 100-ft. spans. These percentages are added to the live load stresses.
iii. Dead Load.—The dead load consists of the weight of main girders, flooring and wind-bracing. It is generally reckoned to be uniformly distributed, but in large spans the distribution of weight in the main girders should be calculated and taken into account. The weight of the bridge flooring depends on the type adopted. Road bridges vary so much in the character of the flooring that no general rule can be given. In railway bridges the weight of sleepers, rails, &c., is 0.2 to 0.25 tons per ft. run for each line of way, while the rail girders, cross girders, &c., weigh 0.15 to 0.2 tons. If a footway is added about 0.4 ton per ft. run may be allowed for this. The weight of main girders increases with the span, and there is for any type of bridge a limiting span beyond which the dead load stresses exceed the assigned limit of working stress.
Let Wl be the total live load, Wf the total flooring load on a bridge of span l, both being considered for the present purpose to be uniform per ft. run. Let k(Wl+Wf) be the weight of main girders designed to carry Wl+Wf, but not their own weight in addition. Then
Wg = (Wl+Wf)(k+k2+k3 ...)
will be the weight of main girders to carry Wl+Wf and their own weight (Buck, Proc. Inst. C.E. lxvii. p. 331). Hence,
Wg = (Wl+Wf)k/(1−k).
Since in designing a bridge Wl+Wf is known, k(Wl+Wf) can be found from a provisional design in which the weight Wg is neglected. The actual bridge must have the section of all members greater than those in the provisional design in the ratio k/(1−k).
Waddell (De Pontibus) gives the following convenient empirical relations. Let w1, w2 be the weights of main girders per ft. run for a live load p per ft. run and spans l1, l2. Then
w2/w1 = 12 [l2/l1+(l2/l1)2].
Now let w1′, w2′ be the girder weights per ft. run for spans l1, l2, and live loads p′ per ft. run. Then
w2′/w2 = 15(1+4p′/p)
w2′/w1 = 110[l2/l1+(l2/l1)2](1+4p′/p)
A partially rational approximate formula for the weight of main girders is the following (Unwin, Wrought Iron Bridges and Roofs, 1869, p. 40):—
Let w = total live load per ft. run of girder; w2 the weight of platform per ft. run; w3 the weight of main girders per ft. run, all in tons; l = span in ft.; s = average stress in tons per sq. in. on gross section of metal; d = depth of girder at centre in ft.; r = ratio of span to depth of girder so that r = l/d. Then
w3 = (w1+w2)l2/(Cds−l2) = (w1+w2)lr/(Cs−lr),
where C is a constant for any type of girder. It is not easy to fix the average stress s per sq. in. of gross section. Hence the formula is more useful in the form
w = (w1+w2)l2/(Kd−l2) = (w1+w2)lr/(K−lr)
where K = (w1+w2+w3)lr/w3 is to be deduced from the data of some bridge previously designed with the same working stresses. From some known examples, C varies from 1500 to 1800 for iron braced parallel or bowstring girders, and from 1200 to 1500 for similar girders of steel. K = 6000 to 7200 for iron and = 7200 to 9000 for steel bridges.
iv. Wind Pressure.—Much attention has been given to wind action since the disaster to the Tay bridge in 1879. As to the maximum wind pressure on small plates normal to the wind, there is not much doubt. Anemometer observations show that pressures of 30 ℔ per sq. ft. occur in storms annually in many localities, and that occasionally higher pressures are recorded in exposed positions. Thus at Bidstone, Liverpool, where the gauge has an exceptional exposure, a pressure of 80 ℔ per sq. ft. has been observed. In tornadoes, such as that at St Louis in 1896, it has been calculated, from the stability of structures overturned, that pressures of 45 to 90 ℔ per sq. ft. must have been reached. As to anemometer pressures, it should be observed that the recorded pressure is made up of a positive front and negative (vacuum) back pressure, but in structures the latter must be absent or only partially developed. Great difference of opinion exists as to whether on large surfaces the average pressure per sq. ft. is as great as on small surfaces, such as anemometer plates. The experiments of Sir B. Baker at the Forth bridge showed that on a surface 30 ft. ✕ 15 ft. the intensity of pressure was less than on a similarly exposed anemometer plate. In the case of bridges there is the further difficulty that some surfaces partially shield other surfaces; one girder, for instance, shields the girder behind it (see Brit. Assoc. Report, 1884). In 1881 a committee of the Board of Trade decided that the maximum wind pressure on a vertical surface in Great Britain should be assumed in designing structures to be 56 ℔ per sq. ft. For a plate girder bridge of less height than the train, the wind is to be taken to act on a surface equal to the projected area of one girder and the exposed part of a train covering the bridge. In the case of braced girder bridges, the wind pressure is taken as acting on a continuous surface extending from the rails to the top of the carriages, plus the vertical projected area of so much of one girder as is exposed above the train or below the rails. In addition, an allowance is made for pressure on the leeward girder according to a scale. The committee recommended that a factor of safety of 4 should be taken for wind stresses. For safety against overturning they considered a factor of 2 sufficient. In the case of bridges not subject to Board of Trade inspection, the allowance for wind pressure varies in different cases. C. Shaler Smith allows 300 ℔ per ft. run for the pressure on the side of a train, and in addition 30 ℔ per sq. ft. on twice the vertical projected area of one girder, treating the pressure on the train as a travelling load. In the case of bridges of less than 50 ft. span he also provides strength to resist a pressure of 50 ℔ per sq. ft. on twice the vertical projection of one truss, no train being supposed to be on the bridge.