Heaviside function
The Heaviside function, often written as H(x), is a non-continuous function whose value is zero for a negative input and one for a positive input.
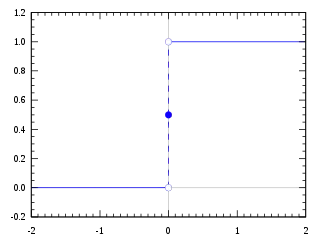
The function is used in the mathematics of control theory to represent a signal that switches on at a specified time, and which stays switched on indefinitely. It was named after the Englishman Oliver Heaviside.
The Heaviside function is the integral of the Dirac delta function: H′(x) = δ(x). This is sometimes written as[1]
Discrete form
We can also define an alternative form of the Heaviside step function as a function of a discrete variable n:
where n is an integer.
Or
The discrete-time unit impulse is the first difference of the discrete-time step
This function is the cumulative summation of the Kronecker delta:
where
is the discrete unit impulse function.
H(0)
The value of the function at 0 can be defined as H(0) = 0, H(0) = ½ or H(0) = 1. In particular:[2]
Related pages
- Laplace transform
- Step function
References
- "List of Calculus and Analysis Symbols". Math Vault. 2020-05-11. Retrieved 2020-10-06.
- Weisstein, Eric W. "Heaviside Step Function". mathworld.wolfram.com. Retrieved 2020-10-06.