Angle
When two straight lines come together, they make an angle. The two lines are called the sides[1] of the angle, and they meet at a point. A flat surface (called a plane) also forms an angle when it meets another.

To represent an angle, Greek letters such as (alpha), (beta), (gamma) and (theta) are sometimes used.[2] An angle indicates the space between its sides, or the amount of rotation needed to make one side coincide the other.[3][4]
To measure the size of an angle, we use units called degrees. A degree is a standard unit and we use the symbol ° after a number to show that it is a number of degrees. We can use a decimal number or a fraction for part of a degree, but a degree can also be divided into 60 minutes (1° = 60'), and a minute can be divided into 60 seconds (1' = 60"). So 22.5°, 221⁄2° and 22° 30' are all the same angle.
In mathematics, angles can also be (and often are) measured in radians instead of degrees, by using the conversion factor (for example, ). Yet another unit of angle is gradian,[4] with .
Angles are studied in geometry, where an angle where edges meet is often called a vertex. For example, the three sides of a triangle are its edges and two of the edges meet at each vertex. Similarly, two of the six sides (or faces) of a cube meet at each of its twelve edges, and three edges meet at each of its eight corners (or vertices, which is the plural version of vertex).
Types of angles
Individual angles
- In a zero angle the lines lie one upon the other thus creating a 0° angle aka the zero angle.
- An angle measuring greater (wider) than 0° but less (narrower) than 90° is called an acute angle.
- An angle 90° wide is called a right angle.
- An angle more than 90° but less than 180° is called an obtuse angle.
- An angle that measures 180° is called a straight angle.
- An angle wider than 180° and narrower than 360° is called a reflex angle.
- An angle that has a made or full circle/completed 360° is called a full or complete angle.[5]
Special angle pairs
In geometry, there are pairs angles having a special relationship with each other, making them interesting and convenient.
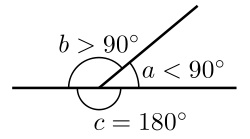
There is a pair of angles called complementary angles to which the sum of their measure (wideness) is equal to one right angle (which is equal to turn, 90°, or radians). Supplementary angles are also two angles, this time their combined measure is a straight angle ( turn, 180°, or radians). Two angles that total to a full angle ( turn, 360°, or radians) are referred to as explementary or conjugate angles.
Related pages
References
- Campana, D. M. (2016-09-06). The Teacher of Geometrical Drawing - For High Schools, Manual Training Schools, Technical Schools, Etc. Read Books Ltd. ISBN 978-1-4733-5366-4.
- "Compendium of Mathematical Symbols". Math Vault. 2020-03-01. Retrieved 2020-08-17.
- "Definition of angle | Dictionary.com". www.dictionary.com. Retrieved 2020-08-17.
- Weisstein, Eric W. "Angle". mathworld.wolfram.com. Retrieved 2020-08-17.
- "Angles - Acute, Obtuse, Straight and Right". www.mathsisfun.com. Retrieved 2020-08-17.