| Truncated tetrahedral prism | |
|---|---|
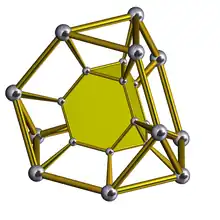 Schlegel diagram | |
| Type | Prismatic uniform polychoron |
| Uniform index | 49 |
| Schläfli symbol | t{3,3}×{} |
| Coxeter-Dynkin | |
| Cells | 10: 2 4 4 |
| Faces | 24: 8 {3} + 18 {4} + 8 {6} |
| Edges | 48 |
| Vertices | 24 |
| Vertex figure |  Isosceles-triangular pyramid |
| Symmetry group | [3,3,2], order 48 |
| Properties | convex |
In geometry, a truncated tetrahedral prism is a convex uniform polychoron (four-dimensional polytope). This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.
It is one of 18 uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids and Archimedean solids.
Alternative names
- Truncated-tetrahedral dyadic prism (Norman W. Johnson)
- Tuttip (Jonathan Bowers: for truncated-tetrahedral prism)
- Truncated tetrahedral hyperprism
External links
- 6. Convex uniform prismatic polychora - Model 49, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) x x3x3o - tuttip".
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
